基于λ-最大相容类的粗糙规划模型及其在企业战略联盟形成决策问题中的应用

关 菲 , 张 强, 栗 军

(1.北京理工大学 管理与经济学院，北京 100081; 2.国网石家庄供电分公司，河北 石家庄 050000)



基于λ-最大相容类的粗糙规划模型及其在企业战略联盟形成决策问题中的应用

关 菲1, 张 强1, 栗 军2

(1.北京理工大学 管理与经济学院，北京 100081; 2.国网石家庄供电分公司，河北 石家庄 050000)

企业战略联盟作为一种新型、双赢的商业竞争模式，近年来，其联盟的形成问题一直是学术界与应用领域广泛关注的研究内容。本文在分析影响企业战略联盟形成的各因素基础上，首先利用序关系G1法对各影响因素指标进行了权重确定，并用基于相似度的聚类分析法来对属性权重进行筛选和修正；其次以形成的联盟稳定性最高为目标，以λ-最大相容类模拟联盟中各企业之间的相似关系，利用粗糙规划模型的性质和特点，建立了基于λ-最大相容类的粗糙规划模型；最后结合企业战略联盟的具体实例，分析了该模型的特点和有效性。结果表明，该模型丰富了现有的理论成果，为战略联盟的有效形成提供了正确的决策参考。

企业战略联盟；联盟形成；最大相容类；粗糙规划模型

0 引言

随着经济全球化和知识经济时代的到来，整个工业生产市场竞争呈现出明显的国际化和一体化趋势，导致了市场竞争的逐步激烈。然而，全球化的发展虽然在世界范围内加剧了生产企业的竞争，但也在一定层面上促进了生产链条上各个企业间的分工和协作，从而导致一种新的经济组织形式出现—企业战略联盟[1]。在联盟中，企业从各自的发展战略目标和战略意图出发，为了实现共同愿景、获得最佳利益和综合优势，结合彼此的资源或优势而建立起一种优势互补、风险共担、利益共享和共同发展的正式但非合并的合作关系。在实际企业的生产过程中，战略联盟可以加深彼此间交流合作，增强信任感这一保障机制，有利于降低交易成本，激发新思想，创造新技术，促进学科交叉和产业融合，不断推动科学技术的进步等优势。

在战略联盟中，联盟是如何形成的是联盟一切活动的基础。形成战略联盟的决策行为一般受偏好、公平、信任等诸多情感因素的影响，且各联盟可以根据历史的先验信息不断调整并形成相应的合作。对联盟形成的一个重要研究方向是结合社会学、心理学及具体生产实践，谈判行为等探讨有效的联盟形成机制。近年来，国内外众多研究者针对此方面进行了大量的研究并取得了一定的研究成果。例如：龚勇[2]给出了联盟形成的行为规范机制，构建了联盟形成模型，陈莉[3]提出基于情感组织Agent的联盟形成策略，引入组织Agent的情感因子对形成联盟过程中的能力贡献进行评估，李剑[4]提出了一种联盟形成时的奖励策略，对于在联盟中执行任务的Agent给予适当奖励，从而使得联盟在达到全局最优化解的同时保持稳定，夏娜[5]给出了一种基于利益均衡的联盟形成策略，在非减性效用分配等原则的基础上，提高了对额外效用分配的合理性。目前国内外对联盟形成的决策行为的另一方面研究较多的是集中于局中人交互作用的探讨上，也取得了一定的研究成果。 比如：Owen[6]第一次提出合作对策的超可加性以来，引起了人们对经典合作对策中局中人间相互影响的研究，文献[7～9]利用给定的模糊测度探讨了局中人间的相互影响。Owen给出了两个局中人间相互影响的度量指标，Roubens[10]将其推广到两个联盟间相互影响的度量指标。上述方法均是将Shapley值和Banzhaf-Coleman指标作为局中人对合作对策贡献的期望值推广为局中人间相互影响的度量指标，由于这种均值度量指标不能反映出局中人间的相互独立性，李书金和张强[11]将经典合作对策中局中人间相互影响的研究推广到了模糊合作对策中，提出了局中人参与水平相互影响和绝对相互影响的概念。

从以上文献分析中我们可以看出关于联盟形成的研究一部分着眼于主体之间的信任与情感因素方面，一方面着重于主体间的交互作用关系方面，但由于市场环境的复杂性等因素使得联盟的形成极其复杂，我们所得的信息具有不完备性，各主体之间的关系也难以精确表达和量化，给我们对联盟形成的研究带来很大困难。因此，在不确定环境下如何量化主体之间的关系，研究联盟形成问题具有重要意义。

基于以上分析，本文做了如下工作：1)深入分析影响企业战略联盟稳定的各因素，利用G1排序法进行属性权重的分配，并用基于相似度的聚类分析法对属性权重进行筛选和修正，依靠专家打分，加权综合等方法建立各企业之间的模糊相似关系矩阵；2)运用粗糙集的相关知识，以联盟稳定性最大，以最大相容类模拟联盟成员中的关系，建立基于最大相容类的粗糙规划模型；3)结合具体实例，分析模型的有效性，为决策者进行联盟成员的选择提供决策参考。

1 预备知识

1.1 粗糙集的基本概念

粗糙集理论作为一种处理不确定性知识的数学工具，得到了学术和应用领域的广泛关注，下面介绍相关基本概念。

定义1.1[12]若U上的关系R(即论域U×U的一个子集称为U上的一个关系)同时满足自反性(即对任何x∈U，均有(x,x)∈R)、对称性(即当(x,y)∈R时，必有(y,x)∈R)和传递性(即当(x,y),(y,z)∈R时，必有(x,z)∈R)，则称R为U上的一个等价关系。当R仅满足自反性和对称性时，称R为U上的一个相似关系，我们称：

(1)

(2)

分别为X的R下近似集和R上近似集, 其中X⊂U，(x)R={y|(x,y)∈R且y∈U}.

1.2 最大相容类及其确定方法

定义1.2[13]设R是论域U上的相似关系，X⊂U且X≠Ø。若X满足：1)当x,y∈X时，必有(x,y)∈R； 2)不存在x∈U-X使得(x,y)∈R对任何y∈X恒成立，则称X是相似关系R的一个最大相容类，并用KR(U)表示R的最大相容类全体。

利用定义1.1和定义1.2易知，任何最大相容类必定包含在某一个相似类中，且U中任何元素必定属于某一个最大相容类，因而相似关系R的最大相容类不仅存在，而且KR(U)构成U的一个覆盖(即∪{Xi|Xi∈KR(U)}=U)。对于有限论域U={x1,x2,…,xn}以及U上的相似关系R，我们按照下面的步骤来确定KR(U)：

步骤1 根据相似关系R的关系矩阵MR，选择MR的主对角线以下的部分构成R的简化关系表。

步骤2 观察简化关系表，如果某元素xi对应的行和列上的值均为零，则xi单独构成一个最大相容类{xi}，并删除xi对应的行和列。

步骤3 从最后一列开始依次向左逐列观察简化关系表，直至找到至少含有一个非零元素的列，列出各个非零元素rij对应的集合{xi,xj}。

步骤4 继续向左观察，直至遇到至少含有一个非零元素的列，同样列出各个非零元素对应rij的集合{xi,xj}。观察列出的集合与之前列出的集合，如果发现某元素与之前列出的某集合中各个元素都有关系R，则将该元素加入到之前列出的集合中；如果存在某元素与之前列出的集合中的部分元素分别有关系R，则将这些有关系的元素组成新集合。最后删除可包含于其它集合中的集合。

步骤5 重复步骤4，直至观察完矩阵MR全部的列，最后得到的集合(包括单个元素构成的最大相容类)就是论域U上由相似关系R产生的全部最大相容类。

由定义1.1知，相似关系是作为描述元素之间相似特征的一种数学工具，然而相似关系在实际问题中常常难以得到恰当的应用，其本质原因是这些关系没有明确的内涵和外延，因而，采用模糊相似关系来描述元素之间的相似特征是一种更合理的方法，下面介绍模糊相似关系的定义：

定义1.3[14]设R是U上的模糊关系(即U×U上模糊集合)，R(x,y)表示R的隶属函数。若R满足自反性(即∀x∈U，R(x,x)=1)和对称性(即∀x,y∈U，R(x,y)=R(y,x))，则称R为U上的模糊相似关系。

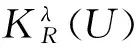
定理1.1[14]U上的模糊关系R是模糊相似关系的充分必要条件是：对任意的λ∈[0,1]，Rλ={(x,y)|R(x,y)≥λ} 为U上相似关系。

1.3 粗糙规划模型的形式化描述

粗糙规划的本质是将论域U上的某种粗糙结构特征融入决策方案的选择过程中，当U上的粗糙特征采用U上的关系来刻画时，粗糙规划的一般形式可概述为：

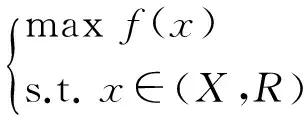
(3)

其中，X为可行域，是论域U上的某种集合，f(x)为目标函数，R为U上的某种关系，x∈(X,R)表示x与X是R相关的。

自(3)式不难看出，在决策方案的选择过程中，不仅要考虑目标f(x)的取值，而且还要兼顾与x具有R相关特征的元素的作用，因此在下文的分析中，我们将基于(3)式进行讨论。

2 影响企业战略联盟形成的属性指标权重确定方法

由于影响企业联盟稳定性的属性有很多，依据专家针对各局中人的相关属性得到的相似矩阵带有主观片面性，且各个属性对联盟稳定性的重要程度也不同，专家针对每个属性都要给出各企业之间的相似关系，如何进行相似矩阵的合并，如何让最终的矩阵具有代表性将直接影响联盟的形成。因此我们在进行矩阵综合时，主要利用加权平均的方式，充分体现各属性的重要性。此时各属性的权重的选择显得尤为重要。

在属性权重的构建过程中，我们引入序关系G1法。也即专家按照指标的序关系进行递增或递减打分，这样减少了比较次数，减少了计算量，同时也降低了专家打分的难度，提高了效率。

定义2.1[15]若评价指标Ui相对某评价准则(目标)的重要程度大于Uj， 则记为Ui≻Uj。

表1 比例标度及含义

定义2.2[15]若评价指标U1,U2,…,Um相对于某评价准则(目标)具有关系式Ui≻Uj≻…Uk, 则称评价指标U1,U2,…,Um按“≻”确定了序关系。

在指标集中依次选出指标中最重要(最不重要)的一个指标并进行排序，对评价指标集U1,U2,…,Um建立序关系，这样就可以确定一个惟一的序关系，相关指标的比例标度与含义见表1。

由于G1法确定权重主观性太强，所以在确定属性之间的权重时，我们采用基于相似度的聚类分析法来对属性权重进行筛选和修正，从而降低了权力集中和因个人偏好而引起的主观性，提高了评估结果的准确性。

本文通过计算各权重间的欧几里得贴近度来表示各位专家所得权重的相似度，并形成相似度矩阵，以此来判断各专家对属性所赋权重的离散程度。如：权重矩阵如下：

(4)

其中n表示专家个数，m表示属性个数，Wij表示第i位专家对第j个属性权重的评判。

欧几里得贴近度公式以及由欧几里得贴近度公式计算出相似度矩阵R如下：

(5)

(6)

其中，rij表示第i位专家与第j位专家对属性所赋权重值的贴近程度，rij越小，则相似程度越小，并且rij=rji,rii=1，令：

B=(b1,b2,…,bn)T

(7)

其中bi为相似系数矩阵R中第i行元素之和，它反映了专家i与专家群(含本人)意见的偏离程度。

3 基于λ-最大相容类的企业战略联盟形成决策模型

由定义2.2知，最大相容类能明确表示类中的元素之间的相互关联性，为考察企业战略联盟中各企业之间的相似关联性，首先我们需要构建各个局中人之间的模糊相似关系，继而求得λ-最大相容类，我们可按照如下步骤来构建基于λ-最大相容类的企业战略联盟形成决策模型：

步骤1 选定影响企业联盟形成稳定的相关属性C1,C2,…,Cm，专家根据经验和调查分析针对各属性对各企业进行分析，给出各企业间的模糊相似矩阵R1,R2,…Rm;

步骤2 依据第3部分中的指标权重方法，确定各属性权重α1,α2,…,αm；

步骤3 通过加权求和方法R=α1R1+α2R2+L+αmRm，确定最终的综合矩阵R；

其中：xj表示特定最大相容类中某企业，XJ表示特定最大相容类中元素组成的相似矩阵，|XJ|表示该矩阵XJ的元素个数，XI-J表示特定最大相容类中某企业与不在一个最大相容类里的其他企业组成的相似矩阵，|XI-J|表示该相似矩阵XI-J的个数，f(xij)表示第j个企业与第i个企业之间的相似度，α+β=1,α≥0,β≥0，α,β是对间接值和直接值重视程度的参数，可以根据决策者的意愿进行调整；

步骤6 求其它企业对该相容类的平均相似度(一旦该类被选取，如果其中元素不满足现实要求，则会从其他类元素中选取与该类相似度最大的元素)

其中：|XiJ|表示不在该最大相容类里的其它企业与该最大相容类中的企业组成的相似矩阵的元素个数；

步骤7 基于每一个最大相容类都会求出各企业的相似度，(如果有n个最大相容类，就会求出n组相似度)，选取其中平均相似度最大一组，进行求解；

(8)

注3.1 虽然通过阈值可以将模糊粗糙规划问题转化为一个普通的规划问题，但模型(8)却不能从整体上描述模糊粗糙规划问题的固有特征。为此，我们可以通过多种阈值下的间接效用的某种综合(比如，加权综合、积分综合等)来完善各元素的间接效用的确定机制。

步骤9 求解模型(8)，得出最终形成联盟的各个企业。

4 实例分析

北京某经济开发区在多年发展基础上，形成了具有一定规模和社会影响力的化工产业园区，园区内现有化工生产链上下游企业10家，记为{x1,x2,…,x10}，因各方面因素影响，各企业在规模上具有一定差异，所生产的产品也各具特色。当地政府为了打造特色产业，创造更大收益，增强这一化工产业园区的综合竞争能力，更好地发挥资金在公共平台建设、关键技术开发等方面的作用，计划对该园区内的化工产业投入一笔专项发展资金，决定支持由5家企业组成的、具有较大稳定性的企业联盟，但政府有一定的条件限制，即 ①：企业x1、x2中有且只能资助一个，②：企业x9、x10中有且只能资助一个，试分析政府应支持哪5家企业形成的联盟更具有合理性。

针对以上实例，依据第3部分的讨论，具有较大稳定性的战略联盟形成具体步骤如下：

(1)选定对化工企业联盟稳定性造成影响的相关属性

影响企业联盟稳定性的因素很多，各个企业之间的相似性直接影响联盟后的可持续发展，本文主要从实践经验中提取7个重要属性进行综合分析，即：C1处理与伙伴关系能力、C2未来收益重要性、C3创新能力、C4学习能力、C5伙伴的品牌知名度、C6目标差异、C7市场重叠。

请5位化工企业专家针对每一个属性对10家企业之间的相似性进行打分，形成7个模糊相似矩阵R1，R2，R3，R4，R5，R6，R7如下：

(2)依据第2部分的方法，得到7个属性的权重分配为：

表2 各属性之间的权重分配

(3)形成各企业间综合相似矩阵；

对7个相似矩阵进行加权求和，形成一个最终的相似矩阵：

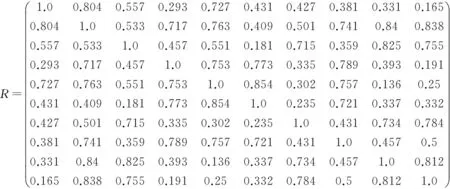
(4)选定λ，求出λ最大相容类；

表3 不同阈值下的最大相容类

(5)在最大相容类的基础上求出某相容类中企业的平均相似度，以及该类中企业与其他类中企业之间的平均相似度，最后加权求和，得出该类中各企业的相似度(本实验中，我们取α=0.2,β=0.8)。 比如：当λ取0.5时，最大相容类{x2,x8,x10}中各企业的相似度分别为0.767，0.748，0.73；

(6)当λ取0.5时，在最大相容类为{x2,x8,x10}中，其它企业对该相容类的平均相似度分别为x1=0.45，x3=0.549，x4= 0.566,x5=0.59，x6=0.487，x7=0.572,x9=0.703。当λ取0.5, 0.7, 0.8时对于不同最大相容类各企业的平均相似度如表4所示。

表4 不同阈值的各企业平均相似度

(7)从上表可以看出，当λ取0.5时，最大相容类{x2,x8,x10}所对应的一组平均相似度最大，所以选取该组数据进行求解；

(8)构建粗糙规划模型：

用以上结果来构建该问题的如下粗糙规划模型

(9)求解模型，得出符合条件的联盟为如下企业：

表5 不同阈值λ下最终形成联盟的各个企业

从理论分析和实验结果我们可以看出：1)决策结果与阈值λ直接相关，比如当λ=0.5时，企业x2,x5,x6,x8,x10会形成最为稳定的联盟，当λ=0.8时，企业x2,x3,x4,x7,x9会形成稳定的联盟，此时，阈值λ描述了企业联盟中各企业之间应满足的最低相似程度，其取值越大(小)，相应的最大相容类中的企业个数越少(多)，因而，λ是反映资助意识的一种参数，当投资力度较大(小)时，可以选择较小(大)的λ取值；2)基于最大相容类的粗糙规划模型可以求出最稳定的联盟。通过选取(排除有约束条件的)平均相似度最大的相容类进行求解，可以保证所得结果相似性高，所形成的联盟稳定性也较强。

5 结论与研究展望

本文以战略联盟形成问题为背景，深入分析影响联盟形成的各因素，以联盟稳定性最高为目标，用最大相容类刻画各联盟企业之间的相似关系，构建了相关粗糙规划模型，为联盟的有效形成提供了决策参考，但本文研究中，模型的目标只考虑了稳定性的一部分因素，如何考虑影响联盟稳定的其它因素，有效量化其余指标，将是我们下一步的研究工作。

[1] 史占中.企业战略联盟[M].上海财经大学出版社,2001.

[2] 龚勇,姚莉,张维明等.多主体系统中的联盟形成技术综述[J].计算机工程与科学,2004,26(6):100- 104.

[3] 陈莉,陈晓云,胡山立等.基于情感组织Agent的联盟形成[J].广西师范大学学报,2008,26(1):146-149.

[4] 李剑,景博,杨义先.一种基于奖励机制的Agent联盟形成策略[J].电子学报,2008,37(12A):71-75.

[5] 夏娜,蒋建国,于春华等.一种基于利益均衡的联盟形成策略[J].控制与决策,2005,20(12):1426-1428.

[6] Owen G. Multilinear extensions of games[J]. Management Sciences, 1972, 18(5): 64-79.

[7] Grabisch M. K-order additive discrete fuzzy measures and their representation[J]. Fuzzy Sets and Systems, 1997, 92(2): 167-189.

[8] Grabisch M, Roubens M. An axiomatic approach to the concept of interaction among players in cooperative games[J]. International Journal of Game Theory, 1999, 28(4): 547-565.

[9] Mikenina L, Zimmermann H. J. Improved feature selection and classification by the 2-additive fuzzy measure[J]. Fuzzy Sets and Systems, 1999, 107(2): 195-218.

[10] Roubens M. Interaction between criteria and definition of weights in MCDA problems[C]. In: 44th Meeting of the European Working Group “Multicriteria Aid for Decision”. Brussels, Belgium, 1996.

[11] 李书金,张强.模糊合作博弈局中人参与水平间相互作用度量[J].应用数学学报,2007,6(30):1117-1129.

[12] Pawlak Z, Rough sets. International journal of computer and information sciences[J]. 1982, 11(5): 341-356.

[13] 左孝凌,李为,刘永才.离散数学[M].上海:上海科学技术出版社,1981.

[14] Polkowski L, Skowron A. Fuzzy similarity relation as a basis for rough approximations[M]. Heidelberg: Springer-Verlag, 1998.

[15] 郭亚军著.综合评价理论与方法[M].北京:科学出版社,2002.

Aλ-Maximal Compatible Classes-Based Rough Programming Model and Its Application to Coalition Formation Decision Making Problems of Enterprise Strategic Alliance

GUAN Fei1, ZHANG Qiang1, LI Jun2

(1.SchoolofManagementandEconomics,BeijingInstituteofTechnology,Beijing100081,China; 2.StateGridShijiazhuangElectricPowerSupplyCompany,Shijiazhuang050000,China)

Enterprise strategic alliance is a new kind of win-win business competition mode. In recent years, its coalition formation problem has aroused more and more concern in the field of academic and application areas. In this paper, based on the analysis of the affecting factors of coalition formation, firstly, we give the weight indexes of these factors by the order relationG1 method, screen and revise these weight indexes by clustering analysis method based on similarity. Then we choose the highest alliance stability as the goal, usingλ-maximal compatible classes to simulate the relationship between each enterprise in the coalition, and we construct aλ-maximal compatible classes-based rough programming model using the properties and characteristics of rough planning model. Finally, by a specific example, the performance and characteristics of our model are verified and the results show that our model enriches the existing theory and provide reference for the correct decision making of coalition formation.

enterprise strategic alliance; coalition formation; maximal compatible classes; rough programming model

2013-11-17

国家自然科学基金和高等学校博士学科点专项科研基金资助(71071018,70801064,20111101110036)

关菲(1985-)，女，在读博士, 研究方向：模糊合作对策与决策, 数据挖掘;张强(1955-)男,教授,博士生导师,研究方向:模糊合作对策与决策。

O225;O221

A

1007-3221(2015)02- 0229- 08