不确定偏好序信息下考虑主体心理行为的双边匹配决策方法

乐 琦， 张 磊， 张莉莉

(1.江西财经大学 信息管理学院，江西 南昌 330013; 2.北京交通大学 经济管理学院，北京 100044; 3.辽宁科技大学 工商管理学院，辽宁 鞍山 114051)



不确定偏好序信息下考虑主体心理行为的双边匹配决策方法

乐 琦1， 张 磊2， 张莉莉3

(1.江西财经大学 信息管理学院，江西 南昌 330013; 2.北京交通大学 经济管理学院，北京 100044; 3.辽宁科技大学 工商管理学院，辽宁 鞍山 114051)

针对基于不确定偏好序信息的双边匹配问题，本文提出了一种决策方法。给出了双边匹配和不确定偏好序的相关概念，同时给出了不确定偏好序信息下考虑主体心理行为的双边匹配问题描述；以每个主体给出的临界值作为其参照点，计算了每个主体给出的不确定偏好序相对于参照点的收益或损失；考虑到主体损失规避的心理行为特征，依据TODIM思想计算每个主体对另一方主体的益损值的感知价值；在此基础上，构建了求解该双边匹配问题的双目标优化模型，使用线性加权法将双目标优化模型转化为单目标优化模型，通过求解该单目标优化模型获得匹配结果；最后，通过IT服务外包中的供给方与需求方的双边匹配实例分析说明了所提方法的有效性。

管理科学；双边匹配；不确定偏好序；心理行为；TODIM；感知价值；优化模型

0 引言

现实生活中存在着大量的双边匹配问题，如婚姻匹配问题[1]、商品买卖问题[2]、员工/求职者与岗位匹配问题[3]、大学招生录取问题[4]等。随着社会经济的发展，经济管理中的双边匹配问题引起了更为广泛关注，如二手房交易匹配问题[5]、风险投资商与风险企业匹配问题[6]。因此，双边匹配问题具有广泛的实际应用背景。

针对基于偏好序信息的双边匹配问题的研究，多年来一直受到了学者们的广泛关注。Roth针对美国医学院毕业生与实习医院的匹配问题，提出了Hospital-Resident算法[7]。Irving等针对医学院毕业生与实习医院的匹配问题，着重分析了强稳定性的概念[8]。Ehlers指出对于英国初级医药市场和部分美国公立学校录取的优先权机制与线性规划机制，在一个对称或不完全信息环境下，通过提交部分真实偏好才可能获益[9]。Alkan研究了每个主体可能与多个合作者匹配情形下的双边市场中稳定匹配的结构，即稳定多合作者匹配的格结构，指出格具有两极性、分配性、互补性以及完全配额性[10]。Sethuraman等聚焦于多对一稳定匹配问题的可行解的几何结构和公平性——非基解稳定匹配的研究[11]。Knoblauch研究了具有随机分布偏好序偏好的Gale-Shapley算法的性质[12]。

已有的研究为解决基于偏好序信息的双边匹配问题提供了理论与方法层面的借鉴指导，也扩大了实际应用背景。但需要指出的是，一方面在一些现实匹配问题中，双方主体给出的偏好信息可能是不确定偏好序，但关于不确定偏好序信息下的双边匹配决策问题的研究非常少见；另一方面已有研究大多从稳定性和满意性角度进行研究，在这些研究中主体往往被认为是完全理性的，没有考虑到主体的心理行为因素；而现实决策过程中，大多数主体是有限理性的[13]。为此，本文针对不确定偏好序信息下的双边匹配问题，提出了一种考虑主体心理行为的双边匹配决策方法。

1 相关基础知识

1.1 双边匹配

双边匹配的相关概念及其符号描述可参照文献[14～16]。进一步可知，双边匹配μ可表示为μ=μM∪μS，其中μM为匹配主体对集合，μS为单身主体对集合。

1.2 不确定偏好序

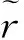
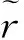
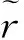
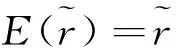
(1)

2 问题描述

根据上述分析，不确定偏好序信息下考虑主体心理行为的双边匹配问题，可由图1表示。图1中，Ai与Bj之间的有向虚线的权值表示它们之间的偏好序大小，Ai与Bj之间的无向粗线表示Ai与Bj匹配；由m条无向粗线连接形成的匹配主体对集合表示μE，Bn-1在该匹配μ中为单身。

3 双边匹配决策方法

为了解决上述问题，下面阐述本文提出的考虑主体心理行为的双边匹配决策方法。

3.1 感知价值矩阵的构建

首先，由于主体的临界值能很好地反映该主体的心理感受，即若Ai与排在其临界值fi之前的Bj′匹配，即rij′fk，则Ak的心理感受为损失，且tkj″越大，损失也越大；且临界值作为参照点能够很好地继承前景理论的各种性质[18]，因此，本文以临界值作为参照点。

(2)

(3)

(4)

(5)

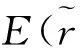
(6)

(7)

根据前景理论可知，在双边匹配问题中，主体面对收益时是风险规避的，面对损失时是风险寻求的，且对损失比收益更敏感。考虑到主体对收益和损失的不同风险态度，下面依据TODIM[19]思想，计算每个主体对另一方每个主体的益损值的感知价值。

(8)

其中θi为衰减系数，0<θi<1，θi<1表示主体面对损失比收益更敏感，θi越小表明主体Ai的损失规避程度越高。

(9)

其中ωj是衰减系数，0<ωj<1，ωj<1表示主体面对损失比收益更敏感，ωj越小表明主体Bj的损失规避程度越高。

3.2 决策模型的构建

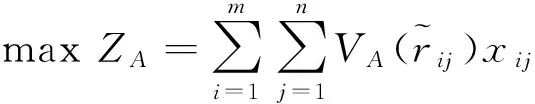
(10a)

(10b)

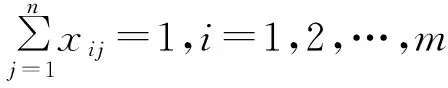
(10c)

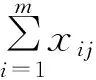
(10d)

xij=0或1,i=1,2,…,m;j=1,2,…,n

(10e)

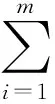
3.3 决策模型的求解

(11a) s.t. (10c)～(10e)

其中cij=wAVA(rij)+wBVB(tij)，权重wD(D=A,B)反映了目标ZD在实际双边匹配问题中的重要程度，它由中介与甲乙双方主体磋商后给出，若考虑到甲乙双方主体的公平性，则有wA=wB。

显然，模型(11)可转化为标准的指派问题模型，这样可使用匈牙利法进行求解。当模型(11)中的变量和约束条件个数较多时，可采用Lingo 11.0、Cplex 9.0、WinQSB 2.0等软件，或采用启发式方法，如遗传算法、禁忌搜索算法等进行求解。根据模型求解结果，可获得双边匹配方案。

定理10 模型(11)存在最优解，且目标函数最优值F*>0。

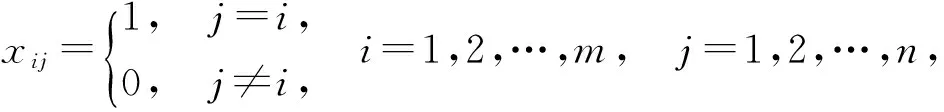
根据多目标规划理论可知，模型(11)的最优解是模型(10)的有效解。

综上，求解基于不确定偏好序信息的双边匹配问题的步骤如下：

步骤5 运用线性加权法，将双目标优化模型(10)转化为单目标优化模型(11)；

步骤6 求解优化模型(11)，获得匹配结果μ。

4 实例分析

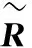
表1 不确定偏好序向量i和临界值fi

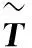
表2 不确定偏好序向量j和临界值hj

为了解决该双边匹配问题，下面简要说明使用上文给出方法的计算过程。

表3 益损矩阵F=[F(rij%)]5×6

表4 益损矩阵

表5 感知价值矩阵VA=[VA(rij%)]5×6

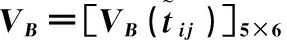
表6 感知价值矩阵

表7 系数矩阵[cij]5×6

为进一步阐明本文提出方法的意义，给出如下分析。

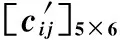
表8 系数矩阵

表9所示了考虑主体心理行为与不考虑主体心理行为的双边匹配决策方法的匹配结果。从表9中可知：运用这两种双边匹配决策方法获得的匹配结果完全不同。这就说明了主体心理行为对匹配结果有着重要的影响作用。

表9 两种决策方法的双边匹配结果μ*

5 结语

本文从主体心理行为的角度出发，将临界值视为参照点，通过定义不确定偏好序的期望与其参照点之间的规范化距离，计算了相对于参照点的收益或损失，进而依据TODIM思想计算了每个主体针对另一方主体的益损值的感知价值，在此基础上，提出了不确定偏好序信息下考虑主体心理行为的双边匹配决策方法，主要结论如下。

(1)本文将主体心理行为因素引入到双边匹配问题的研究中，丰富并发展了双边匹配的相关理论，为后续开展双边匹配理论与方法的相关研究提供了新思路。

(2)本文提出的感知价值公式能够有效的测度双方主体的心理行为。

(3)主体心理行为对匹配结果有着重要的影响作用。

(4)考虑到现实大多数主体是有限理性的，因此，本文提出的方法更能反映主体实际决策行为。

此外，本文提出的新方法具有概念清晰、实用有效的特点，对双边匹配相关理论、方法与应用等方面研究也具有较强的指导价值。

[1] Eeckhout J. On the uniqueness of stable marriage matchings[J]. Economics Letters, 2000, 69(1): 1-11.

[2] Jung J J, Jo G S. Brokerage between buyer and seller agents using constraint satisfaction problem models[J]. Decision Support Systems, 2000, 211(4): 293-304.

[3] Goodman S A, Svyantek D J. Person-organization fit and contextual performance: do shared value matter[J]. Journal of Vocational Behavior, 1999, 55(2): 254-275.

[4] Pais J. Random matching in the college admissions problem[J]. Economic Theory, 2008, 35(1), 99-116.

[5] 陈林,朱卫平.基于二手市场与理性预期的房地产市场机制研究[J].管理科学学报,2011,14(2):61-100.

[7] Roth A E. On the allocation of residents to rural hospitals: a general property of two-sides matching markets[J]. Econometrica, 1986, 54(2): 425- 427.

[8] Irving R W, Manlove D F, Scott S. Strong stability in the hospitals/residents problem[J]. Lecture Notes in Computer Science, 2003, 2607(1): 439- 450.

[9] Ehlers L. Truncation strategies in matching markets[J]. Mathematics of Operations Research, 2008, 33(2): 327-335.

[10] Alkan A. On preferences over subsets and the lattice structure of stable matchings[J]. Review of Economic Design, 2001, 6(1): 99-111.

[11] Sethuraman J, Teo C P, Qian L. Many-to-one stable matching: geometry and fairness[J]. Mathematics of Operations Research, 2006, 31(3): 581-596.

[12] Knoblauch V. Marriage matching and gender satisfaction[J]. Social Choice and Welfare, 2009, 32(1): 15-27.

[13] Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-291.

[14] 乐琦,樊治平.基于累积前景理论的双边匹配决策方法[J].系统工程学报,2013,28(1):38- 46.

[15] 乐琦,樊治平.一种具有序值信息的双边匹配决策方法[J].系统工程学报,2012,27(2):150-159.

[16] 乐琦,樊治平.具有不确定偏好序信息的双边匹配决策问题研究[J].运筹与管理,2012,21(1):57- 63.

[17] Fan Z P, Yue Q, Feng B, et al. An approach to group decision-making with uncertain preference ordinals[J]. Computers & Industrial Engineering, 2010, 58(1): 51-57.

[18] Chip H, Richard P L, Wu G. Goals as reference points[J]. Cognitive Psychology, 1999, 38(1): 79-109.

[19] Gomes L F A M, Lima M M P P. TODIM: Basics and application to multicriteria ranking of projects with environmental impacts[J]. Foundations of Computing and Decision Sciences, 1992, 16(4): 113-127.

[20] Tversky A, Kahneman D. Loss aversion in riskless choice: a reference-dependent model[J]. Quarterly Journal of Economics, 1991, 106(4): 1039-1061.

Decision Method for Two-sided Matching Considering Agents’ Psychological Behavior with Uncertain Preference Ordinal Information

YUE Qi1, ZHANG Lei2, ZHANG Li-li3

(1.SchoolofInformationManagement,JiangxiUniversityofFinanceandEconomics,Nanchang330013,China; 2.SchoolofEconomics&Management,BeijingJiaotongUinversity,Beijing100044,China; 3.SchoolofBusinessAdministration,LiaoningScienceandTechnologyUniversity,Anshan114051,China)

With regard to the two-sided matching problem based on uncertain preference ordinal information, a decision method is proposed. The related concepts of two-sided matching and uncertain preference ordinal are firstly introduced, and the problem description of two-sided matching considering agents’ psychological behavior with uncertain preference ordinal information is given. Secondly, the threshold value given by each agent is chosen as the reference point, and the gain and loss relative to the reference point corresponding to the uncertain preference ordinal given by each agent are calculated. Considering trait of loss aversion of the agent’s psychological behavior, the perceived value of gain and loss of each agent with respect to the agent of the other side is calculated according to the idea of TODIM. Furthermore, a bi-objective optimization model is developed. By using linear weighted method, the bi-objective optimization model is converted into a single objective model. The matching result is obtained by solving the model. Finally, an illustrative example of two-sided matching between demanders and suppliers in IT service outsourcing is used to illustrate the validity of the proposed method.

management science; two-sided matching; uncertain preference ordinal; psychological behavior; TODIM; perceived value; optimization model

2013- 05- 20

国家自然科学基金资助项目(71261007,71261006,71361021)

乐琦(1983-)，男，江西东乡人，江西财经大学信息管理学院讲师，博士，研究方向：管理决策分析与运筹学。

C931

A

1007-3221(2015)02- 0113- 08