考虑群体参照点的多属性决策方法

张 晓， 樊治平

(1.西安电子科技大学 经济与管理学院, 陕西 西安 710071； 2.东北大学 工商管理学院, 辽宁 沈阳 110819)



考虑群体参照点的多属性决策方法

张 晓1， 樊治平2

(1.西安电子科技大学 经济与管理学院, 陕西 西安 710071； 2.东北大学 工商管理学院, 辽宁 沈阳 110819)

针对考虑群体参照点的多属性决策问题，提出一种基于前景理论的决策分析方法。在提出的方法中，考虑了群体成员的心理行为。首先，依据D-S证据理论的思想，计算各参与决策人的参照点对群体参照点的影响度，进而确定群体参照点；然后，依据前景理论分别建立相对于群体参照点的群体收益矩阵和群体损失矩阵，并通过计算每个方案的群体前景值进行方案排序。最后，实例分析说明了提出方法的可行性。

管理科学；多属性决策；前景理论；群体参照点；群体前景值

0 引言

多属性决策是与多个属性有关的有限方案选择问题[1]，其在经济管理领域中有着广泛的实际背景。在现实的多属性决策问题中，决策者可能会依据历史信息、当前状态或者对未来预期等对各属性有心理参照点[2,3]，例如，在选择一台制造设备[3]时，决策者对设备的载重能力的参照点为2吨，对设备每小时固定运行成本的参照点为2美元。因此，如何解决考虑决策者给出参照点的多属性决策问题，是一个值得关注的研究课题。

目前，关于考虑决策者给出参照点的多属性决策方法研究已经引起了一些学者的关注，从已有研究成果来看，主要有两类决策分析方法。一类是基于交互式程序的决策方法[4～7]，这类决策方法考虑决策者的行为是完全理性的，首先给出寻找最接近参照点的非占优方案的算法，然后运用不同的交互式模型通过调整决策者对属性的参照点来得到最优方案。另一类是基于前景理论[2,8]的决策方法[3,9～14]，这类决策方法考虑决策者的行为是有限理性的，即考虑到在决策过程中，决策者会将方案的属性值与参照点进行比较，将超过参照点的部分视为“收益”，没有达到参照点的部分视为“损失”，并且对待“收益”和“损失”有不同的心理反映。这类决策方法的基本原理是首先计算属性值相对于参照点的收益或损失，然后依据前景理论计算方案的前景值，并依据前景值的大小进行方案排序。上述两类方法为解决考虑决策者给出参照点的多属性决策问题提供了较好的决策模型与方法的支撑，特别是第二类决策方法可使得到的决策结果能够反映决策者的心理行为。但需要指出的是，在一些现实的多属性决策问题中，往往会有多人参与决策，并且每个参与决策人可能会针对各属性给出不同的参照点，这就是考虑多人给出参考点或群体参照点的多属性决策问题。例如，对于产品设计方案选择问题，通常由设计小组中的多名设计人员共同参与决策，每个设计人员针对产品设计方案的制造成本、重量等诸多属性给出的参照点往往不同或存在差异。因此，在考虑群体成员心理行为的情况下，如何给出一种有针对性的解决考虑群体参照点的多属性决策问题的决策分析方法是十分必要的。其中，解决问题的关键是如何依据多人给出的参照点来确定群体参照点。

基于以上分析，本文则是给出一种基于前景理论的决策方法。该方法是依据多人给出的参照点，计算个体参照点对群体参照点的影响度来确定群体参照点，即给出一种基于D-S理论的群体参照点确定方法；进一步地，依据前景理论，将决策矩阵转化为相对于群体参照点的群体收益矩阵和群体损失矩阵，并在此基础上通过计算各方案的群体前景值对所有方案进行排序。

1 问题描述

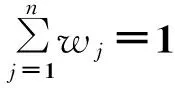
本文要解决的问题是：在考虑多个参与决策人心理行为的情况下，依据决策矩阵X、属性权重向量w和群体参照点矩阵R，如何通过一个有效的决策分析方法得到所有方案的排序结果。

2 决策方法

为了解决上述问题，下面阐述本文提出的基于前景理论的决策分析方法。提出方法涉及两个关键部分：群体参照点的确定和群体前景值的计算，下面分别给出这两个部分计算过程的描述。

2.1 群体参照点的确定

(1)

群体参照点Rj没有被分配的基本概率函数为

(2)

(3)

(4)

(5)

依据式(1)～(5)对kj个证据下的判断信息进行合成之后，可得到群体参照点Rj关于识别框Θj的综合可信度，即

(6)

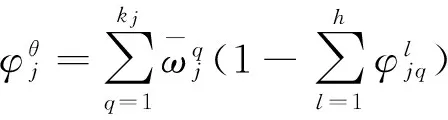
(7)

(8)

(9)

在此基础上，可计算得到针对属性Cj的群体参照点Rj，其计算公式为

(10)

2.2 群体前景值的计算

针对决策矩阵X=[xij]m×n和各属性的群体参照点R1,R2,…,Rn，计算每个方案针对各属性的属性值相对于群体参照点的收益和损失。属性值xij相对于群体参照点Rj的收益Gij的计算公式为

(11)

(12)

损失Lij的计算公式为

(13)

(14)

依据式(11)～(14)，可分别建立群体收益矩阵G=[Gij]m×n和群体损失矩阵L=[Lij]m×n。显然，Gij≥0，Lij≤0，i∈M，j∈N。

针对矩阵G=[Gij]m×n和L=[Lij]m×n，考虑到决策者对待收益和损失的不同心理反映，分别计算每个方案针对各属性的群体前景值。依据前景理论[8]，群体前景值Vij的计算公式为

Vij=(Gij)α-λ(-Lij)β,i∈M,j∈N

(15)

其中，α和β分别表示价值函数的收益区域和损失区域的凹凸程度，其反映了决策者对待收益和损失的不同风险态度[8]，0<α<1，0<β<1；λ表示决策者的损失规避程度[8]，λ>1，λ越大，表明决策者的损失规避程度越大。

这里需要说明的是，在文献[8]中，Kahneman和Tversky运用参数法对大量实验结果进行拟合，得到参数α、β和λ的取值分别为α=β=0.88，λ=2.25，它们能够表示任意决策者大致的行为偏好，因此，在式(15)中取α=β=0.88，λ=2.25。依据式(15)，可建立群体前景决策矩阵V=[Vij]m×n。

(16)

其中

(17)

依据简单加权方法，计算每个方案的群体综合前景值Ui，其计算公式为

(18)

显然，Ui越大，方案Ai越好。因此，依据Ui值的大小，可对方案进行排序。

综上所述，考虑群体参照点的多属性决策方法的计算步骤如下：

步骤1 依据式(1)～(10)计算针对每个属性的群体参照点Rj。

步骤2 依据式(11)～(14)分别建立群体收益矩阵G=[Gij]m×n和群体损失矩阵L=[Lij]m×n。

步骤3 依据式(15)建立群体前景决策矩阵V=[Vij]m×n。

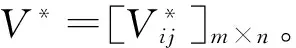
步骤5 依据式(18)计算每个方案的群体综合前景值Ui，并依据Ui值的大小对方案进行排序。

3 实例分析

AT电子产品公司考虑开发一种个人掌上电脑并投放市场，现有5个备选设计方案(A1,A2,…,A5)，考虑的属性有3个(C1,C2,C3)，其中，C1为制造成本(单位：元)，C2为电池连续使用时间(单位：小时)，C3为产品重量(单位：克)。在这3个属性中，C1属性和C3为成本型属性，C2属性为效益型属性。假设该公司决策活动组织者提供的属性权重向量为ω=(0.50,0.30,0.20)，决策矩阵如表1所示。该公司的产品设计小组中的5个专家给出的参照点矩阵如表2所示。为了解决该决策问题，下面简要说明采用本文给出的方法的计算过程。

表1 备选设计方案的决策矩阵

表2 产品设计小组成员的参照点矩阵

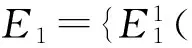
然后，依据式(1)～(7)，将针对每个证据的群体参照点Rj的判断信息进行合成，可以得到规模化因子和基本概率分配函数如下：

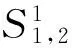
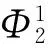
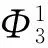
在此基础上，可得到针对各属性的概率分布形式的群体参照点如表4所示，并依据式(8)～(10)计算得到针对各属性的群体参照点分别为：R1=1079，R2=18，R3=124。

表4 概率分布形式的群体参照点

依据式(11)～(14)分别建立群体收益矩阵G=[Gij]m×n和群体损失矩阵L=[Lij]m×n，即

进一步地，依据式(15)建立群体前景决策矩阵，并依据式(16)和(17)建立规范化群体前景决策矩阵，即

依据式(18)计算得到每个方案的群体综合前景值为：U1=-0.43，U2=-0.40，U3=-0.66，U4=-0.14，U5=-0.17。依据前景值的大小，可以得到方案的排序结果为：A4≻A5≻A2≻A1≻A3，即选择设计方案A4投放市场。

4 结束语

本文针对考虑群体参照点的多属性决策问题，给出了一种基于前景理论的决策分析方法。该方法考虑了群体成员的心理行为，首先通过计算各参与决策人的参照点对群体参照点的影响度来确定群体参照点，然后依据前景理论的思想将决策矩阵转化为相对于群体参照点的群体收益矩阵和群体损失矩阵，在基础上，通过计算方案的群体前景值进行方案排序。本文提出的方法，能够使得到的决策结果反映群体成员的行为，并且具有概念清晰、计算简单等特点，有较强的可操作性和实用性，为解决考虑群体参照点的多属性决策问题提供了一种新途径。

[1] Tzeng G H, Huang J J. Multiple attribute decision making: methods and applications[M]. New York: CRC Press, 2011.

[2] Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-291.

[3] Fan Z P, Zhang X, Chen F D, Liu Y. Multiple attribute decision making considering aspiration-levels: a method based on prospect theory[J]. Computers & Industrial Engineering, 2013, 65(2): 341-350.

[4] Lotfi V, Stewart T J. An aspiration-level interactive model for multiple criteria decision making[J]. Computers & Operation Research, 1992, 19(7): 671- 687.

[5] Nowak M. INSDECM-an interactive procedure for stochastic multicriteria decision problems[J]. European Journal of Operational Research, 2006, 175(3): 1413-1430.

[6] Nowak M. Aspiration level approach in stochastic MCDM problems[J]. European Journal of Operational Research, 2007, 177(3): 1626-1640.

[7] Wang J G, Zionts S. The aspiration level interactive method(AIM)reconsidered: robustness of solutions[J]. European Journal of Operational Research, 2006, 175(2): 948-958.

[8] Tversky A, Kahneman D. Advances in prospect theory: cumulative representation of uncertainty[J]. Journal of Risk and Uncertainty, 1992, 5(4): 297-323.

[9] 王坚强,周玲.基于前景理论的灰色随机多准则决策方法[J].系统工程理论与实践,2010,30(9):1658-1664.

[10] Liu P D, Jin F, Zhang X, Su Y, et al. Research on the multi-attribute decision-making under risk with interval probability based on prospect theory and the uncertain linguistic variables[J]. Knowledge-Based Systems, 2011, 24(4): 554-561.

[11] 张晓,樊治平.一种基于前景理论的风险型区间多属性决策方法[J].运筹与管理,2012,21(3):44-50.

[12] 李鹏,刘思峰,朱建军.基于前景理论的随机直觉模糊决策方法[J].控制与决策,2012,27(11):1601-1606.

[13] 张晓,樊治平.基于前景理论的风险型混合多属性决策方法[J].系统工程学报,2012,27(6):772-781.

[14] 刘成明.多属性行为决策方法研究[D].长春:吉林大学,2009.

[15] Shafer G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976.

[16] Yang J B. Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties[J]. European Journal of Operational Research, 2006, 131(1): 31- 61.

[17] Fu C, Yang S L. An evidential reasoning based consensus model for multiple attribute group decision analysis problems with interval-valued group consensus requirements[J]. European Journal of Operational Research, 2012, 223(1): 167-176.

Method for Multiple Attribute Decision Making with Group Reference Points

ZHANG Xiao1, FAN Zhi-ping2

(1.School of Economics and Management, Xi Dian University, Xi’an 710071, China; 2.School of Business Administration, Northeastern University, Shenyang 110819, China)

A decision analysis method based on prospect theory is proposed to solve the multiple attribute decision making problem with group reference points. First, according to the idea of D-S theory, the group reference point for each attribute is determined by calculating the influence degree of each member’s reference point to the group reference point. Then, based on prospect theory, the group gain matrix and group loss matrix of the decision matrix relative to group reference points are constructed, respectively. Further, the ranking of alternatives can be determined by calculating group prospect values for alternatives. Finally, a practical example is given to illustrate the feasibility of the proposed method.

management science; multiple attribute decision making; prospect theory; group reference point; group prospect value

2013- 08-28

国家自然科学基金资助项目(71401131)；高等学校博士学科点专项科研基金新教师类资助课题(20130203120024)；陕西省自然科学基础研究计划资助项目(2013JQ9002)；中央高校基本科研业务费专项资金资助项目(BDY251412,JB150601)；教育部中国移动科研基金(MCM20122031)

张晓(1985-)，女，河南南阳人，博士，讲师，研究方向：决策理论与方法。

C 934

A

1007-3221(2015)03- 0106- 06