竖直圆管内超临界压力氟利昂传热试验研究

张思宇，程 旭，顾汉洋

（1.上海交通大学核科学与工程学院，上海 200240；2.环境保护部核与辐射安全中心，北京 100082）

竖直圆管内超临界压力氟利昂传热试验研究

张思宇1，2，程 旭1，顾汉洋1

（1.上海交通大学核科学与工程学院，上海 200240；2.环境保护部核与辐射安全中心，北京 100082）

深入研究超临界压力下流体特殊的对流传热特性，对超临界水冷反应堆的堆芯设计至关重要。在上海交通大学SMOTH氟利昂回路上开展了压力4.3～4.7 MPa、质量流速600～2 500 kg／（m2·s）、热流密度20～180 kW／m2参数下的圆管内超临界上升流传热试验。远离拟临界温度区间内换热系数和Dittus－Boelter公式计算值很接近，热流密度越大，近拟临界区换热系数越小，小质量流速大热流密度下，发生显著传热恶化。加速效应无量纲数和浮升力无量纲数对传热特性显示了强烈的相关性。提出了氟利昂工质传热试验的传热恶化起始点关系式。Bishop关系式计算换热系数和试验值之间标准差很小，但整体略偏大；Jackson关系式计算值和试验值之间平均偏差很小，但标准差偏大。

超临界传热；换热系数；传热关系式；无量纲数；传热恶化

超临界水冷堆正常运行的压力、温度高于水的临界点（22.1 MPa，374℃），相对于现有传统水冷反应堆，具有更高的热效率和简化的系统，同时具有良好的技术继承性［1］。在超临界压力下，尤其在拟临界温度附近，流体的各项热物性发生剧烈变化，从而表现出显著不同的传热特性，热流密度对换热系数影响很大，在不同工况条件下可能发生传热强化和传热恶化现象［2］。针对超临界流体的热工水力研究对于超临界水冷堆的堆芯设计和安全运行至关重要。

在以超临界火电站和超临界新型制冷剂为背景的研究下，已开展了大量圆管内超临界流体的流动传热试验［3－4］，总结了热流密度和质量流速等参数对传热的影响，发现了由浮升效应引起的传热恶化现象。通过相关无量纲数的整理，对传统亚临界压力下对流传热关联式进行修正，文献中提出了多种传热经验关联式［5－7］。但由于对传热机理的认识有限，目前还没有公认的传热关系式能够以满意的精度适用于广泛参数范围内得到的试验数据。

在超临界水冷反应堆被选定为6种第四代新型核反应堆中的唯一水冷堆型的背景下，上海交通大学建立了超临界氟利昂模化流体试验回路，进行了系统的超临界传热试验，得到了正常传热和传热恶化现象的数据。本文对传热的影响因素进行分析，量化浮升效应和加速效应无量纲数对传热特性的影响，对现有代表性超临界压力下对流换热经验关联式进行验证评价。推进认识超临界流体传热机理、建立更准确且广泛适用的计算关系式和超临界流体间模化准则的工作。

1 试验系统和方法

1.1 试验回路与试验本体

上海交通大学SMOTH试验回路流程图如图1所示。试验回路包括主试验回路系统、循环冷却水系统和氟利昂充液回收系统。试验工质为氟利昂R134a，试验系统最高运行压力6 MPa，流体最高温度120℃，最大试验流量10 m3／h。氟利昂经主循环泵出口流出后，根据试验需要，分别进入大小两条试验支路，由预热器加热到所需温度后，进入试验本体内流道，流体流出试验本体出口，在混合器中与未经加热的冷流体混合后，再经过换热器的进一步冷却，流回主循环泵。系统的压力由连接至主循环泵入口的稳压器稳定和调节。试验本体以硅整流系统提供的直流电直接加热，预热器则由调压器控制交流电进行加热。

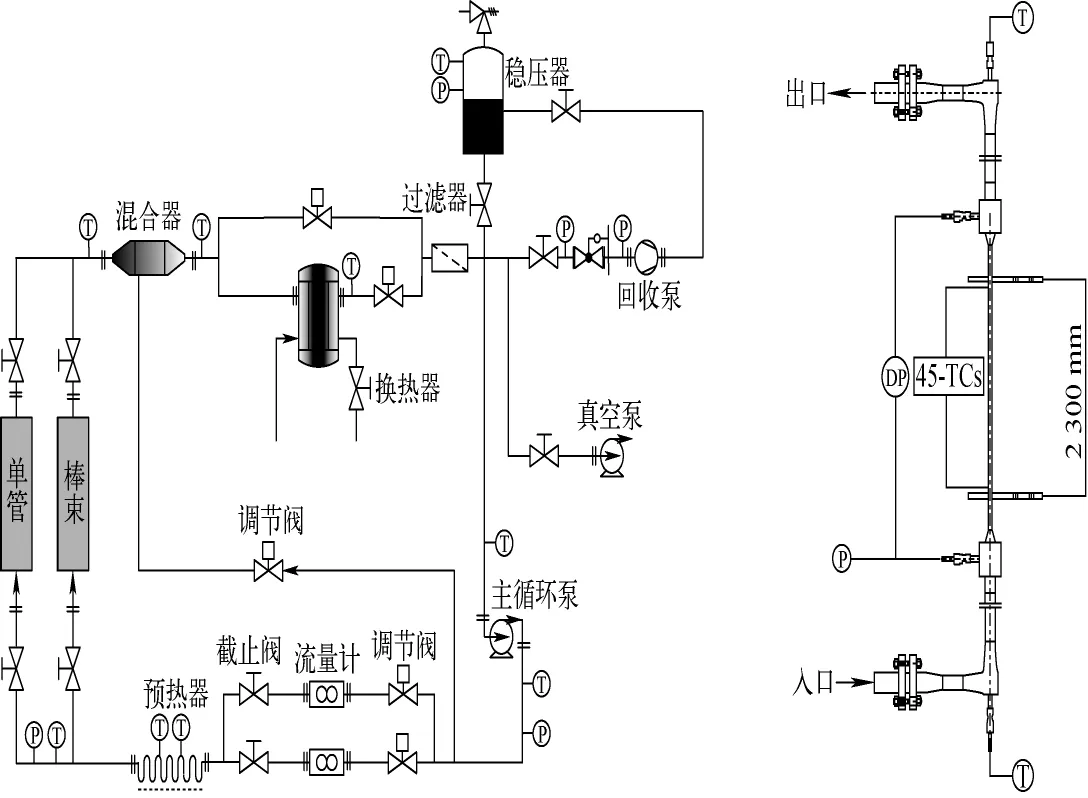
图1 SMOTH回路流程图和试验段设计图Fig.1 Schematic diagram of SMOTH test facility and test section

圆管试验段采用因科镍625制造，内径7.6 mm，外径12.0 mm，加热长度2.3 m。试验段入口压力由0.2级精度的压力变送器测量，流量由0.1级精度的质量流量计测量，进出口流体温度及壁面温度均由1级精度的铠装T型热电偶测量，壁温测量热电偶间隔50 mm均布在2.3 m长的加热壁面上，加热段上下游各有约0.5 mm的绝热发展段。

1.2 数据处理方法

测量得到加热直流电的电压、电流及热效率，可得到圆管试验段内壁面热流密度q（W／m2）：

式中：U为试验段电压，V；I为试验段电流，A；Di为圆管试验段内径，m；L为试验段加热长度，m；η为电加热效率。

根据能量守恒，由入口温度、流量、热流密度计算得到流体主流温度轴向分布：

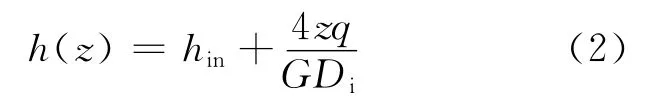
式中：h（z）为z高度位置对应的流体比焓，J／kg；hin为试验段入口处流体比焓，J／kg；z为沿轴向高度，m；G为流体质量流速，kg／（m2·s）。

圆管试验段周向对称，轴向导热很小，可忽略，以一维导热问题处理。试验段材料因科镍625的电阻率随温度变化很小，可近似以均匀内热源处理。试验段外壁面温度由T型热电偶测得，通过离散化一维均匀内热源导热计算，得到内壁面温度：

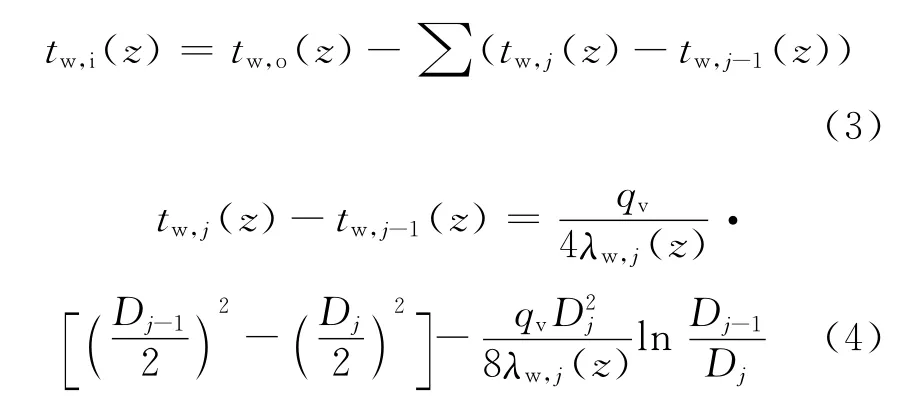
式中：tw，i（z）为z高度位置对应试验段内壁面温度，℃；tw，o（z）为z高度位置对应试验段外壁面温度，℃；tw，j（z）为z高度位置对应试验段内第j层节点壁面温度，℃；qv为试验段平均体积释热率，W／m3；λw，j（z）为试验段z高度位置第j层节点导热系数，W／（m·K）；Dj为第j层节点试验段直径，m。

z高度位置的当地流体对流换热系数α（z）（W／（m2·K））为：

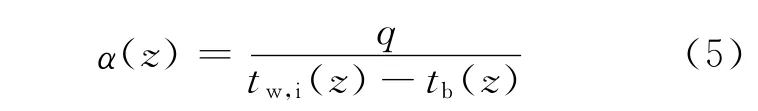
式中：tw，i（z）为对应的试验段内壁面温度，℃；tb（z）为对应的流体主流温度，℃。

1.3 不确定度分析

试验研究中直接测量的参数包括压力、流量、流体温度、壁面温度、电流、电压、试验段管径和壁厚等，测量参数的不确定度列于表1。

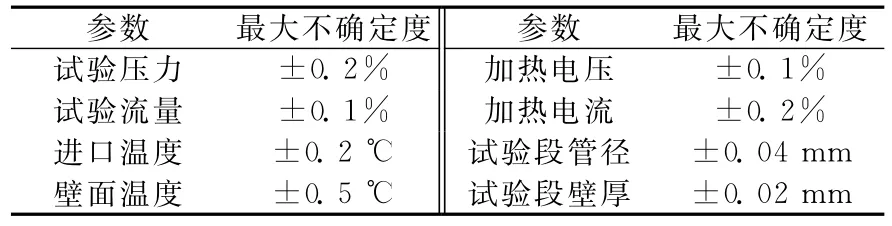
表1 测量参数的不确定度Table 1 Uncertainties of parameters

根据2σ（置信度95%）准则，在4 080个试验数据点中，以Nu的不确定度衡量，88.3%的数据点不确定度在5%以内，99.8%的数据点不确定度在10%以内。

2 试验结果和分析

2.1 热流密度的影响

在压力4.3 MPa、质量流速1 000 kg／（m2·s）的一组典型工况中，不同热流密度下超临界氟利昂的传热特性如图2所示。其中，tb为流体温度，tw为内壁面温度，hb为流体比焓，α为对流换热系数，hpc为拟临界温度tpc对应的流体比焓。由图2可见，壁面温度随流体比焓增加而上升，在达到拟临界比焓前的一段区域内壁温上升很平缓，相应的对流换热系数达到峰值。小热流密度下，换热系数持续增大至接近拟临界比焓时达到最大值，壁温始终随流体比焓增加而缓慢上升；较大热流密度下，在远离拟临界点的低焓区，换热系数和小热流密度下几乎完全相同，但随着流体比焓升高，近壁面缓冲区流体接近拟临界温度，密度剧烈减小，产生的浮升力显著地削弱了切应力和湍流强度，使换热系数不再增大，甚至出现减小趋势，当流体比焓进一步升高至接近拟临界比焓，主流流体和近壁面流体密度差减小，浮升力影响减弱，换热系数恢复增大的趋势；热流密度越大，换热系数发生突变所对应的比焓越低，减小的幅度越剧烈，恢复增大趋势后的换热系数也越小。

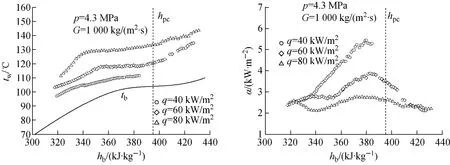
图2 热流密度对壁面温度和换热系数的影响Fig.2 Effect of heat flux on wall temperature and heat transfer coefficient

2.2 质量流速的影响

在压力4.3 MPa、热流密度60 kW／m2的一组典型工况中，质量流速对传热特性的影响规律如图3所示。较大质量流速下，近拟临界比焓区的换热系数显著增大，质量流速2 000 kg／（m2·s）下，低比焓区内换热系数是质量流速1 000 kg／（m2·s）下的2倍。小质量流速下，除换热系数峰值大幅降低外，在较低流体比焓时出现了传热的削弱，壁温升高幅度增大。

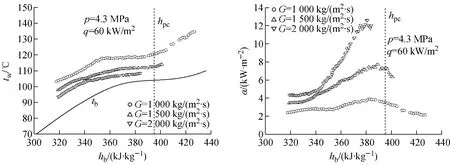
图3 质量流速对壁面温度和换热系数的影响Fig.3 Effect of mass flux on wall temperature and heat transfer coefficient

2.3 压力的影响

在质量流速1 500 kg／（m2·s）、热流密度40 kW／m2时，压力对换热系数的影响示于图4。在远离拟临界点的低焓区，4.3 MPa和4.7 MPa压力下换热系数几乎完全一致；随着流体比焓升高接近拟临界焓，由于近拟临界区的比热更大，4.3 MPa压力下的换热系数相对更大。

3 无量纲数影响分析

图4 压力对换热系数的影响Fig.4 Effect of pressure on heat transfer coefficient

为了定量描述和研究不同热流密度对换热系数的削弱中浮升力的影响，Jackson等［8－9］先后提出了两种表征浮升力影响的无量纲数Bo1和Bo2。Cheng等［10］对于流动方向流体密度梯度和垂直加热面方向密度梯度对超临界对流传热的影响分别提出了加速效应无量纲数πA和浮升力无量纲数πB。

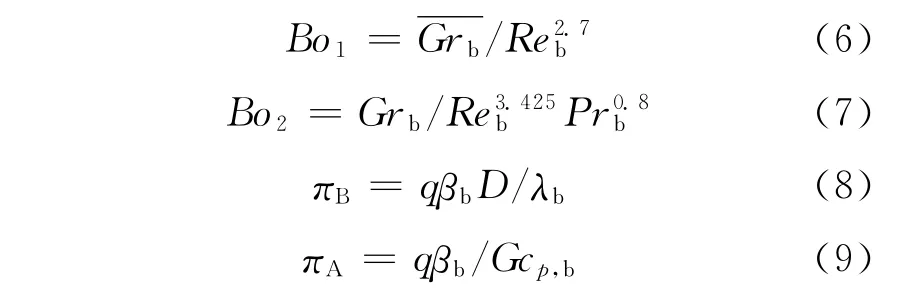
图5示出了试验换热系数α和常物性Dittus－Boelter公式［11］计算换热系数α0的比值和无量纲数之间的关系。可看出，Jackson等［8－9］提出的两种无量纲数对于试验数据未显示出系统的相关性，而Cheng等［10］提出的加速效应无量纲数πA和浮升力无量纲数πB显示了对试验数据很好的相关性。整体而言，当πB增大时，由于近壁面区域速度梯度被减小，湍流强度被削弱，试验换热系数与Dittus－Boelter公式计算值的比值最小可达0.2。主流方向密度梯度的影响更大，πA对换热系数比的影响的单值性更好。当πA较小时，质量流速大、热流密度小、流体比热大，此时加速效应增强换热能力；当πA较大时，主流受加速效应作用的同时，近壁面区域内加速效应更显著，速度梯度造成的剪应力逐步减小，换热被持续削弱。

4 传热恶化起始点

对于各质量流速下发生传热恶化现象的起始热流密度，Yamagata和Styrikovich基于水为工质的试验数据提出了预测关系式。

Cheng等基于无量纲分析，提出以拟临界温度对应的比热和体膨胀系数来体现压力影响的传热恶化预测关系式。对系数修正后，本文得到了适用于氟利昂R134a工质的传热恶化起始点预测关系式。

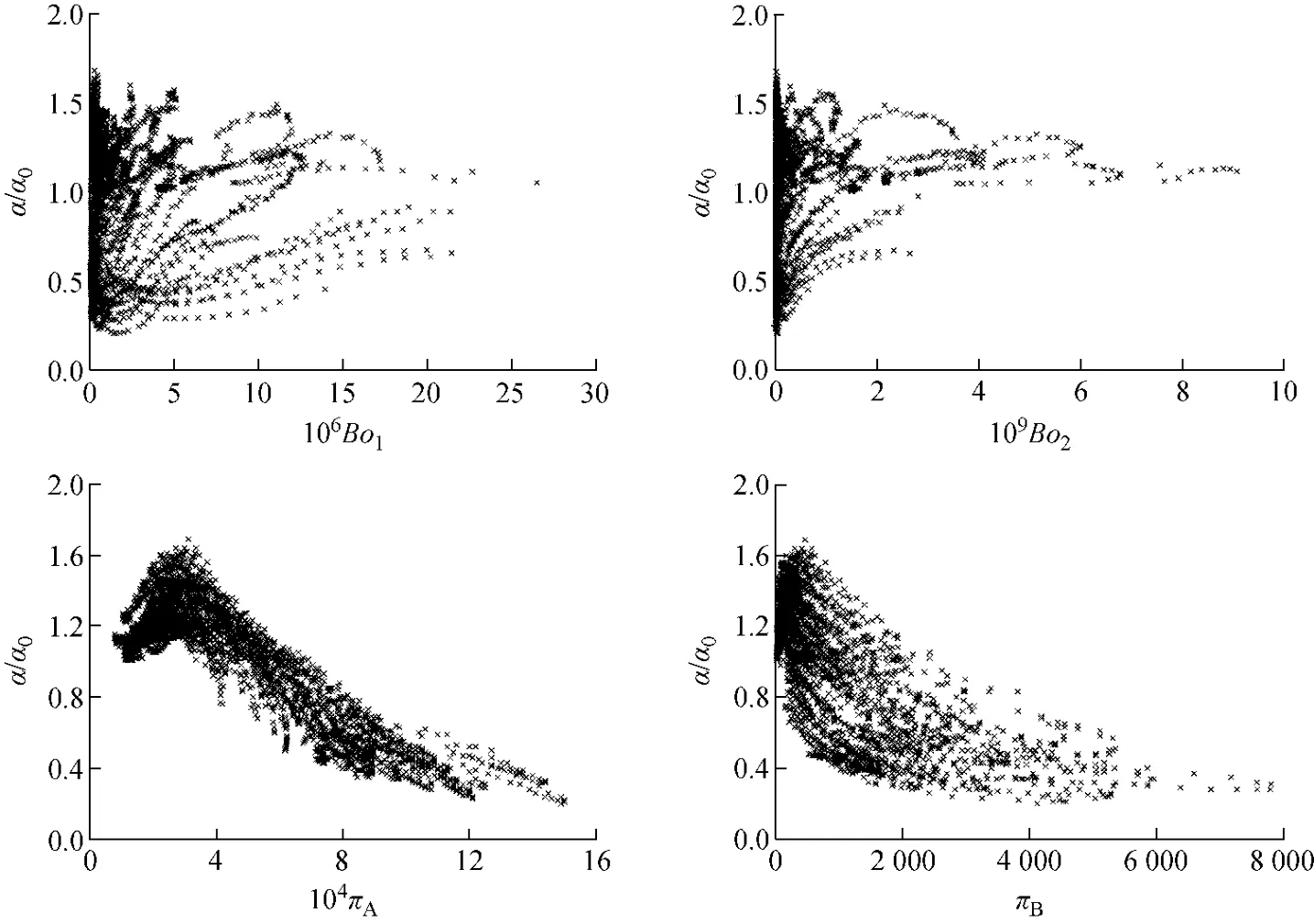
图5 无量纲数对换热系数比的影响Fig.5 Effect of dimensionless number on heat transfer coefficient ratio

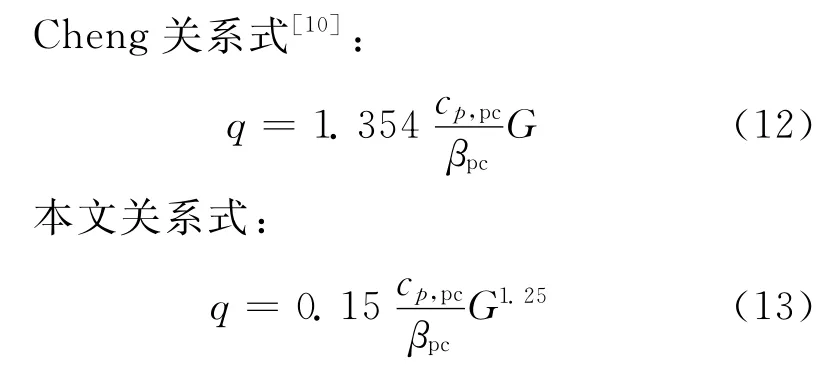
如图6所示，本文提出的预测关系式较好地表达了氟利昂试验数据的规律，适用范围：压力4.3～4.7 MPa，质量流速400～2 500 kg／（m2·s）。

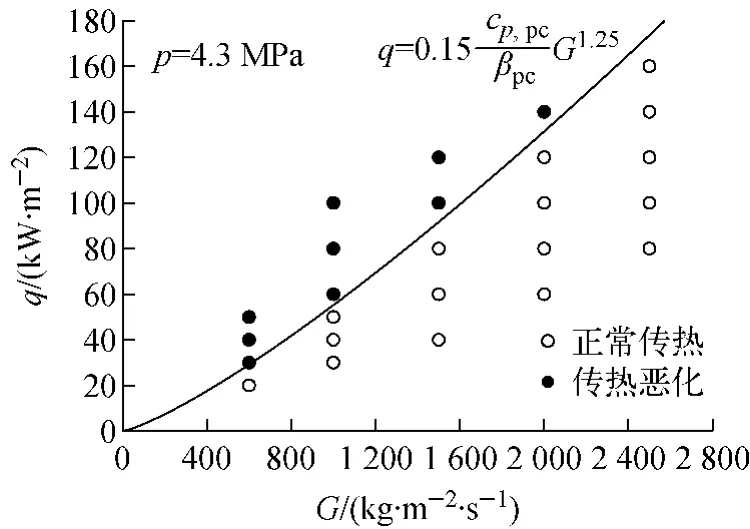
图6 传热恶化起始点预测Fig.6 Prediction of onset of heat transfer deterioration

5 传热经验关系式

由于超临界压力下，尤其是近拟临界温度区内传热的特殊性，各国研究者在超临界流体传热试验数据的基础上，发展出了多种超临界对流换热经验关系式。本文选取两种代表性关系式进行验证，同时以Dittus－Boelter公式作为参照对比。

Bishop关系式［14］：

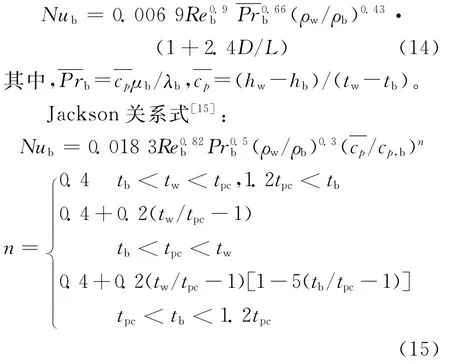
图7和表2为经验关系式计算得到的Nu和试验测得的Nu对比及验证结果。Bishop关系式计算值的集中度最好，标准差为0.097，预测值和试验值之比在1.0～1.8之间，但预测值整体偏大，平均值偏大24.2%。Jackson关系式计算值的平均值和试验值十分接近，仅偏大0.7%，但部分数据点计算的Nu远高于试验值，在小Nu区间尤为明显，计算值和试验值之比最大可达2.3，数据集中度较差，标准差为0.209。

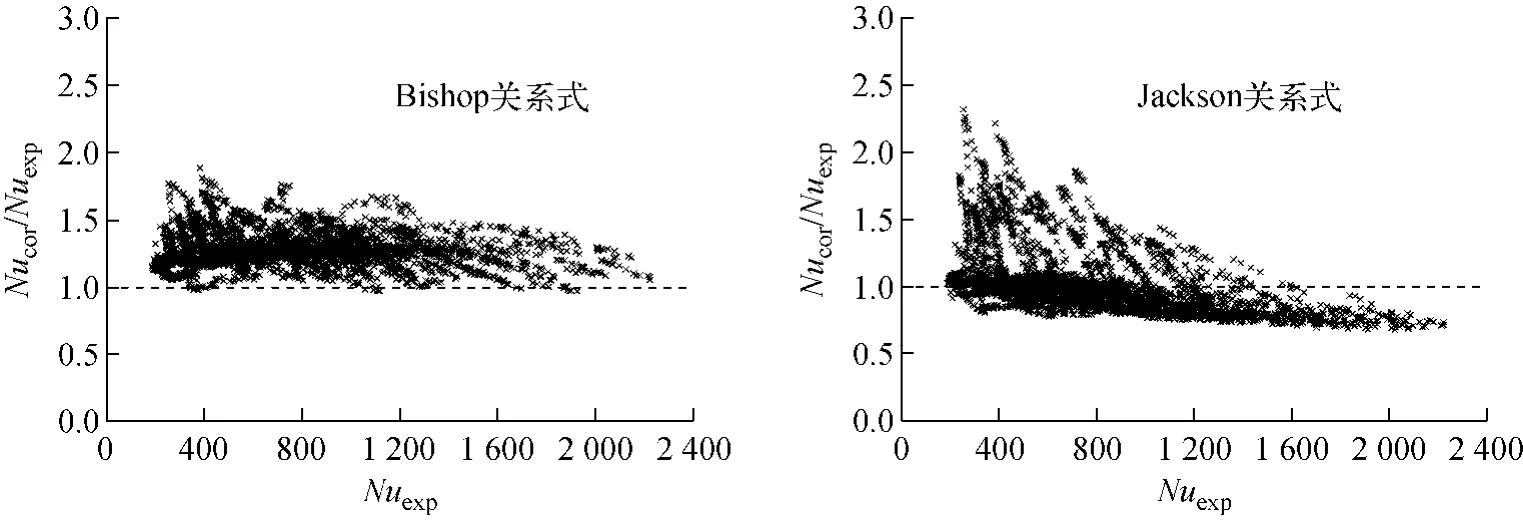
图7 Nu计算值与试验值对比Fig.7 Comparison between calculated Nu and experimental Nu

表2 传热经验关系式验证结果Table 2 Validation result of heat transfer correlations

6 结论

1）低焓区内热流密度对换热系数无影响，近拟临界区内换热系数随热流密度的增大而减小。高热流密度下，在流体焓升高过程中发生换热系数减小现象，热流密度越大，换热系数削弱越强烈，传热恶化发生的焓越低。随流体焓升高，换热系数得到恢复，并在接近拟临界焓处达到最大值。

2）Jackson提出的两种浮升力无量纲数对试验数据未显示出系统的相关性，Cheng等提出的浮升力无量纲数πA和加速效应无量纲数πB对试验数据相关性较好，其中πA的单值性更好，换热系数比随πA从1.0增大到1.7后减小至0.2。

3）参照文献中以水为工质提出的传热恶化起始点预测关系式，提出了适用于氟利昂的传热恶化起始点关系式，与试验数据吻合很好。

4）Bishop关系式计算值和试验值之比的集中度很好，但整体偏大，Jackson关系式计算值的平均偏差很小，但离散度偏大。结果表明，现有经验关系式已有较好的准确性，但仍需进一步改进。

［1］A technology roadmap for GenerationⅣnuclear energy systems［C］∥U.S.DOE Nuclear Energy Research Advisory Committee and the GenerationⅣInternational Forum.US：DOE，2002.

［2］JACKSON J D，COTTON M A，AXCELL B P.Studies of mixed convection in vertical tubes［J］.International Journal of Heat and Fluid Flow，1989，10（1）：2－15.

［3］潘杰，杨冬，董自春，等.垂直上升光管内超临界水的传热特性试验研究［J］.核动力工程，2011，32（1）：75－80.PAN Jie，YANG Dong，DONG Zichun，et al.Experimental investigation on heat transfer characteristics of water in vertical upward tube under supercritical pressure［J］.Nuclear Power Engineering，2011，32（1）：75－80（in Chinese）.

［4］赵萌，李虹波，张戈，等.圆管内超临界水上升、下降流动传热实验研究［J］.原子能科学技术，2012，46（增刊）：250－254.ZHAO Meng，LI Hongbo，ZHANG Ge，et al.Experimental study on heat transfer to supercritical water flowing in circular tubes［J］.Atomic Energy Science and Technology，2012，46（Suppl.）：250－254（in Chinese）.

［5］CHENG X，SCHULENBERG T.Heat transfer at supercritical pressures：Literature review and application to an HPLWR，FZKA 6609［R］.Germany：Forschungszentrum Karlsruhe，2001.

［6］PIORO I L，KHARTABIL H F，DUFFEY R B.Heat transfer to supercritical fluids flowing in channels－empirical correlations（Survey）［J］.Nuclear Engineering and Design，2004，230（1）：69－91.

［7］黄彦平，刘光旭，王俊峰，等.加热工况下圆管内超临界二氧化碳传热关系式分析评价［J］.核动力工程，2014，35（3）：1－5.HUANG Yanping，LIU Guangxu，WANG Junfeng，et al.Evaluation of heat transfer correlations for supercritical carbon dioxide in circular tubes under heating conditions［J］.Nuclear Power Engineering，2014，35（3）：1－5（in Chinese）.

［8］JACKSON J D，HALL W B.Influences of buoyancy on heat transfer to fluids flowing in vertical tubes under turbulent conditions：Turbulent forced convection in channels and bundles［M］.New York：Hemisphere，1979：613－640.

［9］JACKSON J D.Progress in developing an improved empirical heat transfer equation for use in connection with advanced nuclear reactors cooled by water at supercritical pressure［C］∥Proceedings of 17th International Conference of Nuclear Engineering（ICONE17）.Brussels：American Society of Mechanical Engineers，2009.

［10］CHENG X，YANG Y H，HUANG S F.A simplified method for heat transfer prediction of supercritical fluids in circular tubes［J］.Annals of Nuclear Energy，2009，36（8）：1 120－1 128.

［11］DITTUS F W，BOELTER L M K.Heat transfer in automobile radiators of the tubular type［M］.Berkeley：University of California，1930：443－461.

［12］YAMAGATA K，NISHIKAWA K，HASEGAWA S，et al.Forced convective heat transfer to supercritical water flowing in tubes［J］.International Journal of Heat and Mass Transfer，1972，15（12）：2 575－2 593.

［13］STYRIKOVICH M A，MARGULOVA T K，MIROPOL’SKII Z L.Problems in the development of designs of supercritical boilers［J］.Thermal Engineering，1967，14（6）：5－9.

［14］BISHOP A A，SANDBERG R O，TONG L S.Forced convection heat transfer to water at nearcritical temperatures and supercritical pressures：PartⅣ，WCAP－2056［R］.Pittsburgh，USA：Westinghouse Electric Corporation，1964.

［15］JACKSON J D.Consideration of the heat transfer properties of supercritical pressure water in connection with the cooling of advanced nuclear reactors［C］∥Proceedings of 13th Pacific Basin Nuclear Conference.Shenzhen，China：［s.n.］，2002.

Experimental Study on Heat Transfer of Supercritical Freon Flowing in Vertical Tube

ZHANG Si－yu1，2，CHENG Xu1，GU Han－yang1
（1.School of Nuclear Science and Engineering，Shanghai Jiao Tong University，Shanghai 200240，China；2.Nuclear and Radiation Safety Center，Ministry of Environmental Protection，Beijing 100082，China）

The in－depth study on heat transfer characteristics of fluids under supercritical pressure is crucial to the core design of supercritical water－cooled reactor（SCWR）.Heat transfer experiments of supercritical Freon R134a flowing upward in a circular tube were carried out with pressure of 4.3－4.7 MPa，mass flux of 600－2 500 kg／（m2·s）and heat flux of 20－180 kW／m2.The heat transfer coefficient is close to the value calculated by Dittus－Boelter correlation in the region far from the pseudo－critical temperature.However，it is much smaller than the value calculated by Dittus－Boelter correlation with larger heat flux in the region approaching pseudo－critical temperature.The heat transfer deterioration occurs at the condition of small mass flux and large heat flux.It is shown that the heat transfer coefficient is of significant relevance with both acceleration effect dimensionless number and buoyancy dimensionless number.The correlation of onset of heat transfer deterioration is proposed based on experimental data.The heat transfercoefficient calculated by Bishop correlation shows a small standard error but an overall overestimate.The value calculated by Jackson correlation shows a small average error but a larger standard error.

supercritical heat transfer；heat transfer coefficient；heat transfer correlation；dimensionless number；heat transfer deterioration

TL33

：A

：1000－6931（2015）12－2150－07

10.7538／yzk.2015.49.12.2150

2014－09－15；

：2014－11－13

国家自然科学基金资助项目（51206106）

张思宇（1987—），男，天津人，工程师，博士，核能科学与工程专业