一种甘蔗捆绑机的设计与可靠性研究

范 雨，蔡敢为

（广西大学 机械工程学院，南宁 530004）

0 引言

我国的甘蔗产量虽居于世界第三位[1]，但是事实上我国仅是甘蔗产量大国，并非强国，其中重要的原因之一就是我国甘蔗产业的机械化的发展受到了阻碍[2]。甘蔗的捆绑包装是收获过程中的重要环节，而现有的针对甘蔗的捆绑包装机械还是比较稀少而甘蔗尺寸和重量都较一般农产品大，上下料困难[3]。基于以上分析，甘蔗捆绑机处于产品进化过程S曲线[1]的技术改进阶段的前期，将有很大的改进空间。本文首先介绍了这种甘蔗捆绑机的初步设计及工作原理，然后针对主要的零部件进行可靠性分析。

1 甘蔗捆绑机的设计原理

1.1 甘蔗捆绑机的设计思路

在对甘蔗进行捆绑包装之前，首先要对甘蔗进行装载，考虑到甘蔗的生产的收获阶段主要是利用甘蔗收获机完成的，那么，采取直接将甘蔗收获机或甘蔗装载机将收获完成的甘蔗装载到所设计的甘蔗捆绑机的方案，而不是用人力或借助于其他机械设备对甘蔗进行装载，所采取的这种方案将会大大提高工作效率；装载完成后要对甘蔗进行捆绑包装，这部分也是本文所要设计的主要部分；包装完成后要对已经捆绑好的甘蔗进行卸载，为了方便，节省人力，仍然采用利用甘蔗自重作用，采用底卸式[5]方案，直接卸载到拖运小车的车厢内，由拖运小车运走并进入下一个工作环节。为了制糖方便，绿色无污染，捆绑机所采用的绳子为麻绳[2]。设计的甘蔗捆绑机如图1所示。

图1 甘蔗捆绑机完整装配图

1.2 甘蔗捆绑机机架及料斗的结构设计

根据以上设计思路，机架和料斗的结构设计最好是能够让甘蔗“自适应”地、整齐地进入料斗。料斗的开合由可控的液压缸驱动的，实现甘蔗的装载与卸载，平稳可靠，也适应甘蔗地的工作现场。

1.3 甘蔗捆绑机的捆绑机构的设计

甘蔗装载的下一道工序就是要对甘蔗进行打捆包装。实际上，在甘蔗装载之前，要把绳子摊开，待甘蔗装载后，还要把绳子两端合拢，进一步完成打结操作；打结完成之后，要对绳子进行割断操作。因此，为了完成上述任务，分别需要设计送绳机构、打结机构和剪绳机构。

为了完成绳子的“递交”任务，设计了如图2(a)所示的送绳钳。传动轴与可动钳块之间通过旋向相反的螺纹相连，实现钳块的加紧与松开。送绳钳整体安装在主托板上。为了完成绳子的“接受”任务，设计绳夹机构，如图2(b)所示。绳夹两侧通过压紧弹簧压紧。送绳钳夹持着绳子向前运动，便将绳子“挤入”绳夹中。与此同时，分别位于两个托板下边的绳槽将绳子聚拢。于是，上有绳夹固定的双根绳子与下边的绳槽聚拢的双根绳子合叠在一起，形成贯穿上下的拉直状态，为下一步的打结做好准备。绳夹机构整体安装在副托板上。绳夹机构的设计简便易行，巧妙地减少了动力源个数。

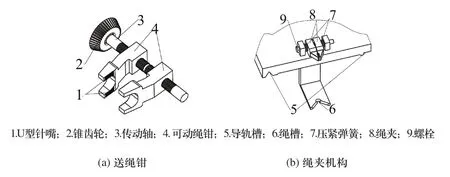
图2 送绳钳与绳夹机构

根据人单手对绳子进行打结的姿势和动作原理，类比设计了打结机构，如图3所示。钳头的设计即是模拟人单手对绳子打结过程中所使用的食指和拇指，对绳子的咬紧与放开通过凸轮及拉紧弹簧的配合加以实现。

图3 打结机构

对绳子打完结后，要对绳子进行剪断处理。为了实现这个目标，设计了如图4所示的剪断机构。由主动轮、矩形滑块以及回字形推杆组成的正弦机构[3]实现剪刀的剪绳操作。

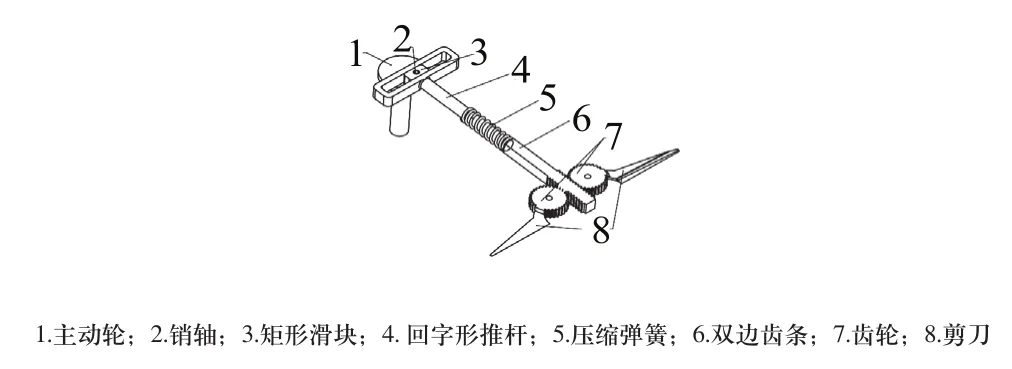
图4 剪绳机构

如图5所示是甘蔗捆绑机的主要机构的装配图。

图5 主要机构装配图

2 绳钳的可靠性研究

2.1 最大应力截面的确定

首先，确定绳钳的最大应力截面，及危险截面。上钳额在工作过程中，勾住绳子拉住绳子时是其工作周期中承受拉力最大的环节。实际上，绳子勾住的位置为下钳颚的根部，这时钳口是紧闭的，那么压力就会均匀分布在上钳颚的齿面上。

甘蔗的密度为1067kg/m3[8]，按照甘蔗的平均长度2m，直径为0.04m，每捆甘蔗20根作为本机的设计要求。拉住绳子打结过程中，绳子与竖直方向的夹角为20°计算。为了保险起见，绳钳的拉力至少为：

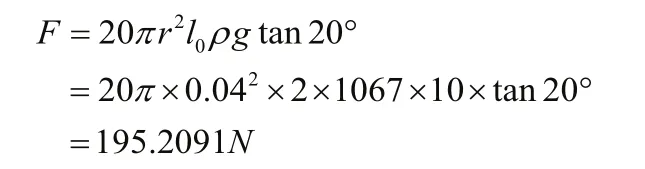
夹嘴面积为217mm2。初步计算钳口上的均布载荷为0.8986Mpa。绳钳的材料采用碳素结构钢Q215A，屈服强度为205Mpa，抗拉强度为335Mpa～450Mpa，弹性模量为2×105Mpa，剪切模量76923Mpa，泊松比为0.3[9]。

由于打结机构速度较低，故通过有限元分析软件Workbench采用静力学分析确定危险截面的位置。如图6所示。

图6 Workbench应力分析

由图6可以看出危险截面位于上钳颚与侧帮相接的截面位置。

2.2 应力的求解

根据图7所示的形状尺寸，进行受力分析，如图所示。

图7 上钳颚的形状与尺寸

若绳子对绳钳的拉力为F，则均布应力为：

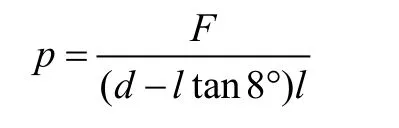
那么危险截面的最大正应力为：

结合第四强度理论[4]：σ-τ的复合应力表达式为[11]：

应力集中系数Kα与组合应力集中系数Kαc实际计算不会相差很大，故一般就用应力集中系数计算即可[12]。

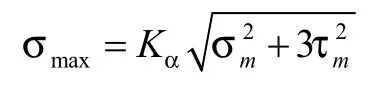
2.3 基于Monte Carlo[13]方法确定应力分布

由于甘蔗的直径和长度是随机的故导致拉力F也是随机的。一般而言，甘蔗的半径和长度均服从正态分布，其他形状尺寸均服从正态分布。则有：

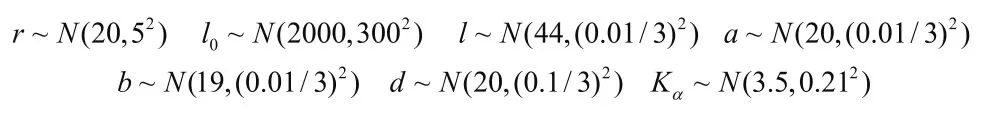
Monte Carlo模拟方法的步骤为：

然后，对每一个随机变量Xi(i=1,2,…,7)在(0,1)上生成N个随机数pij(j=1,…,N)，作为随机变量各自的概率分布函数Fi(Xij)的值；

3) 计算应力。将每一次模拟得到的随机数值代入式(1)中，进行求解；

σmaxj=g(X1j,X2j, … ,X7j) （j=1,…,N）。然后求解应力样本函数随机值的均值和标准差；

4）通过MATLAB做出应力函数随机值的频数分布直方图（如图8所示），并拟合其分布。

图8 频数分布直方图

对于分布的Monte Carlo模拟方法的求解，存在着求解精度与抽样次数之间的矛盾[15]。图8是在选择的抽样次数为100000次的情况下求得的结果。并得到的样本均值和标准差为：。

通过观察，与伽玛分布比较接近。并利用MATLAB的dfittool拟合工具箱采用gamma在可信度为99%时进行拟合。拟合结果如图9所示。

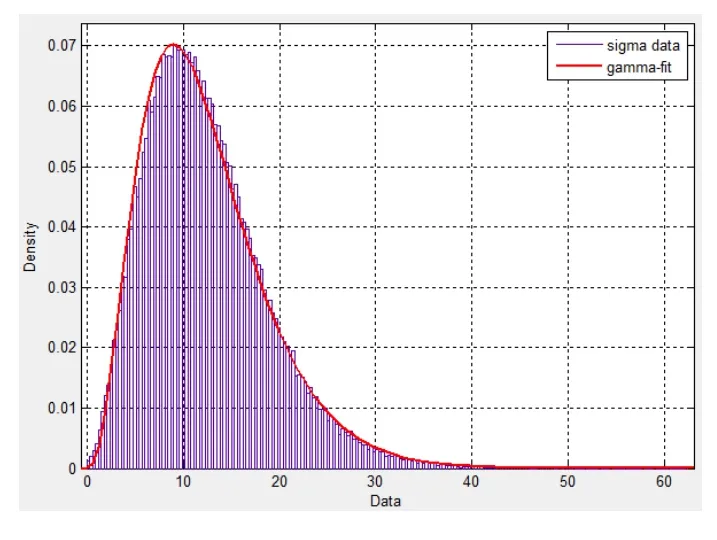
图9 伽玛分布拟合

2.4 可靠度的计算

根据经验资料初步判断其强度的分布为正态分布：

首先采用数值积分法求解失效率。具体方法是，首先在统计范围内将横轴x进行n等分，图10为二者概率密度函数图像。于是有：

图10 概率密度函数图像

由此可见，该绳钳的上钳颚设计具有足够的可靠度，完全满足要求。

3 结束语

本文首先分析了甘蔗收获过程中的一些特点，结合实际工作情况，然后根据要完成的工作任务和待解决的矛盾逐一确定基本设计思路，进而完成一种甘蔗捆绑机的设计。其突出优点在于：收获甘蔗的同时，依靠已经收获好的甘蔗自身重力落入料斗内，完成捆绑工作后，利用甘蔗自身的重力采用底卸式进行卸料装载；打结机构设计与布置结构紧凑；本捆绑机所采用的绳子的材料采用麻绳，因为麻绳的主要成份是纤维素，绿色无毒制糖过程中无需解下分离。然后，对其关键的零部件绳钳的上钳颚进行了可靠性分析，分析结果显示：绳钳的设计完全满足可靠性设计要求。但是后续工作还需对其他关键的零部件进行可靠性分析，进而综合得到系统的可靠性，然后通过调整设计所要研究的各个随机变量来实现总体可靠度的要求。

[1] 潘侃,范雨,温芳.一种甘蔗捆绳机的运动学与静力学研究[J].装备制造技术,2014(08).

[2] 李海福.广西甘蔗生产现状及对策研究[D].2012,广西大学:南宁.

[3] 耿葵花,蔡敢为,范雨,等.一种甘蔗捆绳机:中国,CN103703941A[P].2014-04-09.

[4] 檀润华.创新设计:TRIZ:发明问题解决理论[M].北京:机械工业出版社,2002.

[5] 薛河.底侧卸式矿车最佳卸载曲轨线初探[J].煤矿机械, 1989(10):9-10.

[6] 蔡敢为,范雨,耿葵花,等.一种甘蔗捆绑机:中国,CN103703937A[P]. 2014-04-09.

[7] 蔡敢为,范雨,等.一种摇篮机构:中国,CN103829661A[P].2014-06-04.

[8] 陈永继.甘蔗—土壤系统仿真模型的研究[D].广西大学,2008.

[9] 成大先.机械设计手册（第五版）[M].北京:化学工业出版社,2008.

[10] 刘鸿文.材料力学I（第五版）[M].北京:高等教育出版社,2004.

[11] 陈四利.第三强度理论与第四强度理论的统一表达式[J].力学与实践,1997(04).

[12] 航空工业部科学技术委员会.应力集中系数手册[M].北京:高等教育出版社,1987:16.

[13] C.L.T. Borges, D.M. Faleao, J.C.O. Mellon.Composite reliability evaluation by sequential Monte Carlo simulation on parallel and distributed proeessing environment[A].IEEE Transactions on Power Systems[C].2001,6(2).

[14] 杜书华.输运问题的计算机模拟[M].长沙:湖南科学技术出版社,1989.

[15] 刘惟信.机械可靠性设计[M].北京:清华大学出版社,1996.