航空发动机典型转子件装配偏差建模及分析
单福平,李志敏,朱 彬
(1.上海交通大学 上海市复杂薄板结构数字化制造重点实验室,上海 200240;2.中航商用航空发动机有限责任公司,上海 201108)
0 引言
航空发动机转子在高温、高压环境中高速旋转,转子装配的不同心对转子的初始不平衡量和转静子碰磨等具有严重的影响,最终会影响整机的振动表现和性能表现,因此要求转子有非常高的装配精度[1, 2]。以某型高压压气机转子装配为例,要求篦齿盘后止口端面跳动、柱面跳动均不大于0.03mm[2]。
为了满足装配精度的要求,在设计及制造过程中必须考虑形位偏差的影响。而现有的研究工作往往将转子装配特有的止口结构简化,并没有阐明形位偏差的传递机理[1, 3, 4]。另外,在以往的研究中,使用最广泛的误差分布函数是正态分布,但这种假设并不一定有效,由于系统误差、刀具磨损等各种客观因素的存在,非正态分布、不对称分布应该是更为合理的选择[5]。
针对上述问题,本文考虑航空发动机转子零部件特有的止口装配结构,建立了包含尺寸偏差和形位偏差的刚性尺寸链模型。并进一步结合皮尔逊分布族,研究了各偏差在不同的概率分布模型下对最终装配质量的影响。最后,将该方法与蒙特卡罗模拟法进行对比,以验证方法的有效性。
1 尺寸链建模
航空发动机转子为回转结构,其典型零件是盘和鼓,装配过程就是盘和鼓的堆叠。当零件加工制造过程中产生误差时,装配后的转子部件就会产生不同心度。由于转子零件是空心的,实际测量中往往采用测量径向跳动来代替,如图1右侧所示。零件之间的连接方式是止口加螺栓连接,其中止口端面和柱面起定位作用,轴向均布的螺栓用于压紧端面从而传递扭矩,止口为过盈配合,如图1左侧所示。
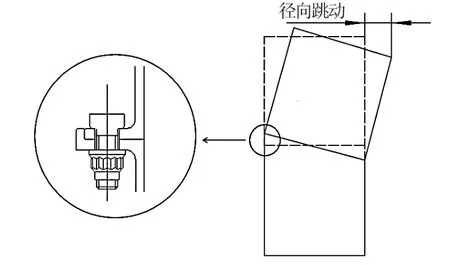
图1 径向跳动测量及止口配合
假定转子部件由n个零件装配而成,装配顺序从下往上,在第一个零件的下止口建立全局坐标系,规定X方向为轴向,Y方向为径向。测量要求为最后一个零件的上止口圆柱面的径向跳动量。其中第i个零件的尺寸及偏差如图2所示,由于轴向的尺寸偏差对测量的径向偏移可以忽略不计,故图中没有标注。
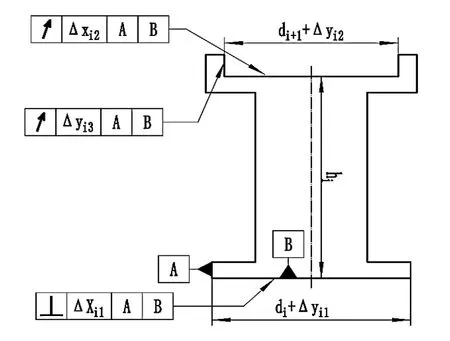
图2 第i个零件的尺寸及偏差标注
通常装配基准的选择应该以较大的平面作为装配主基准面。转子零件止口装配处,由于柱面很短,端面面积要远大于柱面面积,所以在转子零件的装配过程中,止口端面为装配主基准。根据文献[6]中描述的方法可知,在平面与平面配合时,若其中一个平面上存在跳动偏差,那么该偏差会引起另一个平面的平移和转动,平移量为偏差的带宽,转动角的正切值为偏差带宽与特征长度的比值。因此,止口处的跳动偏差会导致零件2产生绕Z轴的转动,以及垂直于配对平面的平移。由于止口端面为装配主基准,并且在航空发动机转子的实际装配中,通过螺栓拧紧保证了止口端面的紧密贴合,故绕Z轴转动的角度应该由端面的跳动偏差决定,如图3所示。跳动偏差在端面产生的平移方向为轴向,对测量径向偏移几乎无影响,在此不作考虑。止口柱面上的跳动偏差产生的平移为径向,需要考虑。

图3 端面跳动引起的零件偏转和平移
综上所述,在止口配合中,端面上的跳动偏差引起了装配件绕z轴的转动,圆柱面上的跳动偏差引起了装配件的径向平移。例如的贡献为同样的,的贡献机制也是如此(忽略产生的偏转角的影响)。故:
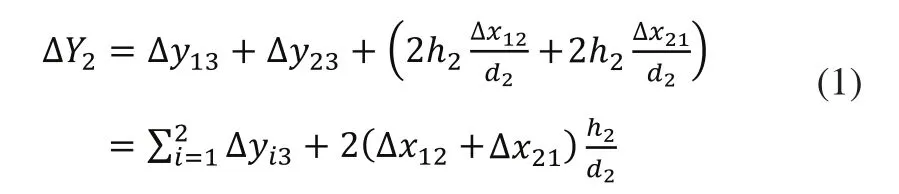
以此类推,当三个零件装配时,

当n个零件装配时,
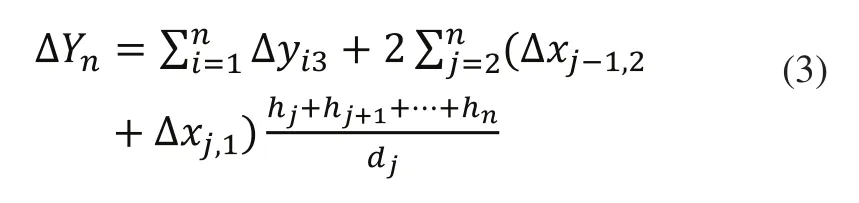
2 求解方法
由于机械零件在加工制造过程中存在各种各样的系统误差和随机误差,往往导致零件的尺寸与形位偏差的概率分布并非理想的正态分布。为了提高装配精度,必须考虑概率分布类型的影响。目前普遍采用蒙特卡罗法来模拟不同的概率分布,但是蒙特卡罗法要达到较高的精度,必须模拟几十万乃至上百万次,计算效率很低。故本文引入了皮尔逊分布族的方法,该方法相较于蒙特卡罗法能极大地提高计算效率。
皮尔逊分布族包括正态分布,也包括许多偏态分布,其概率密度函数f(x)决定于微分方程:

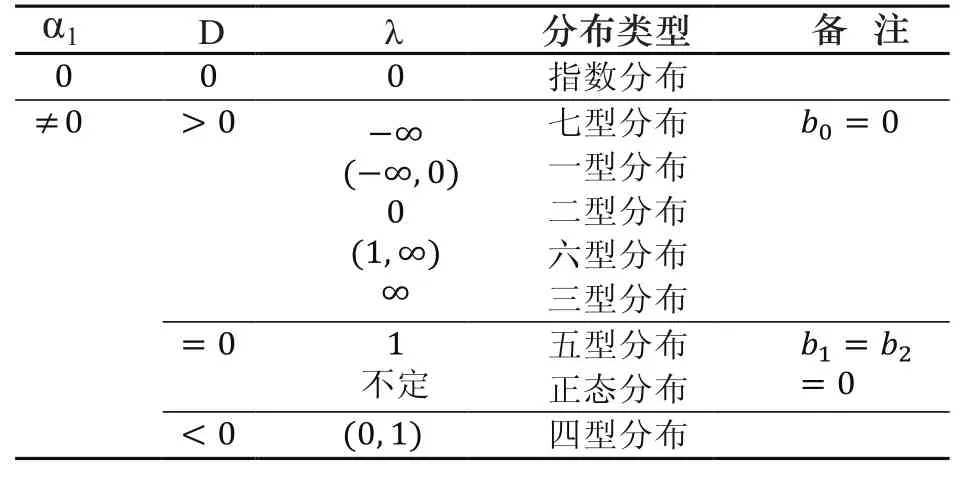
表1 皮尔逊分布类型的判别
根据皮尔逊分布族的特点,只需要求得某一分布的前四阶中心矩,即可判断其属于何种分布并确定概率密度函数。对于任意分布,一阶中心矩恒为零;二阶中心矩即方差,反映了数据的离散程度;三阶中心矩与偏度系数S相关,它们之间的关系为四阶中心矩与峰度系数相关,它们之间的关系为由于概率分布的均值、方差、偏度和峰度能够较直观的反映分布的形态,因此,本文通过计算这四个参数来间接计算分布的前四阶中心矩。各种分布类型的均值、方差、偏度系数和峰度系数的计算公式可参照文献[7]。
假设各个组成环偏差为任意分布且相互独立,则可通过组成环偏差分布的四个参数求得封闭环分布的四参数。
封闭环的分布参数计算如下:
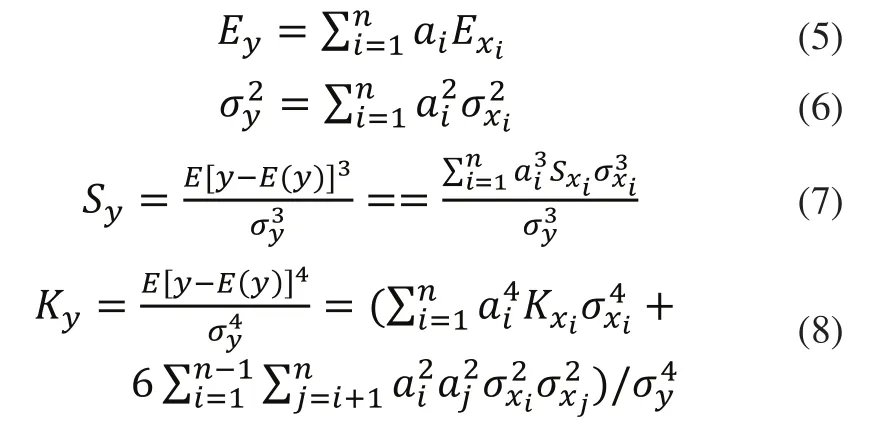
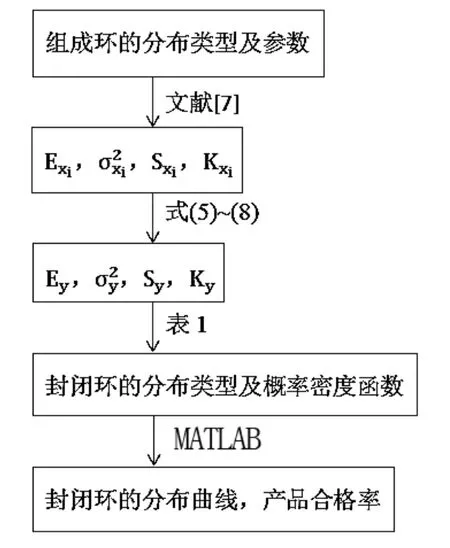
图4 求解与分析流程
3 实例分析
已知某型航空发动机转子其中两个零件的尺寸及公差如表2所示。根据式(1)可求得误差传递函数为该装配体的径向跳动要求为0.03mm,即满足。
机械加工过程中常见的分布类型有正态分布,偏态分布,均匀分布(平顶分布)等[8],我们假设组成环偏差的分布类型分别服从这几种常见分布,设计了四种组合方式来验证概率分布类型对最终装配偏差的影响,其中偏态分布使用Beta分布进行模拟,如表3所示。
按照公式(5)~式(8)计算得到封闭环偏差分布的参数如表4所示。再使用MATLAB计算四种情况下装配后的合格率,并与蒙特卡罗模拟(1000000次)的结果进行对比,结果如表5所示。绘制了封闭环偏差分布曲线(本文方法)及柱状图(蒙特卡罗法),如图5所示。

表2 零件尺寸及公差(单位:mm)

表3 各组成环的分布类型及参数
通过将本文方法的计算结果与蒙特卡罗模拟的结果进行比较,可以发现:图5中用本文方法绘制的曲线和用蒙特卡罗法绘制的柱状图吻合的相当好,表5中两种方法计算的合格率误差也不超过0.5%,证明本文提出的方法与蒙特卡罗法精度相当。而本文方法只需计算一次,蒙特卡罗法需
要计算一百万次,本文方法极大地提升了计算效率。
另外从图表中还可以看出:当组成环的公差带不变,而分布类型发生变化时,封闭环的分布形态与零件装配的合格率会有相当大的变化,在本文的四组实验中合格率最大变化超过了50%。
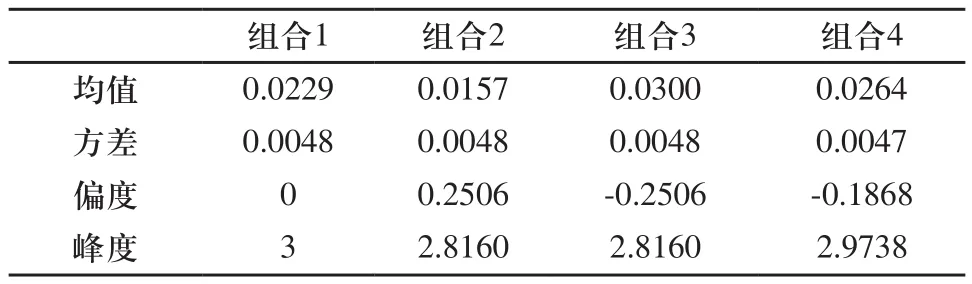
表4 封闭环偏差分布参数

表5 四种组合的合格率对比
4 结论
本文阐明了形位偏差在航空发动机典型转子件止口装配过程中的传递机理,建立了一般化的尺寸链模型。
通过实验对比,本文介绍的方法与蒙特卡罗模拟一百万次的计算精度相当,并且计算效率要远远高于蒙特卡罗法。
将实际制造过程中经常出现的偏态分布与正态分布的假设进行对比,计算结果表明零件制造偏差的概率分布类型对最终装配偏差有很大的影响,传统的正态分布假设无法还原真实情况。因此,在航空发动机转子设计阶段必须结合实际的加工工艺确定偏差的分布形态,才能使得设计结果更加合理。
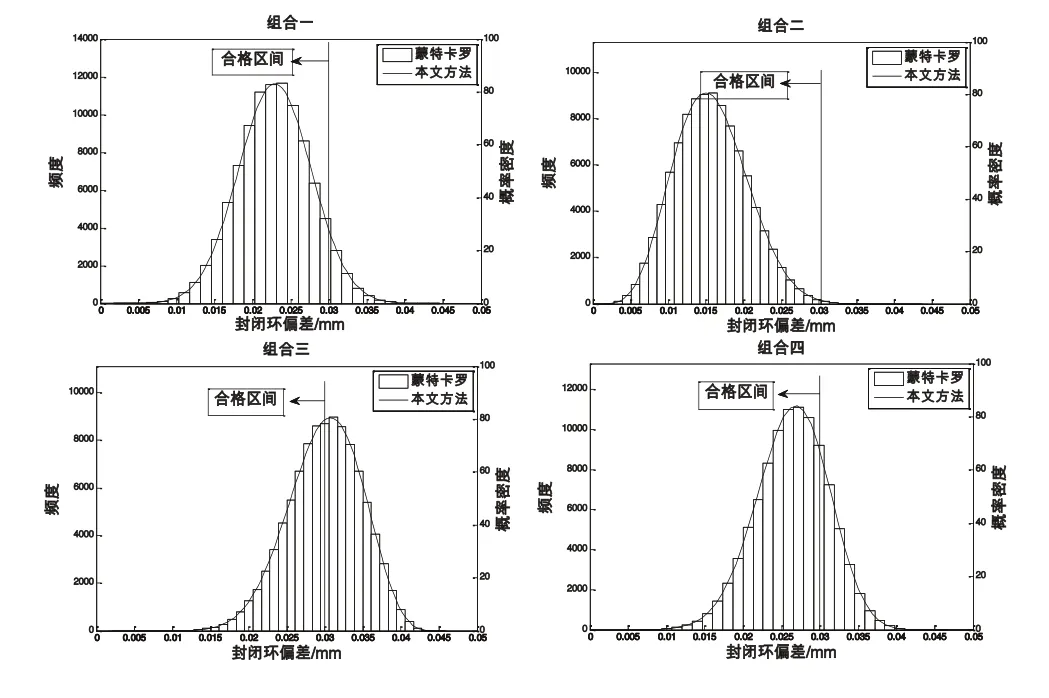
图5 封闭环偏差分布曲线及柱状图
[1]刘君,吴法勇,王娟.航空发动机转子装配优化技术[J].航空发动机.2014, 40(3):75-78.
[2]史新宇,吕玉红,吴法勇.整机装配阶段的同心度测量研究现状综述[A].中国科协年会: 航空发动机设计、制造与应用技术研讨会 [C]:2013.
[3]王晶,石宏,黄笑飞,等.基于蒙特卡罗模拟法的航空发动机装配公差分析[J].沈阳航空工业学院学报.2010,27(4):8-11.
[4]Hussain T, Yang Z,Popov A A,et al.Straight-Build Assembly Optimization: A Method to Minimize Stage-by-Stage Eccentricity Error in the Assembly of Axisymmetric Rigid Components (Two-Dimensional Case Study)[J].Journal of Manufacturing Science and Engineering.2011, 133(3):31014.
[5]杨慕升.统计公差技术及其在制造过程质量控制中的应用研究[D].南京理工大学,2009.
[6]Chase K W, Gao J,Magleby S P.Including geometric feature variations in tolerance analysis of mechanical assemblies[J].1996.
[7]Johnson N L, Kotz S, Balakrishnan N.Continuous Univariate Distributions; Volume 1[J].1994.
[8]卢秉恒.机械制造技术基础[M].北京:机械工业出版社, 2005.

