无线传感网大空间定位测量算法及精度评估
刘文文,王俊岭,杨 瑛
(合肥工业大学,合肥 230009)
0 引言
无线传感网络的很多应用都涉及距离位置信息,基于无线传感网络的大空间定位技术也因此成为这一研究热点的关键基础技术。无线传感网络定位技术有基于非测距定位技术和基于测距定位技术,基于测距的定位技术分为基于信号接收强度指示值测量(RSSI)方法、基于到达时间测量(TOA)方法以及基于时间差测量(TDOA)等方法等。本文对基于时间差的测量方法(TDOA)进行分析研究和仿真,面对距离测量精度和范围的限制,寻找高精度的定位算法,面向无线传感网络结构参数通过仿真评估大空间定位精度。研究对设计满足一定定位精度的无线传感网络具有指导意义。
1 原理分析及算法
基于距离测量的大空间定位方法通过测量移动节点到信标节点的距离实现移动节点的空间定位,高精度定位的关键点在于高精度的距离测量方法及高精度的定位算法。
假设在移动节点P(x,y,z)周围有n个位置已知的信标节点G1(x1,y1,z1),G2(x2,y2,z2),…, Gn(xn,yn,zn)参与测量,如图1所示,它们与移动节点的距离的测量值为D1,D2,…,Dn,而理论距离为:
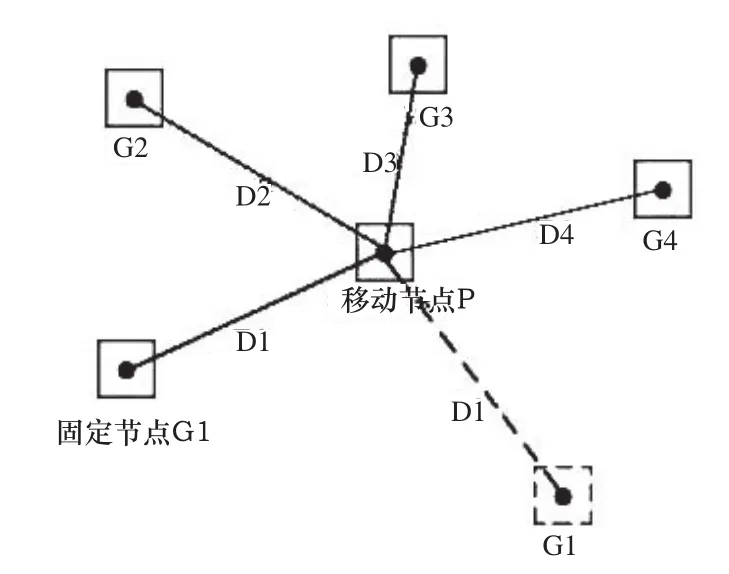
图1 移动节点与信标节点

以测量距离与其理论值的残余误差平方和最小为原则定位移动节点P(x,y,z),则测量模型为:
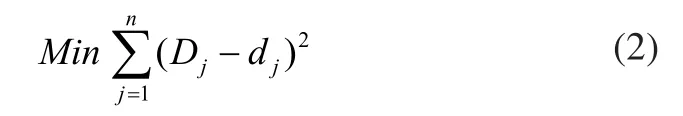
这是一个无约束非线性优化问题,理论上可以用非线性无约束优化方法求解[1]。在此,笔者提出一种线性迭代算法求解该非线性优化问题。

设方程组(3)的极大似然估计解为P0(x0,y0,z0),则有:

其中:
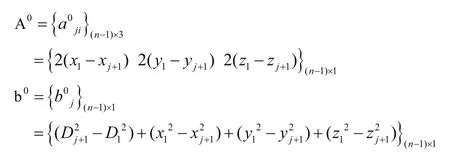
把移动节点近似解P0(x0,y0,z0),带入式(1)有:

将式(1)在P0处作一阶泰勒展开处理,有:
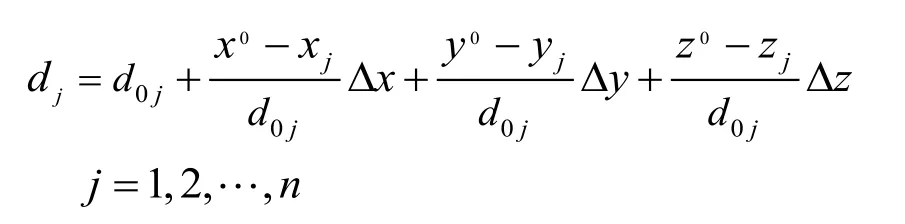
带入式(2),则式(2)转换成无约束的线性最小二乘问题,那么,其解为[2]:

其中:

因此,得移动节点的新定位坐标P1(x1,y1,z1),为将P0和P1分别带入式(2)计算两者残差平方和之差,如果满足收敛条件(即残差平方和之差的绝对值小于e),则停止计算,P1则为式(2)的最优解;否则赋值P0=P1,进行新一轮迭代。该算法通过迭代线性最小二乘问题来求解非线性最小二乘问题,求解精度高于传统方法。
2 选择性定位算法分析
基于TDOA的定位方法使用两种传播速度不同的无线信号(电磁波和超声波)实现移动节点到信标节点的距离测量。假设移动节点在T0时刻同时发射超声波和电磁脉冲信号,某信标节点在T1、T2时刻分别接收到无线脉冲信号和超声波信号,得移动节点到信标节点之间的测距公式为:
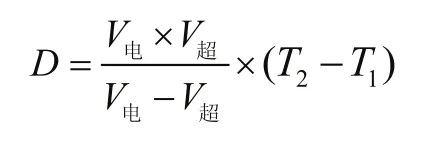
超声波在20℃环境下传播速度约为V超=344m/s、电磁波传播速度约为V电=3×108m/s,两者相差巨大,从而测距公式可以简化为:


图2 移动节点测距信号的覆盖区域
由此带来的测量误差在百米范围内小于0.1mm。因此,所谓基于到达时间差的测距定位方法简化后就是超声波测距定位法,而电磁波信号的作用仅仅是确定超声波发射的时间。超声波换能器具有较好的方向性和额定的发射功率,这些因素限制了超声波覆盖角度和可测距离范围。假设超声波最大测距范围为Dmax、覆盖角度为θmax,若移动节点发射测距信号,距离可测区域为以其自身为中心、正传播方向为轴线、θmax为锥角、Dmax为半径的锥球体,如图2所示。因此,参与移动节点定位测量的信标节点是有选择性的,只有那些位于移动节点发射信号覆盖区域内的信标节点才能参与移动节点的定位测量,故移动节点的定位测量模型为:


这是一个有约束非线性优化问题,算法类似于无约束定位算法,只是添加信标节点选择模块,算法流程如图3所示。
在基于距离测量的空间定位技术中,任何测量原理都存在着测量距离和角度的约束,因此笔者提出的选择性定位算法不仅可以用于超声波测距定位,也可以用于其他无线传感网大空间定位测量,只需要更改约束参数即可。

图3 选择性定位算法框图
3 空间定位精度分析
项目采用激光测距技术实现高精度超大空间坐标测量定位;采用无线传感网TDOA定位测量技术实现激光靶镜初定位,以引导激光跟踪,因此要求无线传感网定位实现激光靶镜的正确定位,确保激光光束不脱靶。系统构架是:移动节点实现无线信号发射、信标节点接收无线信号,采用的超声波换能器发射波束角60°最大探测距离15m。经过测试实验,超声波最大测距范围为10m;覆盖角度为±30°。实验测得在此范围内超声波距离测量标准差为[2]。

其中:

在此,σ和D以mm为单位、θ以rad为单位。那么,面对移动节点特定的定位空间要求50m×50m×10m以及定位精度±35mm要求,研究信标节点网络配置算法是十分必要的。
1)蒙特卡洛仿真模块
蒙特卡洛方法又称为随机事件模拟,随着计算机技术和软件技术的发展,该方法已广泛应用于测量不确定度评定、可靠性分析评估、仪器误差综合和精度分配等领域。其通过对不同分布的抽样来模拟仪器系统参数的随机误差源,引入仪器测量方程后,通过对大量仿真计算结果的统计来评估仪器精度[3,4]。
若某一信标节点位于移动节点P(x,y,z)的覆盖范围,测得距离测量值为Di、与移动节点的角度估计值为θi,带入式(5),获得距离测量的标准差σi。对每一个信标节点,设超声波测距误差服从均值为零、方差为σi(i=1,2,…,m)(如式(5)所示)的正态分布,采用MATLAB命令在该分布中抽样随机数 δi(i=1,2,…,m)来模拟距离测量误差ΔDi,加上距离测量值Di(i= 1 ,2,… ,m)后带入式(4),计算移动节点的定位结果。计算定位误差:

对于某一移动节点,经过K次计算,对计算结果进行统计,统计获得该移动节点的定位误差的标准差。定位精度评估算法框图如图4所示。
2)仿真计算
设信标网络配置如图5所示。其中L表示信标节点间距;low,high表示研究区域的垂直范围;bianch表示研究区域的水平范围,整个研究区域即灰色部分。通过仿真计算萃取研究区域内满足一定定位精度的可定位空间范围。

图5 信标网络配置参数含义
信标网络配置参数如表1所示,面对表1所示的研究空间范围和不大于±35mm的定位误差要求。在研究区域内按照正方体的排列方式,每隔50mm取点计算移动节点的定位精度并把所有满足精度要求的点绘制成三维图。

表1 仿真参数表
图6~图8分别呈现了当信标节点间距L为1m、1.5m和2m时满足定位精度要求的移动节点可定位区域。显然,满足精度要求的移动节点可定位区域随信标节点间距的增加而逐步减小,并且离信标网络越远,水平可定位区域越小。

图6 L=1m时可定位区域
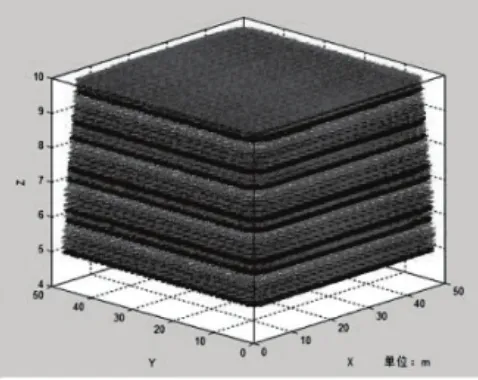
图7 L=1.5m时可定位区域
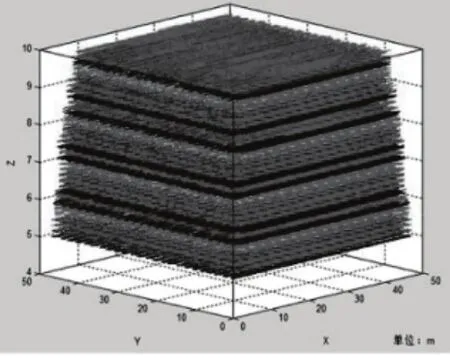
图8 L=2m时可定位区域

图9 同一平面定位精度分布
图9呈现的是当信标节点间距为1m,距离信标节点垂直距离为8m的XY平面上移动节点的精度分布情况,显然定位精度在四个边角区域下降,有相当大的区域定位精度保持一致。
4 结束语
论文面对基于无线传感网大空间定位测量过程中的共性问题:测量距离约束和信号覆盖范围约束,提出了一种选择性大空间定位算法。面对移动节点特定的定位空间要求以及定位精度要求,采用蒙特卡罗方法研究了测距误差、信标网络配置对移动节点可定位空间的作用关系,论文提出的仿真模式对于设计评估满足一定精度要求的无线传感网络定位空间具有一定的指导意义。
[1]赖炎连,贺国平.最优化方法[M].北京:清华大学出版社,2008,12.
[2]胡佳文.基于无线传感网络的空间坐标测量技术研究[D].合肥工业大学,2013.
[3]刘文文,葛乐矣.基于蒙特卡罗方法的虚拟仪器测量不确定度评估[J].电子测量与仪器学报,2007,21(3):56-59.
[4]费叶泰.误差理论与数据处理-第五版[M].北京:机械工业出版社,2004.
[5]孟东阳,何秀凤,桑文刚.基于无线网络传感器的定位技术研究[J].电子测量技术,2012,35(9):4-9.
[6]赵海,张宽,朱剑,等.基于TDOA的超声波测距误差分析与改进[J].东北大学学报,2011,32(6):802-805.
[7]王磊,胡爱群,白光伟.一种传感器网络高精度定位系统设计与仿真[J].计算机工程与应用,2012,48(5):107-109.
[8]Prince Singh, Sunil Agrawal.TDOA Based Node Localization in WSN using Neural Networks[C].2013 International Conference on Communication Systems and Network Technologies,2013:400-404.
[9]Ali Husein Alasiry,Shinji Ohyama.Range-based Localization with the Concept of Virtual Boundary for Wireless Sensor Networks[J].Chinese Journal of Scientific Instrument,2012,33(8):1697-1707.

