基于动态模糊神经网络的并联机器人鲁棒复合控制研究
赫建立,朱龙英,成 磊,殷久诚
(1.常州大学 机械工程学院,常州 213164;2.盐城工学院 汽车工程学院,盐城 224051;3.西安工业大学 机械工程学院,西安 710021)
0 引言
并联机器人具有结构稳定、运动负荷小、微动精度高、末端件惯性小以及快速的动态响应等优点,目前已被很多大型企业用于物品抓取、去毛刺、焊接等对零部件精度要求高的工作场合[1]。但作为被控对象,仅从其动力学观点来分析,其刚体动力学模型是一个高度非线性且具有强耦合性的复杂系统,传统的控制方法已无法对其轨迹跟踪精度进行很好的控制。因此,并联机器人系统的控制问题已成为目前急需解决的问题之一[2]。
由于6-DOF并联机器人结构的复杂性,系统通常会存在参数摄动和外界不确定性因素的干扰问题,导致常规的设计方法已无法满足控制系统的鲁棒性与稳定性等要求。因此为了消除结构模型非线性和负载交联耦合干扰对系统的影响,Kim等[3]设计了一种带有摩擦估计器的鲁棒非线性控制器并将其应用于6-DOF并联机器人中,通过Alpha-beta跟踪器获得了系统的理想状态。赵东亚等[4]对一种6-DOF并联机构进行了非线性的分散鲁棒控制器的设计,运用Lyapunov方法对系统的稳定性进行了分析,并结合SimMechanics仿真验证了其有效性。朱大昌等[5]针对6-RPS型并联机器人的模型误差和负载交联耦合干扰对系统的影响,提出了一种基于模糊神经网络运算法则的自适应控制方法,设计了自适应控制器,并在控制系统中加入了模糊神经网络运算法则,最后基于MATLAB软件进行仿真实验,实现了机器人轨迹跟踪的高精度控制。文献[6]针对并联机构存在参数变动和模型误差的情形时,提出一种基于模型的参考PID控制方法,基于Lyapunov函数方法优越的特点,设计了自适应控制器,实现了机构在做复杂运动时仍具有较高的跟踪精度。杨撷泉等[7]针对一种液压并联机器人的杆件结构非对称问题,提出了在输入输出信号中加入具有复合控制的模糊PID控制算法,并结合MATLAB软件,采用仿真实验证明了该方法不仅在很大程度上补偿了并联机器人系统非对称的动力机构对运动系统产生的影响,而且提高了系统的抗干扰能力。
本文针对液压伺服系统存在的参数摄动和复杂外干扰的问题,提出了一种基于动态模糊神经网络的鲁棒复合控制方法,并通过MATLAB仿真实验验证其性能。
1 并联机器人的负载耦合分析
本文研究的6-DOF液压并联机器人的机构简图如图1所示,六条分支杆件共同作用于同一个负载,从而出现了一系列交联耦合干扰对系统轨迹跟踪精度影响的问题。
假设忽略整个机构系统的摩擦力,则装置于分支动杆上液压缸的力平衡方程为:

式中,fi为第i条分支杆件液压缸的实际输出力矩;τi为第i条分支杆件液压缸的液压输出力矩。
依据推导可以得到动平台的动力学方程还可表示为:

其中,F=[FxFyFz],M=[MxMyMz]
J-T可以表示为:

对式(1)、式(2)和式(3)分析可知:

公式(4)可以写为:

其中,Y(s)为六条杆件的长度矩阵,且Y(s)=[y1y2…y6]T;Γ(s)为六条杆件的液压输出力矩矢量矩阵,Γ(s)=[ττ…τ]T。
126
H(s)为交联耦合矩阵。

2 基于动态模糊神经网络的鲁棒复合控制器设计
为了使液压系统具有更好的输出性能,对控制系统进行了四种控制器的设计,PD控制器是为了使整个系统具有更好的鲁棒性能;鲁棒内回路控制器用来消除存在的参数摄动和外部复杂因素干扰;零相位误差跟踪控制器为了实现机构轨迹跟踪的高精度控制;动态模糊神经网络补偿器为了实现对PD控制器的补偿功能,并且为了进一步消除负载交联耦合干扰对系统的影响,具体结构如图2所示。

图2 鲁棒复合控制器框图
2.1 鲁棒内回路控制器的设计
为了消除存在的参数摄动和外部复杂因素干扰问题,对系统进行鲁棒内回路控制器[8]的设计,结构框图如图3所示。其中K(s)代表反馈补偿器;G(s)代表系统模型;Gn(s)代表名义模型。

图3 鲁棒内回路控制器
本文针对控制器K(s)的设计问题,提出了对系统加入一种滤波器Q(s),并加入H∞混合灵敏度的优化方法。
本文选择的滤波器Q(s)为:
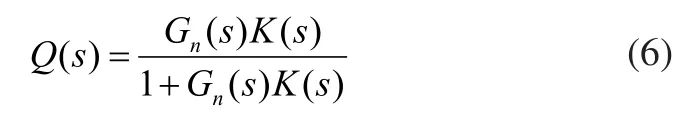

图4 干扰观测器框图
如果将Q(s)替代K(s),则可以用图4来等价的表示图3的结构模型,只要能够使式(6)成立,则控制器就可以转化为干扰观测器的结构,然后基于此干扰观测器的基础上对系统进行分析。
将ur,d,ξ作为输入,则根据叠加原理可以推导出系统的输出为:
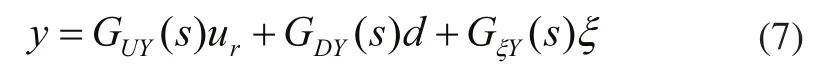
并且有:
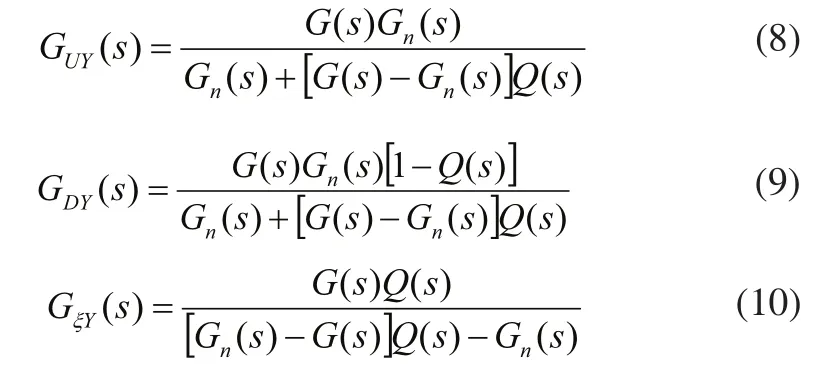
假设Q(s)为理想的滤波器,设Q的频带为fq,当当处在低频段时Q(s)=1,且有:

当处在高频段时f≥fq,Q(s)=0且有:

通过上述分析可知,在对Q(s)优化并处于低频段时Q(s)≈1,针对各种参数摄动和复杂外部干扰具有较强的抑制作用,且提高了系统的鲁棒性。
干扰观测器的传输函数Gol(s),灵敏度函数SQ以及补灵敏度函数TO分别为:

本文基于H∞混合灵敏度[9]的优化方法对Q(s)进行设计。而且求出了最优控制器K(s)。可以将H∞表示为:

其中,W1、W2代表权值系数。
以下将基于H∞理论法设计系统的最优控制器K(s)。
根据对液压伺服系统的分析可以得到其名义模型为:

其中W1、W2取值为:

基于MATLAB环境下的Robust工具箱,并依据式(20)得到了系统的最优鲁棒内回路控制器为:

2.2 位置闭环控制器的设计
本文针对系统采用PD控制,以提高系统的稳定性能,并设置其控制器的关键参数为Kp=5.9,Kd=0.031。
2.3 零相位误差跟踪控制器的设计
本文提出一种零相位误差跟踪控制器用于实现动平台轨迹跟踪的高精度控制[10]。
系统的离散事件传递函数为:

其中,z-d表示模型的延迟导致的滞后,d表示延迟步数。
系统的零点、极点可由如下公式得到:

引入逆系统作为其前馈控制器,则:

对于式(25)所描述的系统,如果输入信号中的d+n值已知,那么控制器可以表示为:

以下对系统的零相位误差跟踪控制器进行设计然后将输入信号设置为正弦函数,并且测量处于不同频率下的相位差,传递函数为:

将Gc(s)离散化可得:

G(z-1)含有一个不稳定点z=9.1410,所以依据原理
cu可以获知ZPETC为:

2.4 动态模糊神经网络补偿器的设计
动态模糊神经网络[11]如图5所示,用xn作为网络的第n个输入,作为第k个节点的净输入。
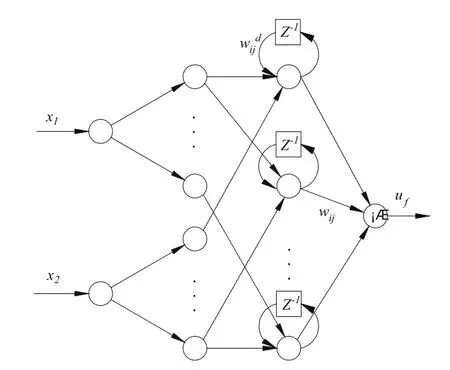
图5 四层动态模糊神经网络结构
第一层:输入层。本文针对输入信号作如下的归一化处理:
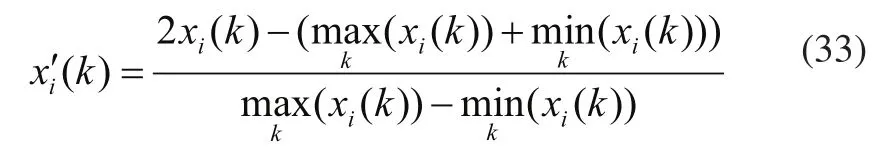
i的最大值。
第二层:隶属函数层。

式中,mij代表第i个输入量的第j个模糊语言变量隶属函数的均值;σij代表第i个输入量的第j个模糊语言变量隶属函数的标准值。
第三层:模糊规则层。

第四层:输出层。主要用于去模糊操作。
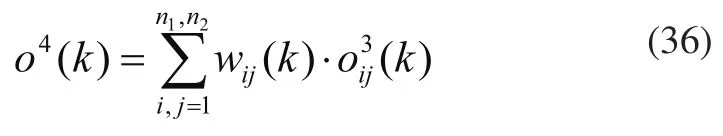
式中,wij为权系数;n1表示x1的模糊变量个数;n2表示x2的模糊变量个数。
将模糊网络的参数用矩阵等形式体现出来,可知输入为:

输出为:

输入隶属函数的向量可表示为:

回归权向量为:
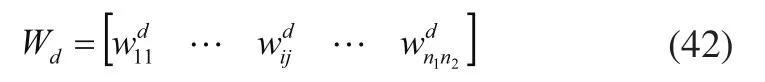
输出权向量为:

根据上述的分析可知,动态模糊神经网络的输出可表示为:
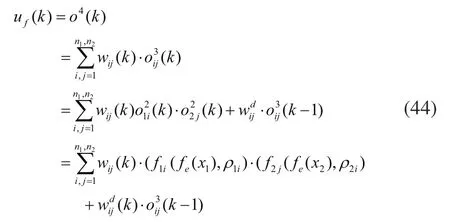
液压系统模型为三阶系统,经简化后的方程为:

可以推出鲁棒复合控制器的输出为:

将式(46)带入式(45)可得:

根据式(47)可知:


定义变量:

由式(48)和式(49)可知:

综上分析,当λ=0时,动态模糊神经网络对外部复杂干扰进行了完全的补偿。
取性能指标函数为:

根据梯度下降法可得神经网络的迭代算法为:

根据式(44)可得:

在对鲁棒复合控制器进行设计时,可以取其输入变量分别为e和uf,它们分别都取五个模糊变量,并且可得e和uf的初始参数为:

经推导可以得到模糊神经网络有25条模糊规则,设规则层与输出层之间的初始参数W为:

当基于动态模糊神经网络补偿器对系统进行控制时,液压系统的模型参数为:

3 仿真实验研究
本文将基于MATLAB软件对6-DOF并联机器人的单通道液压系统展开深入的仿真实验研究。
文章中PD表示闭环控制器,RIC表示鲁棒内回路控制器,ZPETC表示零相位误差跟踪控制器,DFNN表示动态模糊神经网络补偿器。
仿真参数设置如下:杆长幅值0.01m,采用正弦信号,频率为0.5Hz,液压系统单通道受到的干扰力是设置液压无阻尼频率为ωh和液压阻尼比ξh是可以变动的,假设:

当基于PD控制时,得到如图6所示的仿真图形;当加入本文提出的PD+RIC+ZPETC+ZPETC鲁棒复合控制器时,得到如图7所示的仿真图形。
依据图6分析可知,当系统采用PD控制时,轨迹跟踪误差大约为[-0.0005,0.002],反映出严重的不对称性,原因主要是系统负载交联耦合干扰对系统的影响,当基于PD+RIC+ZPETC+ZPETC控制时系统的误差保持在[-0.0002,0.00025],由此可知,鲁棒复合控制器的应用大大的消除了系统参数摄动和外部复杂因素干扰的问题,在很大程度上提高了液压系统的运动性能。

图6 PD控制跟踪曲线

图7 PD+RIC+ZPETC+ZPETC控制跟踪曲线
4 结束语
本文提出的基于动态模糊神经网络的并联机器人鲁棒复合控制方法,解决了并联机器人液压伺服系统存在的参数摄动和外界不确定性因素干扰的问题,文章分别通过PD控制和基于动态模糊神经补偿器的鲁棒复合控制对系统的运动性能进行了仿真分析,结果证明,本文提出的鲁棒复合控制方法在性能上远远优于传统的PD控制,值得推广使用。
[1]成磊,朱龙英,郑帅,等.并联机器人的粒子群优化神经网络自适应控制算法研究[J].制造业自动化,2014,36(6):5-7.
[2]朱大昌,刘运鸿,冯文结.3-RPC型并联机器人模糊PID控制系统研究[J].机械传动,2014,38(002):114-117.
[3]Kim H S,Cho Y M, Lee K.Robust nonlinear task space control for 6 DOF Parallel manipulator[J].Automatica,2005,41(9):1591-1600.
[4]赵东亚,李少远,高峰.六自由度并联机器人分散鲁棒非线性控制[J].控制理论与应用,2008,25(5):867-872.
[5]朱大昌,陈强.基于模糊神经网络运算法则的并联机器人自适应控制研究[J].控制理论与应用,2010,29(1):4-7.
[6]鲁开讲,师俊平,淡卜绸.基于稳定性的并联机构自适应控制[J].农业机械学报,2012,43(1):202-207.
[7]杨撷泉,赵克定,吴盛林.液压六自由度并联机器人控制策略的研究[J].机器人,2004,26(3):263-266.
[8]Bong K, Choi h.Analysis and design or robust motion controllers in the unified frameworks[J].Journal of Dynamic System,Measurement and Control,2002,124(6):313-321.
[9]方强,姚郁.电动负载模拟器扰动观测器系统化设计[J].哈尔滨工业大学学报,2007,39(3):349-353.
[10]Tomizuka M, Zero phase error tracking algorithm for digital control[J].ASME Journal of Dynamic Systems Measurement and Control,1987,109(1):65-68.
[11]Chen Y C,Teng C C.A model reference control structure using a fuzzy neural network[J].Fuzzy Sets and Systems,1995,73(2):291-312.

