机器人系统中交流伺服电机控制研究
庄 丽
(包头职业技术学院,包头 014030)
0 引言
工业机器人是集合了多个学科的高新技术设备,在各个领域应用广泛,最近几十年发展迅速,在当今经济发展中起到至关重要的作用,并且对未来的工业发展起到关键的促进作用。当前工业机器人技术使其自动化程度很高,可灵活应用,同时抗干扰能力强,可以胜任大多数的生产环境,可以一定程度上代替人类的体力和脑力劳动[1]。机器人动作的实现归根结底是伺服电机来实现的,从一定意义上讲,工业机器人的性能取决于伺服驱动控制系统的性能。在工业机器人应用中,对交流伺服系统提出了较高的性能要求,可以归纳为启动速度快,动态性能好,适应频繁启停并且可以最大转矩启动,调速范围要求宽并且在整个调速范围内平滑连续,抗干扰能力强等。交流永磁同步电机能够满足上述的性能要求,已经逐渐成为工业机器人驱动电机的首选[2]。
为了实现更好的电机控制性能,各种伺服控制策略大量出现,各控制策略都有各自的特点。恒压频比控制是控制输出电压和输出频率之比为常数,使电机的磁通量为固定值来控制电机速度,控制实现方法简单、运行稳定。但是该方法不能直接控制转矩,性能较低;矢量控制方法是将电机定子电流矢量经过坐标变换分解为相互正交的交直轴分量,可以等效成直流电机控制,该方法原理较简单,动态性能较好,但也存在计算量大,不能完全解耦的问题;直接转矩控制是采用定子磁场定向的控制方式,对交流电机的电磁转矩进行直接控制,其优点是转矩动态响应快,缺点是在转速较低时转矩脉动大。
本文在对上述控制方法研究的基础上,将矢量控制与模糊控制理论结合实现伺服控制器的参数自整定。自主设计了硬件工作电路,通过专用微控制器软件设计完成具体的算法设计。实现了机器人交流永磁同步电机的快速稳定控制。
1 永磁同步电机矢量控制
永磁同步电机(PMSM)通常定子上有A、B、C三相对称绕组,转子上装有永磁体。定转子相对运动,电磁关系复杂。为简化分析,假设忽略磁路饱和、磁滞及涡流损耗,忽略转子上的阻尼绕组,忽略温度影响,并假设气隙磁场为理想正弦分布。
当永磁同步电动机(PMSM)定子绕组中通三相交流电时,可以得到基于电磁感应定律和基尔霍夫定律的定子电压,定子磁链与转子耦合磁链的方程式[3]。首先约定UA、UB、UC分别为定子绕组相电压;iA、iB、iC分别为定子绕组相电流;ΨA、ΨB、ΨC为定子绕组磁链;ΨrA、ΨrB、ΨrC为各绕组耦合磁链;RS为定子绕组电阻;Ls为定子绕组电感;Ψr为转子磁链幅值。则方程式可以表示为,
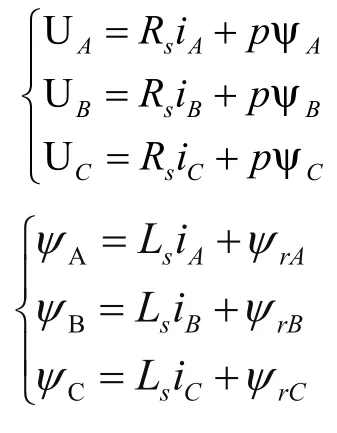

经过CLARK和PARK坐标变换,可以得到两相同步旋转dq坐标系下的方程式[4],
其中电压方程为
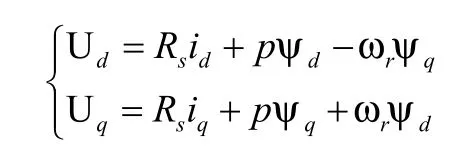
另外,磁链方程可表示为

根据上述坐标系变换后的方程,可以对永磁同步电机的定子电流矢量进行解耦。解耦后的方程可以使用矢量控制的方法进行控制。其中id=0的方法最为简单,在该方法中直轴励磁电流分量为零,根据系统的性能要求来控制交轴分量的幅值和方向就可以实现对永磁同步电机的实时控制[5,6]。交流永磁同步电机的矢量控制结构图如图1所示。
2 控制器参数模糊自整定
从PMSM的矢量控制结构图可以容易看出,交流伺服驱动通常需要电流内环和速度外环的双闭环控制器。这种控制通常采用PID控制器,可以得到较好的控制效果和鲁棒性(robustness)[7]。交流伺服驱动系统具有二阶系统的特征,PID控制器设计时引入微分作用可能使系统抗干扰能力下降,使系统不稳定产生振荡,因此在电流环及速度环设计中舍去微分环节,仅保留比例和积分环节。
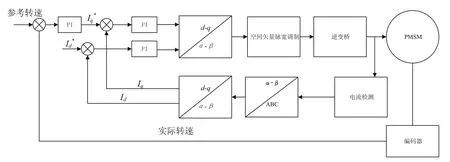
图1 矢量控制结构图
其中比例环节增益kp主要是增加系统的跟踪能力,影响系统的控制精度。当kp增大时,控制系统的响应能力增强,反馈与给定参考值的误差减小,控制精度得到提高。不过比例增益过大时,系统会出现较大的超调量,甚至控制系统出现震荡不能稳定运行。当kp减小时,控制系统的调节速度变慢,使系统的动、静态性能都变差。积分环节增益ki主要是减小稳态系统误差,使系统达到无静差的控制效果。积分增益的特性与比例增益相似,过大会导致系统出现很大的超调,动态性能变差,过小使系统很难去除稳态误差,静态和动态性能都不好。
比例增益Kp和积分增益ki的合理选择会影响伺服控制系统的整体稳定性和响应跟踪能力。比例增益Kp和积分增益ki的设计通常是伺服控制系统的重点也是难点。传统的PID控制器参数设定完成后,在系统运行过程中不可进行改变,当系统参数变化或者有负载突变的情况下,不可改变的控制参数对系统的动态性能有一定的影响。因此,控制参数自整定技术在实际应用中有一定的需求。
基于模糊理论的参数自整定方法在工业控制中得到了一定的应用。模糊理论是模仿人对系统的控制思维来对被控系统各参数变化及负载扰动做出改变,但是单独使用模糊理论还不足以达到精度的高要求[8]。因此我们可以结合经典PI调节器高控制精度的特点,将模糊控制与经典PI控制器有机结合,使PI调节器可以在动态控制过程中调整控制参数得到更好的动态控制效果。图2为模糊参数自整定控制结构。
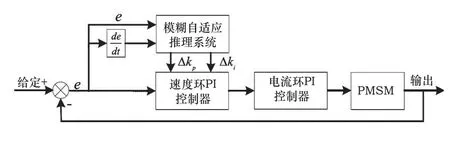
图2 模糊参数自整定控制结构
3 实验验证
为了验证基于模糊理论参数自整定的伺服控制方法的优越性,本文设计了一套实验方案来检验。采用可控智能整流模块及逆变模块的背靠背硬件结构。硬件主要包括三菱1200V等级IPM功率模块,德州仪器F28377D双核微控制器等。交流伺服电机选用Siemens 1FK7高动态型(HD)永磁同步电机。在同样的硬件平台下分别采用模糊参数自整定PI控制和经典PI控制两种方案对PMSM进行控制实验,比较速度表现及转矩表现。
首先观测电机突然加速过程中两种控制方法的速度表现,图3为突然加速到1500r/min的情况。从图中我们可以看到模糊参数自整定PI控制方式在平稳性和稳态误差方面有一定的优势。
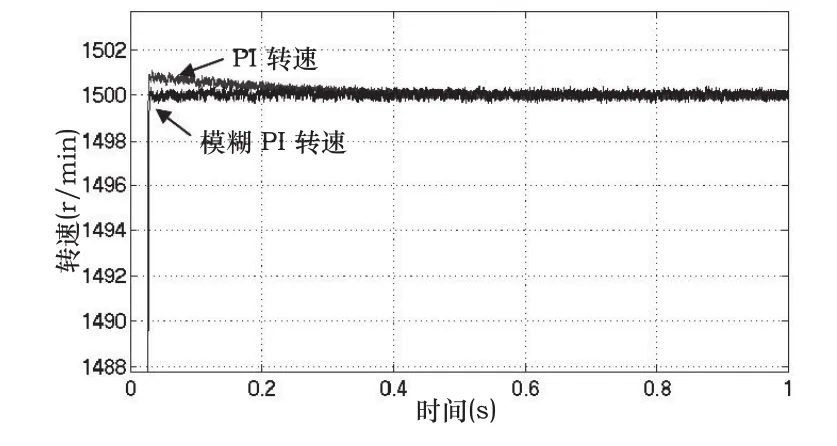
图3 突加转速速度波形
实验在固定转速下突加负载时两种控制方法的转速变化情况,图4给出了突加负载转速扰动的情况。不难看出,模糊参数自整定PI控制方法转速更快的恢复稳态,动态控制效果更优于经典PI控制器方式。
4 结论
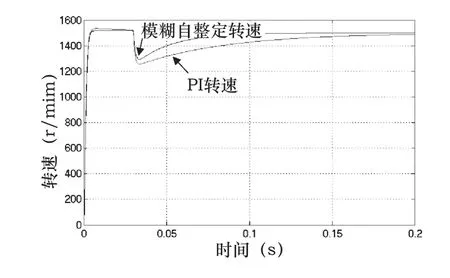
图4 突加负载时速度表现
本文概述了机器人系统中交流伺服电机控制理论及设计方法。分析了经典PID控制器应对机器人交流伺服电机启动速度快,动态性能好,适应频繁启停并且可以最大转矩启动等要求表现出的不足,设计了模糊理论参数自整定与经典PI控制器有机结合的方法,可以有效的改善交流伺服电机的稳态速度稳定性及负载扰动的快速恢复性。通过对比试验验证了本文所涉及方法的有效性。本文所设计的方法不局限于工业机器人交流伺服电机控制,更可以扩展到诸如数控机床等对伺服电机有高性能要求的应用中,具有一定的使用价值,对于推动工业机器人在工业上的应用起到一定的积极作用。
[1]李瑞峰.中国工业机器人产业化发展战略[J].航空制造技术,2010:32-37.
[2]寇宝泉,程树康.交流伺服电机及其控制[M].机械工业出版社,2008.
[3]李崇坚.交通同步电机调速系统[M].科学出版社,2006.
[4]廖晓钟,刘向东.控制系统分析与设计[M].清华大学出版社,2008.
[5]Lin F J, Lin C H.A Permanent-magnet Synchronous Motor Servo Drive Using Self-Constructing Fuzzy network controller[J].IEEE transactions on energy conversion,2004:66-72.
[6]牛洪海,赵荣祥,吴茂刚.基于模糊PI参数自整定的永磁同步电动机矢量控制系统[J].电气应用,2005,24(12):79-82.
[7]黄峰,岳峰,顾军,等.模糊参数自整定PID控制器的设计与仿真研究[J].光学精密工程,2004,12(2):235-239.
[8]孙增圻,邓志东,张再兴.智能控制理论与技术[M].清华大学出版社,2011.

