复合环境试验夹具灵敏度分析及多目标优化设计

李海峰，刘建波，邓谷雨，王东升

（1.中国工程物理研究院 计算机应用研究所，绵阳 621999；2.中国工程物理研究院 总体工程研究所，绵阳 621999）

0 引言

武器产品在使用过程中将遇到振动、加速度、温度、噪声等恶劣环境，为保证使用可靠性，需要通过大量地面环境模拟试验来判断、评估其环境适应能力[1]。当前，受限于技术水平，多数环境试验只针对某单一环境因素进行，但在武器产品贮存、运输和使用过程中常常受到多种环境因素共同作用，并且不同环境因素之间相互影响，如高温与振动两种环境同时作用会相互强化对方的影响。在许多情况下，多环境因素共同作用比其中任何一种单一环境因素对武器产品的影响更严重。随着计算机、自动控制技术的发展和武器产品研制的需求，工程上迫切需要开展复合环境试验研究。

夹具是连接振动台和试件的过渡装置，起着连接或固定试件、传递能量和运动的作用。夹具结构设计是模拟环境试验中一个非常重要的环节，试验安全性、结果可信度与其结构设计、制造及安装、使用水平密切相关。夹具特性对试件响应的影响非常显著，往往关系到试验能否顺利实施、武器产品能否按规定的环境条件经受考核。当夹具发生共振时，输入和输出将不再保持相同的值，并且夹具上各点运动参数也不再保持一致，这将对试验结果产生很大影响[2]。因此，理想的夹具是在试验条件下不破坏、不出现共振，且具有足够的刚度将振动台的能量传递给试件。

由于振动平台环境信息不足并且平台动力学特性设计难度大，目前国内外工作重点仍关注于夹具结构设计，并以实现载荷传递为首要目标[2]。在国内环境试验中，大都采用经验设计结合有限元方法进行夹具设计，基本能满足试验要求，但存在设计周期长、改进后性能提高小等缺点。因此，需要根据实际情况对夹具结构进行优化并改进设计，重点关注夹具结构的质心、强度、刚度、动力及抗振特性、质量及综合性能，最终使夹具满足试验要求，做到设计工作周期短、质量高、效率高、成本低。

本文根据工程实际，从安全角度角度出发，提出了对某振动—加速度复合环境试验夹具结构尺寸进行优化设计的方法。以结构固有振动频率和承载时应力为响应，以尺寸为设计变量，由响应面法[3]得到各响应与设计变量的函数关系，求出其灵敏度。根据目标重构法[4]将各单目标响应耦合，用约束非线性最优化方法[5]，引入约束条件寻优，求得夹具结构响应多目标优化结果。其目的是在满足夹具质量和外形尺寸约束条件下，如何设计在惯性载荷与振动载荷联合作用下动态特性最优的试验夹具。

1 夹具结构

该复合环境试验夹具呈“U”型结构，由底板、立板、侧板、加筋板及试验件（圆柱1与圆柱2组成）组成，其结构对称，如图1所示。夹具结构底板处通过螺栓与振动台连接，立板夹持放置试验件，加筋板固定支撑立板。夹具结构各板件长宽已定，厚度取值可变。

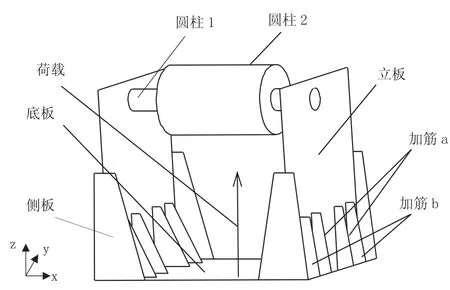
图1 夹具与试件结构示意图

夹具主要承受垂直于底板平面的加速度惯性荷载。其约束条件为设计变量约束和质量约束，设计变量约束需要满足一定的取值范围，质量约束为夹具结构总质量不超过某限定值。

为尽量避免发生共振，需要夹具结构上下振动固有振动频率尽可能高；为满足强度条件在加载时夹具结构不至破坏，需要夹具结构底板、立板最大应力尽可能小，不超过材料屈服应力或最大许用应力。在对该结构进行优化时，首先使单方面的要求得到最大程度的满足，这需要对频率、底板最大应力、立板最大应力分别进行单目标优化分析。实际上，各响应单目标寻优过程中设计变量的变化趋势、变化幅度一般并不一致，甚至存在冲突，即在某单目标优化达到最优时，另一单目标优化并不在最佳状态。为综合考虑各目标的优化效果，使夹具结构总体安全性能达到最优，在进行各单目标优化之后，然后将各单目标响应按某种方式进行耦合，进行多目标优化分析。

2 夹具结构响应数学模型

2.1 响应数学模型

根据夹具结构的设计要求，确定了夹具结构的三个响应：上下振动频率f、底板最大应力Sb、立板最大应力Ss；结构设计变量分别为底板厚度x1、立板厚度x2、加筋厚度x3，其变量响应关系记为。

2.2 响应数据源

建立夹具结构的有限元模型，通过模态分析和静力分析获得不同设计变量取值下结构的频率、应力取值。底板、立板、侧板、加筋板采用四边形壳单元建模，试验件采用六面体实体单元建模。

设变量x1、x2、x3的取值范围，分别为通过对设计变量取值范围线性插值的方法获取工况样本，如将各变量最大增量等分，变量取值如所示，则各变量取值组合共有n3种工况，分别计算此n3种工况获得夹具振动频率和底板、立板最大应力随变量变化的数据源，记为。

2.3 拟合公式

其中，xi为各工况的变量取值，yi为计算所得与变量对应的响应值。显然，Q是以为变量的多元函数，式（3）为多元函数的极值问题。

由多元函数极值必要条件，有：

即：

即为最小二乘拟合问题的法方程组。

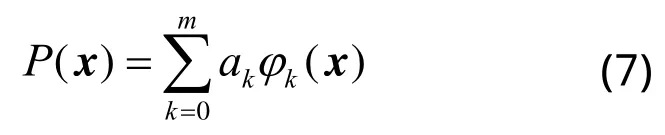
P(x)为所求的最小二乘拟合，即式（1）中的(x)。

根据以上思路与方法，可以得到夹具结构上下振动频率、底板与立板最大应力关于变量x1、x2、x3的完整的拟合公式如式（8）～式（11）所示。

3 夹具结构灵敏度方程的建立与求解

夹具结构灵敏度分析是研究夹具结构的三个响应（上下振动频率f、底板最大应力S1、立板最大应力S2）对三个设计变量（底板厚度x1、立板厚度x2、加筋厚度x3）变化的敏感程度，灵敏度的高低反应了夹具结构在参数改变时对设计函数的影响，可用来评价夹具结构优化的可行性，识别夹具结构的临界值、极限值或破坏值，确定夹具结构最优解的搜索方向。

约束条件下，令响应的灵敏度函数均等于零，获得响应的灵敏度方程组，该方程组的解的意义为：夹具结构在满足设计约束时，响应取得极值或驻值。为将约束条件引入响应的灵敏度方程组，需采用拉格朗日乘子法[7]。

已知夹具结构的约束条件为质量约束，即其质量不大于某定值M，可表示为式（12）的形式。

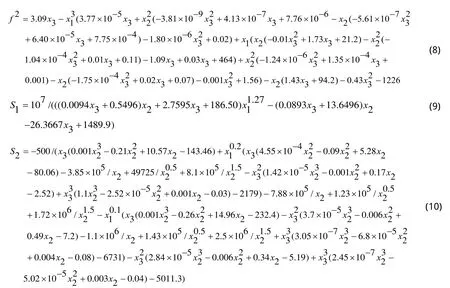
的函数。

引入松弛变量x4，将夹具结构的质量不等式约束式（12）转化为等式约束：

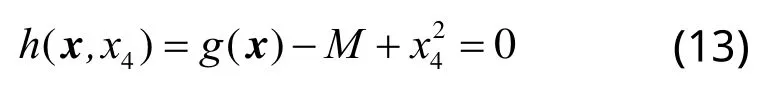
该方程组为非线性方程组，可用牛顿迭代法进行求解，其迭代公式为：

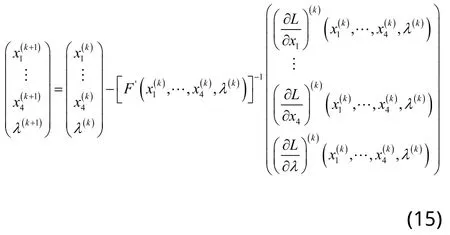
牛顿迭代法的收敛结果即为方程组（14）的数值解，排除驻值，将响应的极值与下面单目标优化结果做对比，可验证响应单目标优化的精确性。

4 夹具结构优化设计

4.1 夹具结构单目标优化

本文单目标优化的目标分别是：上下振动固有频率最大；底板最大应力最小；立板最大应力最小。当将该固有频率的负值最小作为优化目标时，其单目标优化的数学模型可统一表示为：

其中，响应y可表示夹具结构固有频率、底板最大应力和立板最大应力。

采用增广拉格朗日乘子法，引入松弛变量将式（17）转化为等式约束问题：

引入罚因子T≥0和拉格朗日乘子λ，以为λ的k次迭代，定义增广拉格朗日函数：

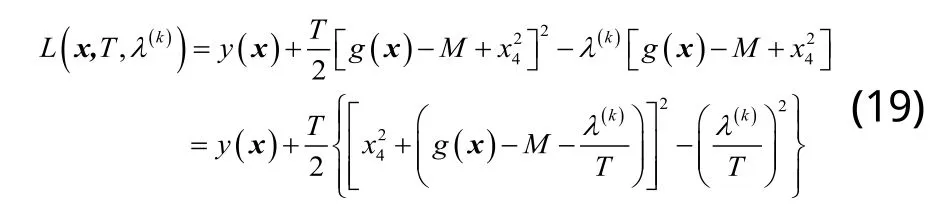
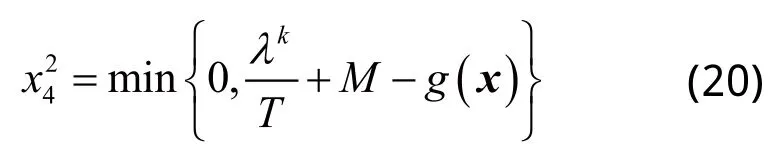
即：

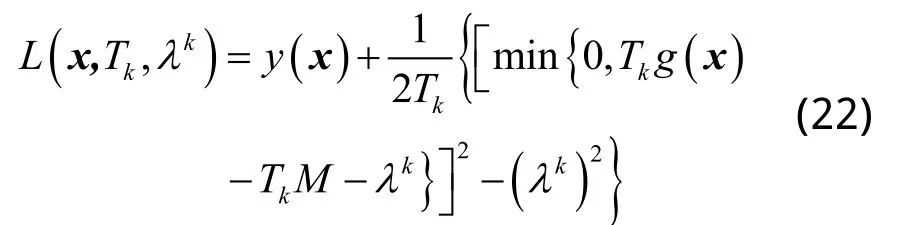
设允许误差ε＞0，当有时，迭代终止，为式（22）的最优解，即式（17）的最优解。其计算迭代过程可通过MATLAB编程实现，优化结果如表4所示。

4.2 夹具结构多目标优化

该夹具结构优化具有两个特点：各设计变量为连续变化的实数；各单目标优化的层次相同且优化顺序没有先后之分。结合多目标优化各方法的特点，本文采用重构目标法[4]中的理想点法。

理想点法的理论基础为：在可行域中，绝对最优点一般是不存在的，但是对于分目标函数却容易找到其各自的最优解，如果使各分目标函数尽可能接近于各自的最优解，就可以求出较好的优化结果。

理想点法构造的单目标函数为：

其中，iα表示权重，反映了各单目标函数在整个多目标优化问题中的重要程度。

据此，本夹具结构优化模型中，其多目标优化方程将转化为如下单目标函数：

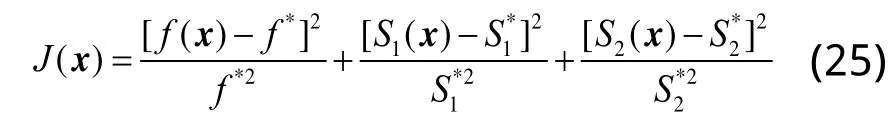
式中：x为设计变量组成的向量；f为拟合所得频率公式；S1为拟合所得底板最大应力公式；S2为拟合所得立板最大应力公式分别为对应的单目标优化结果数值（如表4所示）。

夹具结构的多目标优化问题就转化为求该目标函数取最小值的问题，可用单目标优化的方法来求解。

5 优化算例

形如图1所示的夹具结构，其各板尺寸如表1所示，材料参数如下：密度ρ为2.80x10-9t/mm3、弹性模量E为70000MPa、泊松比μ为0.33、材料屈服极限sσ为220MPa。圆柱尺寸如表2所示，总质量为1.3t，关于X—Z面前后对称，关于Y—Z面左右对称，其中心轴与x轴平行，在Z向的垂直高度为855mm。

表1 夹具结构底板、立板和加筋尺寸

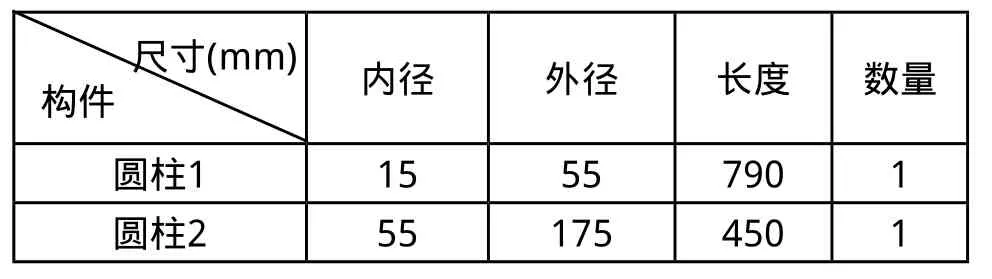
表2 圆柱1、2尺寸

设计变量x1、x2、x3的初始数值为50、50、30mm，其取值范围限定为[30,90]、[30,90]、[10,50]。采用本文方法进行多目标优化，得到各个设计变量取值如表3所示。初值计算结果、多目标优化结束时各响应取值、各响应单目标优化结果及各响应灵敏度方程组的零解对应的响应极值如表4所示。同时，本文给出各响应的Nastran单目标优化结果做为参考。

表3 夹具结构多目标优化结果

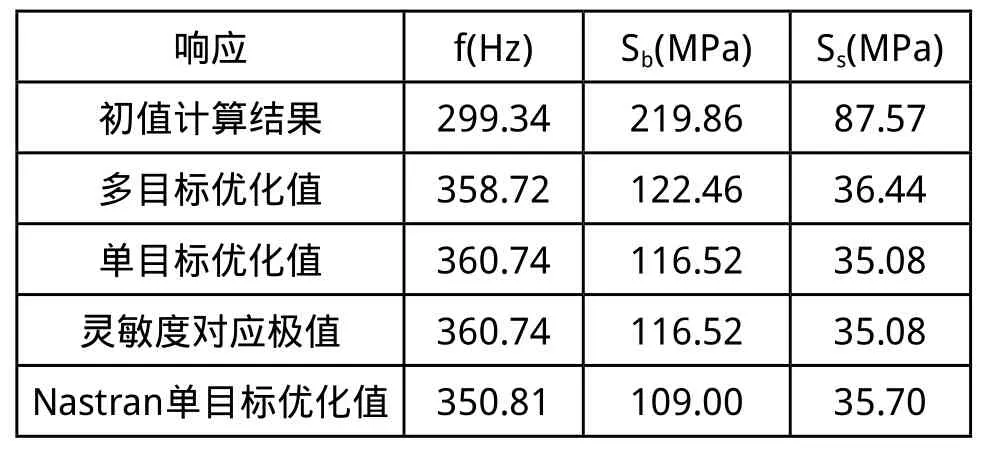
表4 夹具结构单、多目标优化结果比较

从表3、表4可看出，各响应的灵敏度方程组零解对应的极值与单目标优化值完全吻合，与Nastran单目标优化值十分接近，说明本文方法具有可行性和较高的精确度；多目标优化目标函数值与单目标优化值相当接近，最大相对误差5.10%，说明取得较好的优化结果。

6 结论

1）本文研究了某振动-加速度复合环境试验夹具结构优化设计，提出了一种该类夹具结构的单目标和多目标优化的理论方法。

2）以承载时夹具结构上下振动固有频率和关注部位最大应力为响应，提出了用响应面法建立夹具结构的三个响应与设计变量间的函数关系，建立了响应灵敏度的计算公式，对其灵敏度方程组及其解法进行了研究。

3）给出了实现和验证响应单目标优化的方法，利用多维有约束非线性优化法理论实现单目标优化，采用拉格朗日函数法求解响应灵敏度方程组的方法验证单目标优化结果。

4）基于目标重构法将各单目标响应耦合，建立了多目标优化的目标函数，将夹具结构的多目标优化问题转化为求该目标函数最小值的问题，并进行求解。算例结果表明，该多目标优化目标函数兼顾了各单目标优化的影响，具有良好的优化效果，本文提出的优化设计方法是合理、可行、有效的。

[1]邓志刚.基于计算智能的振动—离心复合试验夹具优化设计[D].成都:四川大学,2006,1-3.

[2]王东升,任万发,刘青林,等.振动试验夹具共振频率设计要求研究[J].航天器环境工程,2014,31(1):37-41.

[3]钟毅芳,陈柏鸿,王周宏.多学科综合优化设计原理与方法[M].武汉:华中科技大学出版社,2006.

[4]李春明.优化方法[M].南京:东南大学出版社,2009.

[5]宋巨龙,王香柯,冯晓慧.最优化方法[M].西安:西安电子科技大学,2012.

[6]陈泽,占海明.详解Matlab在科学计算中的应用[M].北京:电子工业出版社,2011.

[7]赫孝良,葛照强.最优化与最优控制[M].西安:西安交通大学出版社,2009.