基于改进多元非线性算法的水泥电耗预测建模
赵 辉,张 宁,蔡万通,王红君,岳有军
(1.天津市复杂系统控制理论及应用重点实验室,西青 300384;2.天津理工大学 自动化学院,西青 300384;3.华北电力大学 电气与电子工程学院,北京 102206)
0 引言
为了降低水泥企业的生产成本并提高经济效益,节能降耗至关重要。如今,在基础自动化设备齐全、工艺改造已基本成型的条件下,水泥企业进一步节能降耗的突破口便在于生产过程中的先进能源管理方面[1]。其中,对电耗量的预测是制定水泥企业能源规划的重要组成部分:通过电耗预测可以使工作人员根据原料供应和生产计划,按照预测限电购电、合理制定与电厂协议的最大需量,从而避免供电不足或过剩的情况。因此,建立一个完善的水泥电耗预测模型成为目前亟待解决的问题。
水泥生产是由众多工序有机结合的一个整体,其能耗预测模型的特点是变量多、关系复杂。针对水泥企业各种工序和大量实际应用的结果,国内外专家学者提出了多种能耗预测方法:文献[2]用线性回归模型预测电力消耗,然而模型的精度有待提高;M.Ali Azadeh等在文献[3]中阐述了一种基于多目标的人工神经网络方法,并将其应用于伊朗高耗能工业部门的年消费电量的神经网络预测,但是该模型的计算量大,收敛速度慢,且很容易陷入局部极值,使训练失败;文献[4]通过结合小波变换和人工神经网络,预测钢铁企业电力负荷趋势,然而该算法较为复杂,且不确定何种小波基较为合适,需要大量实验仿真验证。
总的来说,国外的能耗分析预测研究已较为成熟,但目前建立的模型普遍具有运算量大、收敛时间长、模型复杂等缺点,并不适用于我国水泥企业的能耗预测管理情况;而国内的相关研究主要针对于钢铁行业,水泥行业由于其生产工艺的特殊性,建立的钢铁生产电耗模型又不能直接用于水泥生产上。因此,应综合考虑预测精度、计算复杂度、模型简洁度,以及结合水泥生产的自身参数特点,建立一套适用于我国水泥企业的电耗预测模型。本文在提出水泥生产电耗影响因素的基础上,运用主成分分析法得到了主要影响因素,并运用改进的多元非线性数学模型得到了水泥电耗预测模型,在降低模型复杂度的同时也提高了预测精度。
1 水泥生产电耗的影响因素
为了对水泥生产电耗进行有效预测,应深入分析影响各环节电耗的影响因素,并以此作为变量构建水泥电耗的预测模型。
据统计,在典型水泥厂中的电能消耗情况大致为:采石、破碎为5%;生料粉磨为24%;给料均化为6%;熟料烧成与冷却为22%;水泥粉磨为38%;包装、装载出厂为5%[5]。因此,根据水泥生产电耗的分布可以确定,水泥生产过程中主要的电耗影响因素(x1,x2,…,x11)分别为:生料粉磨细度,生料水分,石灰石硬度,均化效果,燃料筛余量(煤粉细度),回转窑升温速率,熟料冷却速度,煅烧温度,磨机转速,水泥细度和助磨剂掺加量。可见,水泥生产电耗的影响因素众多,且存在明显的相关性[6]。因此,如果可以从以上11个影响因素中提取出主要的影响因素,并用于水泥生产电耗预测模型中,就能减少计算量,提高计算速度和精度。
2 主成分分析法及多元非线性拟合的原理分析
2.1 主成分分析法
主成分分析法(PCA)是利用降维的思想将多个变量转变为少数几个综合变量(主成分),其中每个主成分都是由原始变量线性组成的且互不相关。这些主成分所含的信息能反应出原始变量的大部分信息,且互不重复。在数学变换时保证变量总方差不变,同时新综合变量则按照方差由大到小的顺序排列,即第一主成分、第二主成分[7]……以上思想也可以用数学模型表示为:假设分析n个样本涉及p个变量x1,x2,…,xp的问题,可得n×p阶的原始数据矩阵:
鉴于实际问题中涉及到各个指标变量的不同量纲和数量级的差异,为了避免这种不良影响,人们通常会先将原始数据进行标准化处理,得到无量纲矩阵再由主成分分析法得出新综合向量:
其中zp是与均不相关的的所有线性组合中方差最大的。
由大量算例验证[8]可知,经PCA分析后大多数样品的电耗预测绝对误差相比主成分回归前更小,预测精度有了明显的提高。即这种算法可以在保证模型有效的前提下,使复杂问题简化,减少运算量。此外,经PCA预处理过的新综合变量之间互不相关,相当于将原始变量进行解耦处理,方便下一步分析每个自变量对因变量的影响关系,分别进行非线性拟合建模。
2.2 现有的多元非线性建模原理及不足
在工业能耗预测中,常用多元回归模型反映预测量与各因素之间的依赖关系,其中线性回归分析有着广泛应用。但客观数据之间并不一定呈线性关系,有时非线性回归模型更为合适。根据自变量的个数,非线性回归又分为一元非线性回归和多元非线性回归。其中一元非线性回归(曲线回归)模型主要有倒幂函数双曲线函数幂函数倒指数函数对数函数S型函数等。
现有的多元非线性回归预测建模原理[9]为:首先分别建立y与各变量的最佳一元非线性回归模型,可以由多组数据画出散点图,由图像判断拟选取的模型;也可采用探索性的方法,在SPSS统计软件中选中所有曲线模型,综合比较多个参数(如比较相关系数R,判定系数R2,标准误差SE等)从中选择最合适的一元回归模型最后将y对进行多元线性回归,即建立了y对所有变量的多元非线性回归模型,最后计算其拟合程度,只要误差通过检验即可用于预测。
然而,上述预测方法存在一定的不足:求解每个自变量对因变量的影响关系时、建立的一元非线性回归模型均是基于某种单一非线性初等模型建立的,而实际上,其函数复杂关系可能是多种非线性初等模型的组合。这与实际情况可能有一定差距,即此模型精度仍需进一步提高。
2.3 改进的多元非线性建模原理及优势
2.3.1 思路概述
如上节所述,分析每个主成分变量与水泥综合电耗的影响关系时、其函数复杂关系可能是多种非线性初等模型的组合。即每个主成分变量Xp的总表达式应为:
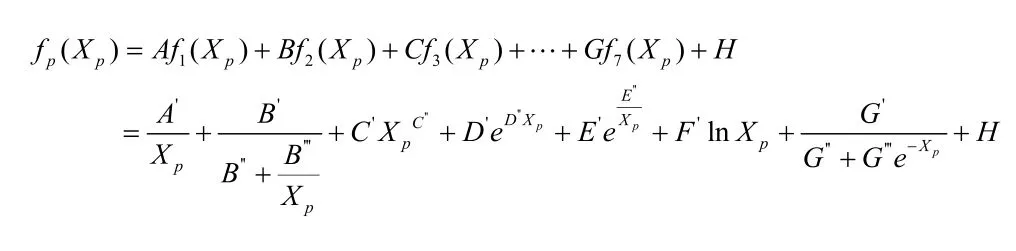
上述模型在编程求解时,虽然理论上可以达到高精度要求,但关于初值和步长很难确定,且计算量大、过程繁琐,得到的模型过于复杂。
由泰勒公式、麦克劳林级数等函数逼近理论[10]可知,初等函数可以通过幂级数展开,转换为多项式加和的形式,且误差也足够小,即函数的幂级数展开问题在数学上是可行的。因此,上文中建立的由多个初等函数线性组合而成的复杂模型即可简化为的形式,再由最小二乘法多项式曲线拟合原理求解未知系数。
2.3.2 原理及步骤
最小二乘法多项式曲线拟合[11]并不要求这条曲线精确地经过所有点,而是曲线的近似曲线给定数据点,求近似曲线,并且使得近似曲线与的偏差最小。近似曲线在点iP处的偏差而以为原则选取拟合曲线的方法,即为最小二乘法。具体步骤如下:
1)设拟合多项式为:

2)各点到这条曲线的距离之和,即偏差平方和为:

3)为了求得符合条件的系数,即求极小值需要使ak的偏导数=0,因而化简整理得矩阵形式的方程组:
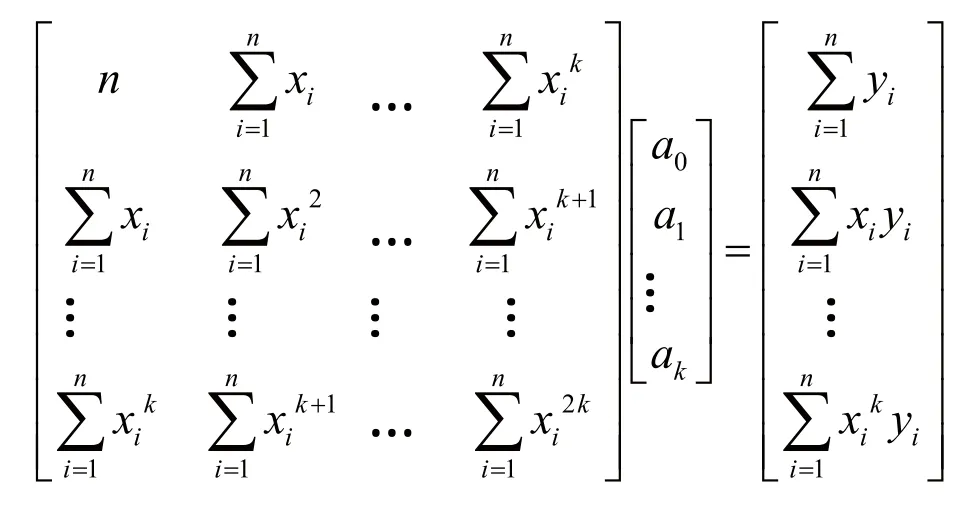
2.3.3 模型优势
本文提出的基于改进多元非线性算法的电耗预测模型在对每个主成分进行一元非线性回归时,通过对各种初等函数幂级数展开,既考虑了初等函数的复杂组合,又使最后的结果形式统一。在保证高精度要求的同时,又能使复杂模型形式简洁,求解方便。
3 算例分析
本文以平邑中联水泥厂为例,分析实际生产运行数据,并在主成分分析的基础上,搭建基于改进的多元非线性算法的水泥电耗预测模型。
3.1 基于PCA的数据处理
根据前文分析的与水泥电耗相关的十余种影响因素,于平邑中联水泥厂的DCS系统数据库中选定拟采用的典型原始数据。值得注意的是,要选取采集时间最近的数据,且排除各种生产故障工况。经PCA处理得到四个正交不相关的新综合变量X1、X2、X3、X4的函数表达式为:

3.2 现有的多元非线性水泥电耗预测建模
经PCA处理后得到4个新综合变量,通过一元曲线回归分别估算出水泥电耗与各因素的回归公式,根据各统计检验量列出最优曲线回归模型。以X1为例,输出结果统计如表1所示。

表1 第一主成分的各回归模型统计数据
比较几个曲线回归模型的判定系数R2:其中对数曲线方程中R2=0.986最大,因此变量X1的最佳一元曲线模型为:
f1同理可得变量X2、X3、X4的一元曲线回归模型:

于是可建立回归模型:

用已建立的三个一元非线性函数作为输入变量,线性回归确定各自系数,可得结果:
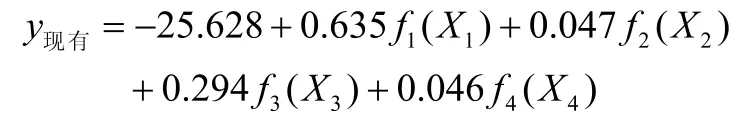
3.3 改进的多元非线性水泥电耗预测建模
以第一主成分X1与水泥电耗关系的求解为例,利用MATLAB进行非线性回归拟合。由拟合曲线及所得系数结果发现:k从0逐渐增大时,一定范围内,k的增大可以减小模型误差、提高精确度;但k值也不能过高,当k>5,大部分系数几乎为0,即便是与自变量的幂数相乘也很小,而当k>10时拟合的曲线出现畸变。经多次尝试得到k取3时拟合的曲线最贴近实际生产运行曲线。可得拟合曲线表达式:
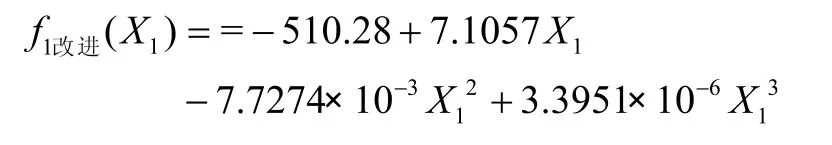
同理可得第二、第三主成分分别与y的关系式为:

剩余步骤同理:建立回归模型:

确定系数,得到改进后的数据拟合计算公式:

最后分别比较y改进、y现有与实际数据的拟合效果,如图1、图2所示。

图1 预测电耗与实际电耗的拟合效果对比图

图2 预测模型的相对误差对比图
由图1、图2可以明显看出,改进模型与实际数据的相对误差更小,即改进的多元非线性预测模型的拟合效果更好。
4 结论
本文在确定水泥生产电耗影响因素的基础上,运用PCA对原始数据进行预处理,得到了四个影响水泥生产电耗的关键因素,并在此基础上提出了基于改进多元非线性算法的电耗预测模型,有效预测了水泥生产中的电耗量。以平邑中联水泥厂为例验证了此模型的正确性,并得到结论:经PCA处理后确定的水泥生产电耗影响关键因素,能有效表征和替代原始的十一个影响因素,降低了基于原始数据建立的回归预测模型的复杂度;同时,改进的多元非线性拟合模型能有效提高预测精度,使电耗预测值与实际值有较高的吻合度,对于水泥厂的电耗预测管理具有重要的参考意义。
[1]许文梦.基于MES的水泥企业能效分析研究[D].山东:济南大学,2012.
[2]苗文静.模糊划分线性回归模型在电力负荷预测中的应用[J].水电能源科学,2013,30(3):188-190.
[3]M.Ali Azadeh, Sara Sohrabkhani.Annual Electricity Consumption Forecasting with Neural Network in High Energy Consuming Industrial Sectors of Iran[J].Industrial Technology, 2006, 2166-2171.
[4]张家云,李新胜,等.遗传小波神经网络在钢铁企业能耗预测中的应用[J].冶金自动化,2009(1):845-847.
[5]徐振宁,潘朝平,等.新型干法水泥厂电耗评述[J].水泥工程,2008(4):2-11.
[6]刘仁德.过程质量对水泥生产电耗的影响与控制[J].四川水泥,2013(4):102-110.
[7]黄传坤,王远清.主成分分析方法的应用研究[J].现代商贸工业.2011,23(17).
[8]黄玉龙,吴悦,陈创.热轧吨钢电耗预测模型建立及应用[J].节能技术,2012,5(30):286-289.
[9]王蕊,董祥旻,何卫苹.一种多元非线性回归模型的建立方法及其应用[J].中国考试,2010,11.
[10]朱晓东,鲁铁定,陈西江.正交多项式曲线拟合[J].东华理工大学学报(自然科学版),2010,12(33):398-401.
[11]徐亦唐.基于最小二乘法的曲线拟合及其在Matlab中的应用[J].电子世界,2013,5:102-103.

