基于机器视觉检测的摄像机快速标定与误差分析

丁婷婷，方 舟，刘 波，张君安

（西安工业大学 机电工程学院，西安 710021）

0 引言

畸变不可避免的存在于通过图像采集设备获取的图像中，如果不对其进行矫正，将会直接影响后续处理的准确性和效率。为了进行矫正，先进行摄像机标定。摄像机标定是确定摄像机参数的一个过程[1]，其在三维重建、视觉监控、视觉伺服等领域均有广泛的应用前景，因此具有重要的理论、实际研究价值。

摄像机标定有传统标定和自标定。就目前的研究来看，比较常用的还是传统标定。在工业视觉中，用径向畸变已经足够描述非线性畸变，若引入过多的高阶畸变参数，不仅不能提高标定精度，反而会引起解的不稳定[2]。本文是在Tsai两步标定法的基础上建立的，采用考虑径向畸变的摄像机模型，标定过程中避免了繁琐的非线性优化，并进行逆向求解，得标定块上相对应的空间点的坐标，从而更准确地计算标定误差。

1 畸变矫正的数学模型

工业视觉中，实际成像与理想的针孔成像之间存在光学畸变误差。因此需要在理想的摄像机模型中引入畸变模型。在满足精度要求的前提下，一般情况下只考虑径向畸变模型，引入过多的畸变模型反而会影响计算精度。为了准确快速的完成标定，本文采用了将能精确反映成像过程的带有透镜径向一阶畸变模型引入小孔摄像机模型中[3]，如图1所示。

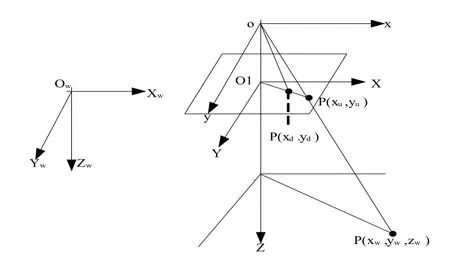
图1 考虑镜头径向畸变的摄像机模型

在模型中涉及4个坐标系，并取目标点为P。则其在各个坐标系下的坐标表示如下：（xw,yw,zw）是世界坐标系(owxwywzw）下物体点P的三维坐标。(xc,yc,zc)是点P在摄像机坐标系(ocxcyczc)中的三维坐标。(xu,yu)是理想摄像机模型下P点在摄像机成像平面坐标系(OXY)中的表示，(xd,yd)为P点的实际图像坐标。(u,v)为P点在计算机图像坐标系(OUV)，以像素为单位。(u0,v0)计算机图像(帧存)中心坐标。dx、dy分别表示每一个像素在x轴y轴的物理尺寸，f为有效焦距。则点P在计算机图像坐标系与世界坐标系中存在如下关系式：

上式中的内外参数可通过摄像机标定方法获得，因此如果已知某空间点的世界坐标，就可以求出该点的计算机图像坐标；已知目标点的计算机图像坐标和某些约束条件，就可以求出其对应的空间坐标。

2 摄像机标定的参数求解

本文是根据上述畸变模型（如图1所示）进行标定算法设计的，需要求解旋转矩阵R、平移矩阵t、有效焦距f和畸变系数k。具体求解流程如下：

1）求解旋转矩阵 R，平移向量 t中的Tx,Ty分量[4]：

根据摄像机坐标系（xc,yc,zc）到世界坐标系（xw,yw,zw）的转换关系，再结合RAC(径向平行约束）和ZW=0，从而计算Ty的值，然后据R的正交性，求得R中各参数及Tx的值。

2）不考虑畸变时，求解有效焦距f、t的分量Tz估计值。

代入n组特征点，从而求出f、Tz的估计值。

3）考虑畸变时，求f、Tz的优化值和畸变系数k（zw=0）。

畸变模型为：

设：

将式（3）、式（4）带入式（2），并代入n组特征点坐标值，用最小二乘法求解超定线性方程即可求得f、kf、Tz，进而求得f、k、Tz。

3 特征点成像误差计算模型

空间中某点P在世界坐标系下与摄像机坐标系下的齐次坐标存在如式（5）所示的关系。

将已知的计算机图像坐标点代入式（6）进行计算，可求得xwi,ywi。在上述逆向求解过程中，由于以上推导是基于透视变换法中的线性针孔成像模型，未考虑畸变。为了计算精确，在式（6）u、v中引入畸变模型（3）得到u`、v`，其中zw=0,利用特征点坐标及其标定求得的参数可求得x`wi、y`wi，从而计算误差。

4 畸变矫正实验与数据分析

为了验证算法的有效性和可行性，本文用HALCON图像处理软件平台进行模拟实验。本实验选用的是平面标定块（如图2所示），拍摄得到的图像如图3所示。相机分辨率为dx=0.01538mm/Pixel，dy=0.01538mm/Pixel，采用的标定模板为6×6个半径为0.4mm的圆。其中u0=184.5（Pixel）、v0=175（Pixel）。

图2 平面标定块

图3 拍摄的标定块图像

1）求标定参数

根据本实验所选的标定块，可以得到标定块上特征点（圆心）的世界坐标（xwi、ywi）单位为mm和相应的图像坐标（ui、vi）单位为像素Pixel，如表1所示（本文取图2中前四列右边的16个圆的圆心坐标作为测试点）。

表2 参数标定结果 (mm)

表3 新特征点与原特征点对比表 (mm)

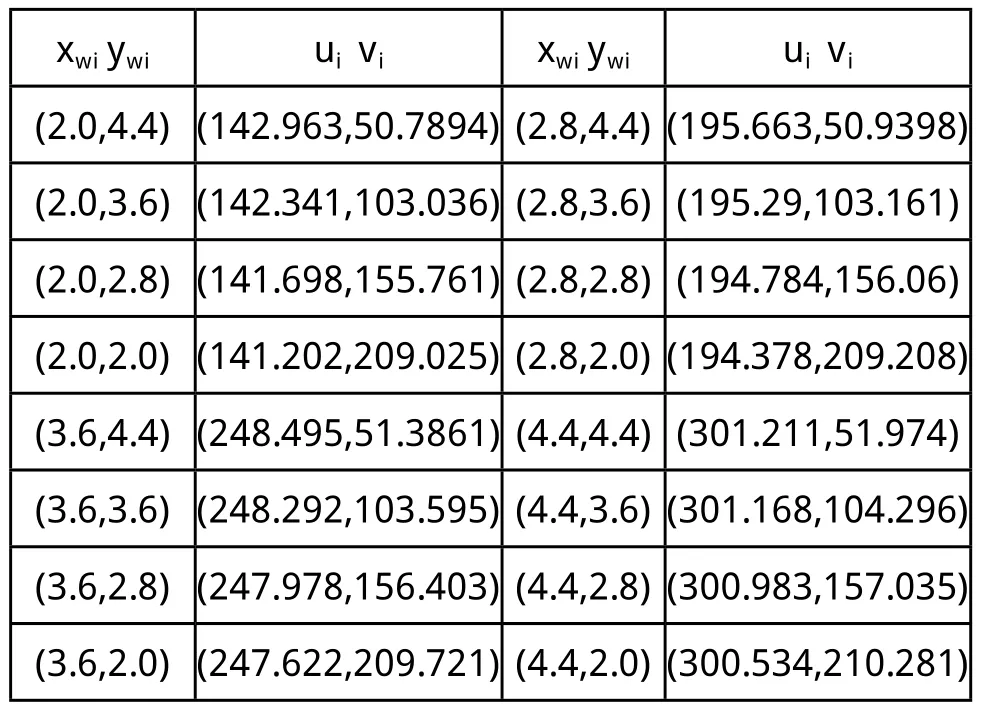
表1 平面标定块的特征点的世界坐标和图像坐标（Zw=0)

据表1中的数据，运用本文的标定算法得参数结果如表2所示。

2）求特征点成像误差

据表2所求得参数及本文的逆向求解算法得到相应的新世界坐标，其中zw=0，特征点的新世界坐标（x`wi、y`wi）和原世界坐标（xwi、ywi）如表3所示。

误差的计算可采用空间世界坐标的绝对误差和相对误差来表示。经计算得绝对误差Ew=0.01449mm，相对误差为ew=4.26‰。

5 结论

在该算法中误差的来源主要有[5]：1)标定板的不平度引入的误差。2)CCD相机与光学成像产生的误差。CCD相机光敏面上的中心距限制了测量的分辨率。

本文采用带有径向畸变的摄像机模型，逆向求特征点，再与原特征点进行数据比较，精确地计算出标定误差。实验验证该算法相对误差达4.26‰，可以快速、准确的完成标定，并且准确计算误差，提高了算法的精度。同时该算法还可以应用在其他有图像畸变的场合进行镜头误差评定，即判断畸变矫正的必要性，如果通过本文算法得到畸变误差足够小，则可略去矫正环节，进而提高了整个计算的效率和准确度，在机器视觉领域具有较强的实用性。

[1]徐杰.机器视觉中摄像机标定Tsai两步法的分析与改进[J].北京科技大学学报,2010,32(4):45-48.

[2]赵宣铭.一种基于Tsai法的摄像机改进标定法[J].西安工程大学学报,2011,25(4):560-564.

[3]李君兰,张大卫,王以忠,等.面向封装的显微视觉定位系统[J].光学精密工程,2010,18(4):965-967.

[4]王建华,冯帆,梁伟,等.基于matlab的摄像机标定系统的设计与实现[J].计算机与数字工程.2012,269(3),97-99.

[5]张海,付伟,高荣杰.机器视觉测量中相机两步标定法的改进[J].华东交通大学学报.2012,46(3):77-80.