云模型在GNSS高程拟合中的应用

张欣杰,栾元重,朱纯强

(山东科技大学,山东 青岛 266510)

云模型在GNSS高程拟合中的应用

张欣杰,栾元重,朱纯强

(山东科技大学,山东 青岛 266510)

针对曲线拟合方法求局部区域高程异常值具有局限性的问题,提出了一种基于云模型的方法对高程异常值进行分析处理。本文按照控制点的位置分组进行曲线拟合,对高程异常值进行定性定量分析形成云形图,直观表现出高程异常值的特性。结果表明新方法能使高程异常值精度提高,验证了GNSS控制高程的可靠性。

GNSS高程拟合;云形图;云模型;高程异常

0 引言

确定大地水准面的方法可归纳为:几何方法、重力学方法及几何与重力联合的方法[1]。这些方法需要大量重力、天文大地观测资料,在我国该方面资料匮乏,一般无法应用于工程测量中。所以在局部小范围内,通常运用全球卫星导航系统(global navigation satellite system,GNSS)高程拟合来计算高程异常[2],例如GNSS测高精度在5～10km的距离上已达到三等水准测量的精度[3]。GNSS高程拟合的方法有很多,主要方法有多项式曲面拟合,多面函数拟合法,曲面样条拟合法,非参数回归曲面法、高程异常变化梯度法、Sheppard曲面拟合法、移动曲面法、加权平均法等[4]。基本原理是根据测区实测数据或者已知点的平面坐标x、y和高程异常值ζ,用数值拟合的方法拟合出测区似大地水准面,再内插或外推出待定点的高程异常值,从而求出待定点的正常高[5]。本文主要研究当数据较多时,用某一种方法进行拟合,选用不同的数据会产生不同的拟合曲线,对内插或外推结果的精度产生不同的影响。使用云模型可以有效的对实验结果进行定性和定量分析,使高程异常值更为准确,精度更高。

1 云模型的原理

云模型是一门较为新型的方法,属于不确定性人工智能的范畴,主要是用于定性与定量之间的互相转换。“云”或者“云滴”(cloud)是云模型的基本单元[6]。设U是一个用精确数值表示的定量论域,C是U上的定性概念,若定量值x∈U,且x是定性概念C在论域U上的一次随机实现,x 对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数,则数据元组(x,μ(x))称为云滴[7],论域U中的全部元素xi(i=1,2…n)与其对C的确定度μ(xi)即n个数据元组(xi,μ(xi))构成具有n个云滴的云模型,x称为云滴定量数据,μ(x)称为云滴的确定度,云滴的定量数据x在论域上的分布称为云分布,并记为:X～C(x|Ex,En,He)[8]。

云模型用三个数据来表示特征:

1)期望Ex(expected value):云滴在论域空间的分布期望,是概念在论域中空间的中心值,是最能够代表定性概念的点。

2)熵En(entropy):它是定性概念不确定性程度的度量,由离群程度和模糊程度共同决定,反映了代表这个定性概念的云滴的离散程度;同时, En又体现了定性概念亦此亦彼性的域度,反映了论域空间可被定性概念接受的云滴的取值范围,是对定性概念[9]。

3)超熵He(hyper entropy):用来度量熵的不确定性,亦即熵的熵,它的大小间接反映了云的厚度。

云有两种发生器(Membership Clouds Generator),正向云发生器和逆向云发生器,分别用来生成足够的云滴和计算云滴的云数字特征(Ex,En, He),首先我们介绍正向云发生器的触发机制[6]:

1)根据云的数字特征生成En为期望,以He2为方差的正态随机数En′。

2)计算期望值Ex,以En′2为方差的正态随机数x,x就是论域空间U的一个云滴。

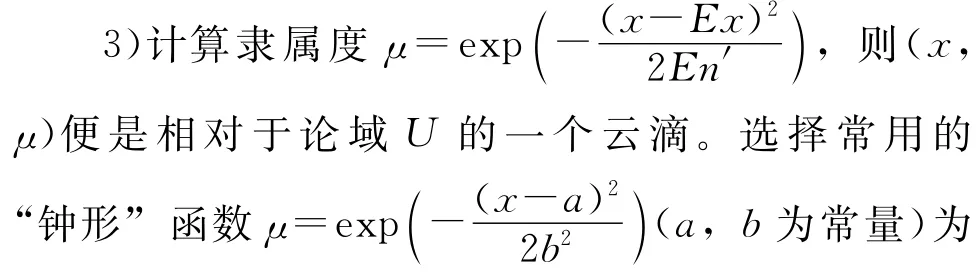
4)重复1),2),3)步骤直至生成足够的云滴。

对应的,逆向云发生器是用来计算云滴的数字特征(Ex,En,He)的,假设样本x的容量为n,其触发机制:

1)计算样本均值¯X和方差S2;

2 三次样条法拟合

本文采用实测数据是潍日高速公路上一段D 级GNSS控制测量和四等水准测量所获得的数据。由于GNSS点呈线性布设时,可以采用曲线拟合的方法进行GNSS高程拟合[10]。从而求解出待测的高程异常值,本文采用三次样条曲线拟合,但是实际操作中发现对总体数据进行拟合后,由于数据较多,跨度较大,结果并不理想,因此采用一种按照控制点位置划分成组分别拟合的方法,得到九组不同的曲线,具体的操作方法为:选取101个控制点作为已知数据进行实验。1号,11 号,21号,…,91号作为第一组实验数据;2号, 12号,22号,…,92号为第二组数据;以此类推,9号,19号,29号,…,99号为第九组数据,共9组数据分别进行拟合。在测区边沿的两个控制点100号和101号点分别标记为P1、P2点: P1(3 930 860.556,525 676.225),高程异常为2.398 0 m;P2(3 937 486.385,525 742.296 0),高程异常为2.374 0 m。用三次样条法拟合函数对P1、P2点的高程异常值进行外推计算,得到9个高程异常值及其残差值,如表1:

表1 P1、P2点的高程异常值及残差值

对上表进行分析,对于P1点,第一组数据残差值相对较小,拟合效果比较好;对于P2点,第五组数据拟合效果最好。可以看出由不同的已知点用相同的方法拟合的曲线是有差异的,对于总体来说可能其中一条拟合曲线是较好的即内外符合精度都高,但是对于某一个特定的点,该曲线拟合效果可能不是最好的。所以在测区内选择一点只进行了GNSS测量,若只选择上述拟合曲线中的一条进行内插或外推计算是不可取的。

3 云模型优化分析

由前文分析可知,对于一个特定点,一条曲线拟合并不能使其拟合精度达到最高,因此本文提出用云模型的方法对高程异常进行处理分析,将P1、P2点在表1中的的高程异常进行云模型处理,用Matlab软件编写云模型程序,得到图1、图2。

图1 点高程异常云模型

如图,x轴表示高程异常分布,y表示确定度(意义是度量倾向的稳定程度),x轴的最大、最小值是根据高程异常值的数字特征随机产生,对定性概念的贡献是个小概率事件,可以忽略不计[9],在图1中,经过对九组数据处理,可以看出P1点确定值最高的点对应的横坐标,也就是P1点的高程异常值约为2.39 m,残差值约为-0.008 m。在图1中2.38对应的确定度约是0.6,2.36对应的确定度约是0.2,并不能理解为2.38比2.36要精确三倍,更为直接的理解是2.38比2.36更精确,如图2,P2点确定度最高点对应的横坐标约为2.37 m,残差值为-0.004 m,经比较可以看出经过云处理的高程异常要比所有的曲线拟合更精确。

在测区范围取一点D(3 943 347.217,524 863.469)只进行了GNSS测量而没有进行水准测量,高程异常根据实测值进行内插,前文已经分析到,对于某一特定点,对于九组拟合的曲线,实验结果会有所差异,如表2所示:

图2 点高程异常云模型

表2 D点高程异常值表

在表2中,我们并不能确定哪一个高程异常更准确,这时我们就可以使用云模型对D点的高程异常值进行云处理,由图3可以看出云形的最高点所对应的横坐标为2.32,所以说D点高程异常的期望是2.32 m,是论域的中心值,最能够代表这个定性概念的点,反映在云形上就是云的“最高点”,即隶属度为1的点[11],由前文分析可以得出D点的高程异常为2.32 m较为可信。与图1和图2相比图3的离散程度更高,反映在云形上就是云的“厚度”更厚,超商越大,云越厚。

4 结束语

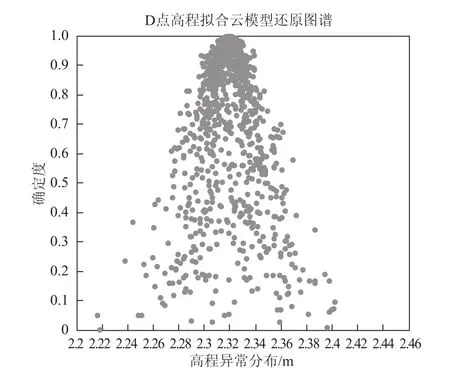
图3 D点高程异常云模型

已知点较多时,同时选用较多已知点做拟合,效果并不一定是最精确的;选用不同的已知点做拟合会生成不同的拟合曲线,产生不同的结果;对于一条拟合曲线并不能使所有的内插或外推点的拟合精度都高;对于某一个未进行水准测量的点,并不能确定哪一条曲线的拟合精度更高。云模型能通过定性和定量的方法对不同曲线拟合的结果分析优化,形成隶属云,而隶属云的形状能反映出整体特性,更好地进行高程异常的分析,使高程异常结果更为准确,可信。

[1] 宁津生,罗志才,李建成.我国省市级大地水准面精化的现状及技术模式[J].大地测量与地球动力学,2004,24(1):5-8.

[2] 张小红,程世来,许晓东.基于Kriging统计的GPS高程拟合方法研究[J].大地测量与地球动力学,2007,2(27):48-51.

[3] 郏红伟.GPS水准测量应用探讨[J].测绘通报,2005(8):29-31.

[4] 郭秦.GPS高程转换拟合方法及其辅助程序设计[D].成都:成都理工大学,2012.

[5] 卢辉,刘长星.MATLAB在GPS高程拟合中的应用[J].测绘科学,2009,34(2):191-193.

[6] 卓金武,李必文,魏永生,等.MATLAB在数学建模中的应用[M].2版.北京:航空航天大学出版社,2014.

[7] 陈贵林.一种定性定量信息转换的不确定性模型-云模型[J].计算机应用研究,2010,27(6):2007-2010.

[8] 王寅杰.云模型理论研究及其在彩色图像聚类分析中的应用[D].兰州:兰州交通大学,2013.

[9] 付斌,李道国,王幕快.云模型研究的回顾与展望[J].计算机应用研究,2011,28(2):420-426.

[10]岳仁宾.GPS高程拟合模型及其应用研究[D].重庆:重庆大学,2008.

[11]叶琼,李绍稳,张友华,等.云模型及应用综述[J].计算机工程与设计,2011,32(12): 4198-4201.

Applications of Cloud Model in GNSS Height Fitting

ZHANG Xinjie,LUAN Yuanzhong,ZHU Chunqiang
(Shandong University of Science and Technology,Qingdao 266510,China)

Focusing on the limitations of the curve fitting method in evaluating local area elevation,the paper proposes a new method that is based on the cloud model to analysis the height anomaly intuitive.The paper processes the curve fitting method on the basis of the position group of the control point,draws the cloud chart which is made according to the qualitative and quantitative analysis of the height anomaly,and shows the height anomaly features intuitively.As it turned out,the new method makes the results of height anomaly more reliable and validates the reliability of GNSSin elevation control.

GNSS height fitting;cloud chart;cloud model;height anomaly

P228

A

2095-4999(2015)-04-0110-04

2014-10-16

张欣杰(1990—),男,山东青岛人,硕士生,研究方向为大地测量与工程测量。

张欣杰,栾元重,朱纯强.云模型在GNSS高程拟合中的应用[J].导航定位学报,2015,3(4):110-113.ZHANG Xinjie,LUAN Yuanzhong,ZHU Chunqiang.Applications of Cloud Model in GNSS Height Fitting[J].Journal of Navigation and Positioning,2015,3(4):110-113.

10.16547/j.cnki.10-1096.20150422