不同星历和钟差产品的精密单点定位结果分析
何 帆,高成发,潘树国,靳晓东
(1.东南大学交通学院,南京 210096;2.东南大学仪器科学与工程学院,南京 210096)
不同星历和钟差产品的精密单点定位结果分析
何 帆1,高成发1,潘树国2,靳晓东1
(1.东南大学交通学院,南京 210096;2.东南大学仪器科学与工程学院,南京 210096)
针对由于国际全球导航系统服务网站提供的星历和钟差产品精度、采样率不同,导致最终定位结果存在差异的问题,提出了基于不同星历和钟差产品组合的精密单点定位方法,该方法利用不同产品提供的卫星坐标和卫星钟差进行精密单点定位解算,比较分析最终定位结果的稳定性和收敛速度等。研究结果表明,最终精密星历和最终精密钟差产品得到的定位精度最高,13.25 min的定位误差能够收敛到10 cm,1 d的定位精度高于1 cm;快速精密产品的定位精度相对较低, 42.86 min定位精度达到10 cm,在N、E、U方向精度分别降低50.5%、55.9%、92.8%;超快速预报产品的收敛速度最慢,定位精度最低。钟差产品的采样率和精度对收敛速度、稳定度影响较大,星历产品精度对最终定位误差产生影响。
静态精密单点定位;精密星历;精密钟差;收敛速度
0 引言
全球卫星导航系统(global navigation satellite system,GNSS)已经在各行各业中得到了广泛应用。精密单点定位(precise point positioning, PPP)是20世纪70年代美国子午卫星时代针对Doppler精密单点定位提出的概念[1]。与传统的单点定位采用广播星历相比,是利用国际GNSS服务局(international GNSS service,IGS)等组织提供的精密星历和精密卫星钟差等产品,进行的高精度定位[2]。不同的精密产品得到的定位结果存在差异,根据各组合形式得到的定位结果,能够为实际应用提供依据。
IGS提供的精密产品包括最终精密星历和钟差产品(IGS final product,IGF)、快速精密星历和钟差产品(IGS rapid product,IGR)、超快速精密星历和钟差产品(IGS ultra-rapid product, IGU)[3]。IGF钟差包含30 s和5 min两种采样率的钟差产品[4],IGU不提供单独的钟差文件。目前,已有诸多学者对使用IGS不同产品的精密单点定位解算结果进行了相关研究。例如:文献[5]利用IGS不同产品进行单天静态解算,定位精度基本相当,对于单历元动态解算,高采样率的钟差产品能显著提高其定位精度;文献[6]利用IGU预报轨道结合实时估计的卫星钟差得到的定位精度可达厘米级,较IGU预报钟差精度在X、Y、Z三个方向分别提高87.1%、81.8%、91.3%,可达厘米级定位精度,其收敛时间也缩短一半。
不同的IGS产品在精度、时延、更新率以及采样率方面差异较大[7],具体指标如表1所示。在实际生产作业和科研实践中,对定位精度与时延要求是各不同的,因此,研究不同IGS产品组合对精密单点定位结果的影响,并以此为依据选取合适的IGS产品以满足的实际需求,是十分必要的。为此,本文针对IGS精密星历和精密钟差设计6种组合,对多个IGS测站的单天观测数据进行解算,分析不同组合对静态定位精度的影响,为实际应用提供相关依据。
1 定位原理与数据
1.1 传统模型
精密单点定位有多种数学计算模型,如传统模型、UofC模型、无模糊度模型等[8]。
本文将采用传统模型作为精密单点定位的数学计算模型。传统模型采用双频全球定位系统(global positioning system,GPS)伪距和载波相位观测值的无电离层组合来构成观测模型[9],观测值中的电离层延迟误差一阶项通过双频信号的“消电离层组合”进行消除;对流层延迟误差分为两部分,干延迟通过GPT模型改正,湿延迟作为未知参数进行估计;接收机钟差未知参数进行估计,观测方程如式(1)所示:

1.2 数据来源
本次试验选取2014-06-25,15个IGS站的观测数据,观测时间长度为24 h,采样率为30 s,测站坐标以IGS提供的周解坐标作为真值。从IGS网站下载相应时间的IGS星历和采样率为30 s的钟差、IGR星历和钟差、IGU实测和预报星历。由于IGS网站没有提供单独的IGU精密钟差产品,故不对IGU预报钟差进行分析。IGU预报星历在每天的UTC 00时、06时、12时及18时发布,并存在3~9 h的时间延迟。文中的IGU星历实测部分为UTC00时发布的IGU实测部分,IGU星历预测部分为上述四个时刻的IGU文件预测部分组合而得。
目前,IGS发布产品的精度、时延和采样率参数如表1所示。
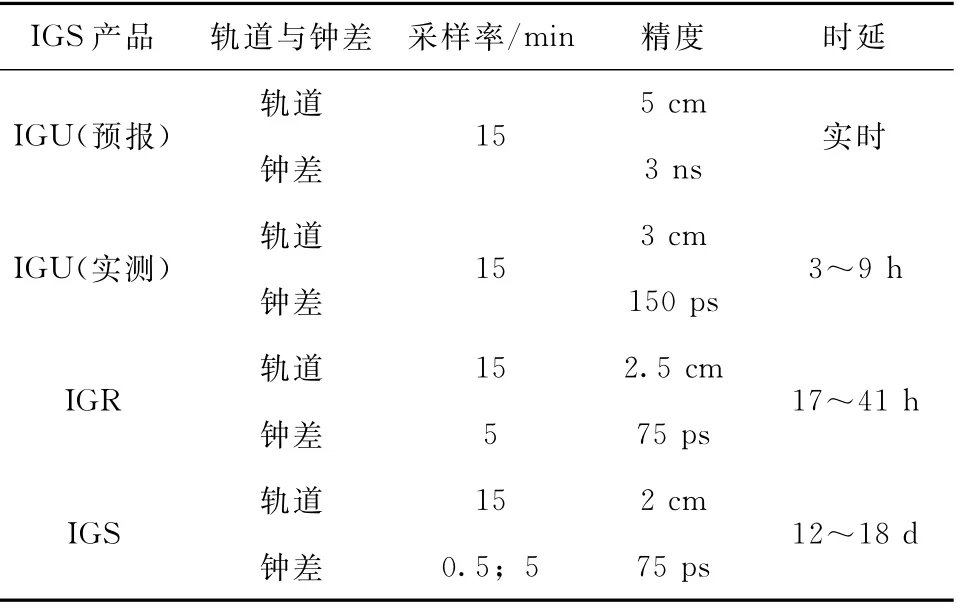
表1 IGS产品参数
精密星历产品中,IGS星历精度最高,其次依次是IGR星历,IGU星历实测部分,IGU星历预测部分。其中IGS星历、IGR星历、IGU星历实测部分精度相差较小,IGU星历预测部分精度明显劣于前者。
精密钟差产品中,IGS钟差分5 s和30 s采样率两种产品,其精度与IGR钟差产品相当。IGU钟差预测部分精度较差,只有前者的1/2。
本算例采用的观测文件采样率为30 s,进行定位时,需要通过内插得到观测时刻的轨道和钟差参数。对于采样间隔大于30 s的精密文件,通常采用拉格朗日多项式或切比雪夫多项式内插法[10],得到所需的采样率产品,本文采用十一阶拉格朗日插值函数。为了分析使用IGS不同星历和钟差产品组合精密单点定位的定位结果,对不同产品设置了6种组合形式,分别进行解算,具体组合如表2所示。

表2 IGS不同星历和钟差组合
因为现阶段尚无单独的IGU钟差文件,且IGU星历提供的钟差精度较低,采样率为15 min,无法满足解算需求,故关于IGU星历的组合皆使用了IGS钟差。
2 单个测站算例分析
以C++语言为开发平台,自主开发定位解算程序,计算出IGS测站在不同组合下N、E、U三个方向的定位误差值。本文中定义当定位误差小于10 cm时,定位结果收敛;最后一个历元坐标解算值与测站真值的差值作为定位误差。限于篇幅,从15个测站中任选一站(AREQ站)作为算例,绘制出该站在6种组合下的定位误差曲线图(误差曲线图纵坐标取值范围为-10 cm~+10 cm)。
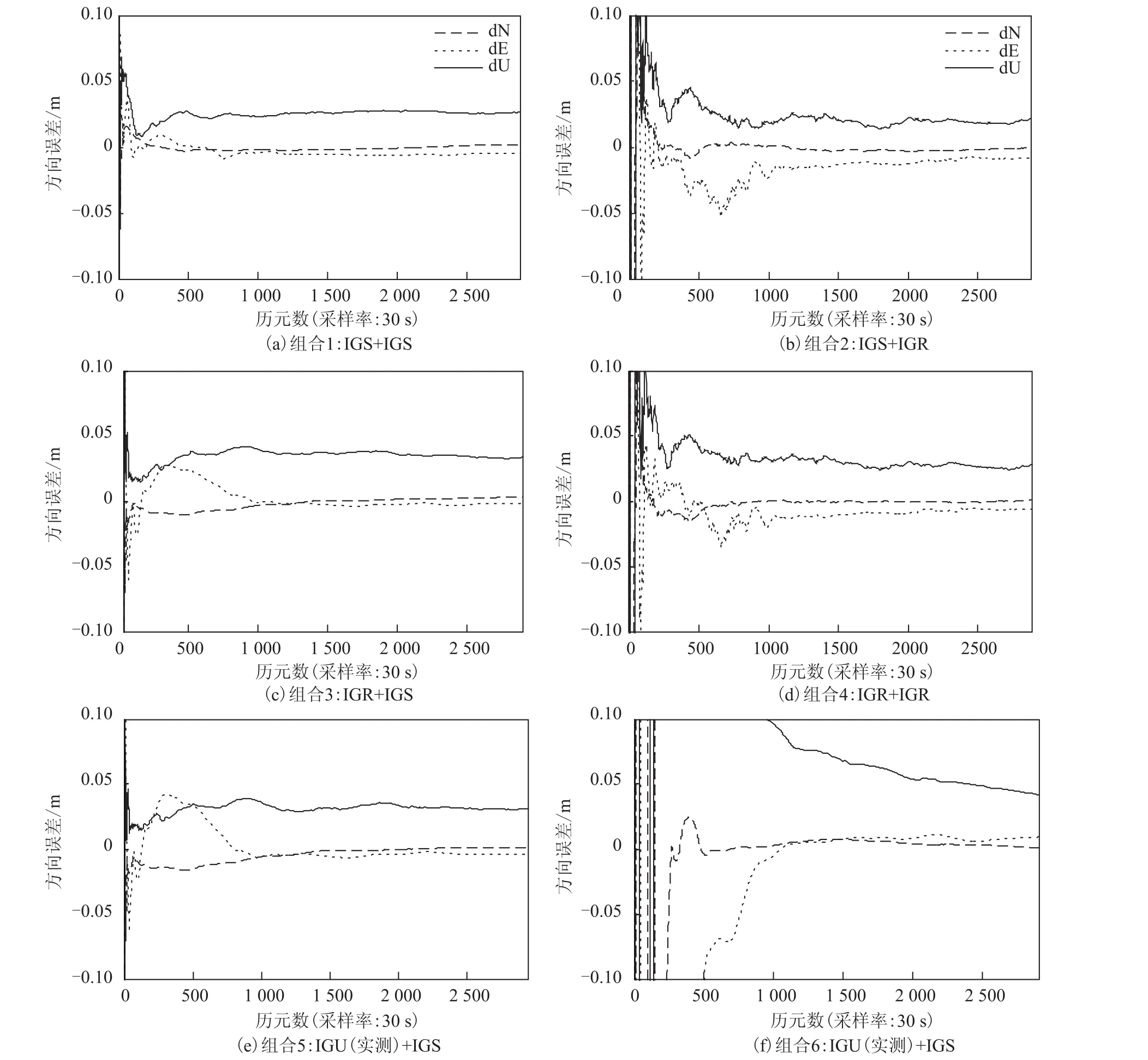
图1 测站AREQ在6种组合下的定位误差
在图1中,图1(a)~图1(f)分别表示AREQ测站在组合1至组合6共六种情况下所得定位解算结果。分析图1,可知:
1)分别对比图1(a)和图1(b),图1(c)和图1 (d)可看出,在使用相同的精密星历情况下,使用IGR钟差的定位结果较使用IGS钟差在收敛速度方面也较慢;稳定度方面较差,尤其是在定位初期抖动幅度较大;最终定位误差方面差异较小。分析可知,虽然IGS钟差与IGR钟差精度相当,但是IGR钟差采样率远大于IGS钟差,故IGR钟差插值所得卫星钟差精度要差于IGS钟差插值效果。
2)比较比较图1(a)、图1(b)、图1(c)及图1 (d),4图对应组合星历方面分别使用IGS星历、IGR星历、IGU星历实测部分和IGU星历预测部分,钟差方面皆使用IGS钟差。IGR星历较IGS星历,轨道标称精度差5 mm,使得组合3较组合1在N、E、U方向的最终定位误差差1.40 mm、2.19 mm、5.92 mm。IGU星历实测部分轨道标称精度较IGR星历差5 mm,故组合5较组合3在N(北)、E(东)、U(高)方向的最终定位误差差2.43 mm、1.60 mm、2.40 mm。IGU星历预测部分轨道标称精度最差,其误差曲线图亦明显较差,故不参与比较。
3)根据产品发布时间,比较图1(a)、图1 (d)、图1(e)和图1(f),可知组合1的定位精度最高,收敛速度最快,并具有较好的稳定度;组合4的定位精度、收敛速度略差于组合1,定位初期稳定度明显差于组合1,定位后期稳定度有所提高;组合5定位精度和收敛速度差于组合4,稳定度高于组合4;组合6在使用IGS钟差的情况下,定位精度、收敛速度明显较差,尤其是U方向需要较长时间收敛。
综上所述,在使用相同星历,不同钟差条件下,最终定位误差方面不存在较大差异,而随着钟差精度的降低,收敛速度变慢,稳定度尤其是在定位初期明显下降;使用不同星历,相同钟差条件下,使用IGS星历、IGR星历、IGU星历实测部分的最终定位误差依次降低约2 mm。由此可知,钟差文件精度对于定位的收敛速度和稳定度有较大影响,而星历文件的精度对定位误差有显著影响。
从IGS提供的星历和钟差产品发布时间来看,在两至三天内,若用户可以自行计算高精度卫星钟差,结合IGU轨道实测部分,定位结果能达到较高精度;使用IGR星历和IGR钟差,定位结果亦能达到较高精度,但是定位初期稳定度较差。若用户可以等待较长时间,使用IGS星历和IGS钟差,定位结果最优。使用IGU星历预测部分结合IGS钟差,定位结果收敛时间长且定位精度较低。
3 多个测站算例分析
为了进一步比较6种组合形式得到的结果,在收敛速度和定位精度两方面的具体指标,对15 个IGS站的定位结果进行了统计,得到每个测站24 h的定位结果(定位结果为最后一个历元坐标解算值与测站真值的插值),具体结果如图2所示。
图2由上到下分别表示N、E、U三个方向, 15个测站在6种组合下,收敛后的结果误差值的均方根(root mean square,RMS)。可以直观地看出,测站在6种组合情况下,各个方向定位误差的RMS均小于3 cm;其中组合1至组合3在平面和高程方向均能够达到优于1.5 cm的定位精度,达到较高精度的静态定位结果。
水平方向上组合6对应的误差RMS显著大于组合1至组合5的五种组合,其中E方向误差RMS普遍大于对应测站的N方向RMS值。U方向上,各测站的误差RMS各异,各种组合之间不存在显著差异。此外,GLSV、MIKL测站在组合6下得到的定位误差最大,N、E、U的误差RMS均大于1.5 cm。
不同测站的定位结果不同,为了分析比较不同组合的效果,将15个测站的定位误差数据及收敛时间进行统计整理列于表3。表3中RMS表示误差均方根值,Δ表示最后一个历元的定位误差值。
由表3可以看出:
(1)对于N、E、U三个方向的误差RMS,当采用IGS钟差,星历为IGS星历或者IGR星历时,RMS值均小于1 cm;星历为IGU星历, RMS值大于1 cm,且星历为IGU预测星历的解算RMS值明显大于使用IGU实测星历解算所得RMS值。可知当星历轨道标称精度越高,定位误差RMS越小;IGS星历和IGR星历能满足高精态定位需求。
(2)对于最后一个历元的定位误差值,组合1至组合5平面方向均在5 mm以内;U方向定位精度明显劣于平面方向,约为30 mm。因为大气误差、天线改正等因素影响,解算U方向定位精度较低,尚需进一步优化误差改正模型。
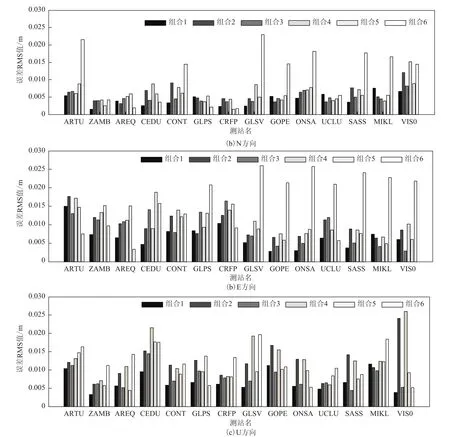
图2 各测站在不同组合下的结果
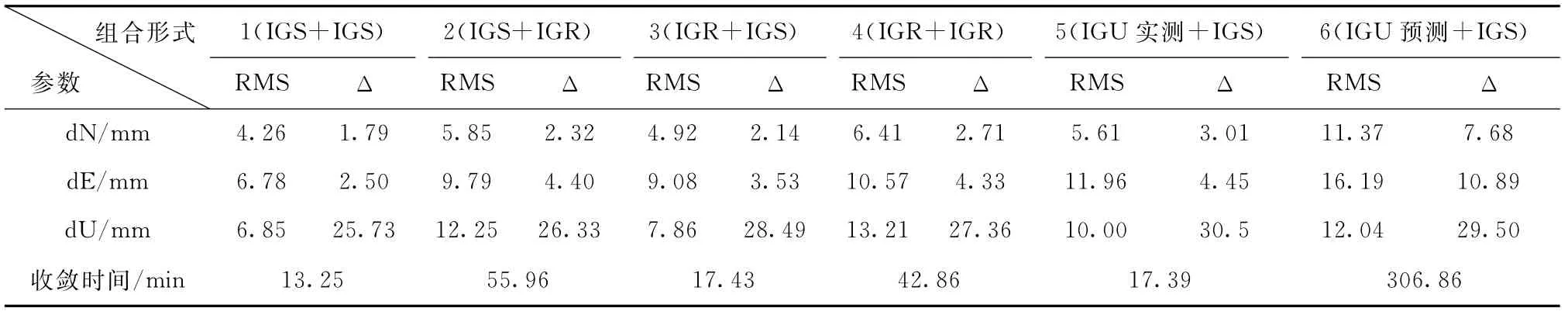
表3不同组合精密产品得到的定位结果
(3)就收敛时间而言,组合1的收敛时间最短,平均值为13.25 min。采用IGS星历和IGR钟差的组合2,其收敛时间是组合1的4.22倍,采用IGR星历和IGS钟差的组合3,其收敛时间是组合1的1.31倍。故可知钟差文件的采样率和精度对定位的收敛速度影响大于星历文件。
(4)对比组合4和组合5,可发现使用IGU星历实测部分和IGS钟差时,RMS值和定位误差值与使用IGR星历和IGR轨道结果相近,收敛时间显著缩短。结合各测站定位误差曲线图,可知组合5的误差曲线稳定度较组合4高。现阶段关于反演钟差的技术逐渐成熟,故可以自主估计卫星钟差的用户可以将钟差与IGU星历实测部分结合在较短时间内进行解算。
4 结束语
对于IGS网站上提供的三种星历产品及其钟差数据,进行静态定位均能达到较高精度。
IGS星历和30 s采样率的IGS钟差产品得到的定位精度最高,水平和高程方向均能达到毫米级精度。IGR钟差与IGS钟差精度相当,但是因为其采样率为5 min,远大于IGS钟差的30 s采样率,插值计算所得卫星钟差精度较低,致使使用IGR钟差进行定位,定位误差值较大,定位稳定性有所下降。IGU预报星历轨道误差值较大,即使与精度较高的IGS钟差共同解算,定位结果较差,且U方向需要较长时间才能收敛。所以为了使IGU星历满足工程应用需求,IGU星历尚需进一步提升其轨道精度。用户需根据不同精密产品组合的定位结果分析,合理选择合适的精密星历和精密钟差产品。
现阶段使用IGS或IGR星历,IGS钟差或IGR钟差进行解算均能达到较高定位精度,但是IGS星历或钟差,IGR星历或钟差均存在一定时间的时延,无法满足部分工程实时性要求。用户可使用IGU星历结合实时钟差进行解算。
[1] ZUMBERGE J F,HEFLIN M B,JEFFERSON D C,et al.Precise point positioning for the efficient and robust analysis of GPS data from large networks[J].Journal of Geophysical Research:Solid Earth(1978-2012),1997,102(B3):5005-5017.
[2] 李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009.
[3] 史线龙,郑勇,马国元,等.不同星历和钟差产品对车载定位的影响分析[J].测绘工程,2011,20(6):28-31.
[4] HÉROUX P,KOUBA J.GPS Precise point positioning using IGS orbit products[J].Physics and Chemistry of the Earth, Part A:Solid Earth and Geodesy,2001,26(6):573-578.
[5] 娄俊萍,李文文,陈克杰.不同IGS产品对精密单点定位的影响[J].测绘地理信息,2013,38(4):21-23.
[6] 江楠,徐天河,许艳.一种无需精密钟差的实时精密单点定位方法[J].中南大学学报(自然科学版),2013,44(11): 4520-4526.
[7] 李鹏,沈正康,王敏.IGS精密星历的误差分析[J].大地测量与地球动力学,2006,26(3):40-45.
[8] 蒲崛茜.精密单点定位相关技术问题研究[D].成都:西南交通大学,2012.
[9] 吴峰.GPS精密单点定位导航方法研究[D].广汉:中国民用航空飞行学院,2009.
[10]常志巧,郝金明,张成军.GPS精密星历的外推精度分析[J].测绘工程,2006,15(2): 27-29.
Research on Results of Precise Point Positioning with Different Ephemeris and Clock Bias Products
HE Fan1,GAO Chengfa1,PAN Shuguo2,JIN Xiaodong1
(1.School of Transportation,Southeast University,Nanjing 210096,China; 2.School of Instrument Science and Engineering,Southeast University,Nanjing 210096,China)
Due to the ephemeris and clock bias products have different accuracy provided by International GNSS(Global Navigation Satellite System)Service,the question for final positioning results are different based on them.The method of precise point positioning based on different ephemeris and clock bias products is proposed.In this method,satellite coordinates and satellite clock bias are provided by different products for precise point positioning,and the stability and convergence speed of final positioning results are compared and analyzed.The research results show that the positioning accuracy of results with final precise ephemeris and final precise clock bias products is the highest,which converges to 10cm in 13.25 minutes,and the positioning accuracy in one day is higher than 1cm.The positioning accuracy of tests with rapid precise products is relatively lower,which can reach 10 cm in 42.86 minutes,and the positioning accuracy in NEU directions decreased by 50.5%、55.9%、92.8%respectively.The convergence speed of the result with ultra-rapid predicted products is the slowest,and the positioning accuracy is the lowest.The sampling rate and accuracy of precise clock bias have a great impact on the convergence speed and stability,and the precise of ephemeris products can affect the final accuracy of precise point positioning.
precise point positioning;precise ephemeris;precise clock bias;convergence speed
P228
A
2095-4999(2015)-04-0079-06
2014-10-16
中央高校基本科研业务费专项(SJLX_0088),江苏省普通高校研究生科研创新计划资助项目(SJLX_0088)。
何帆(1992—),女,四川绵阳人,硕士,主要研究方向为GNSS卫星导航定位。
何帆,高成发,潘树国,等.不同星历和钟差产品的精密单点定位结果分析[J].导航定位学报,2015,3(4):79-84.HE Fan,GAO Chengfa,PAN Shuguo,et al.Research on Results of Precise Point Positioning with Different Ephemeris and Clock Bias Products[J].Journal of Navigation and Positioning,2015,3(4):79-84.
10.16547/j.cnki.10-1096.20150415

