云过程神经网络模型及算法研究

王 兵李盼池杨冬黎于晓红

①(东北石油大学计算机与信息技术学院 大庆 163318)

②(大庆油田公司勘探开发研究院 大庆 163712)

云过程神经网络模型及算法研究

王 兵*①李盼池①杨冬黎①于晓红②

①(东北石油大学计算机与信息技术学院 大庆 163318)

②(大庆油田公司勘探开发研究院 大庆 163712)

该文针对输入输出具有不确定性特征并与时间或过程有关的复杂非线性系统建模和求解问题，利用过程神经网络对时变信号的动态处理能力，结合云模型对定性定量概念的转化能力，构建了一种具有不确定性信息处理能力的云过程神经网络模型，并采用猫群优化算法同时对网络结构和参数进行并行优化设计，提高了网络逼近及泛化能力，实现了神经网络在时间域和不确定信息处理领域上的有效扩展。仿真实验结果验证了模型和算法的可行性和有效性。

云模型；云过程神经网络；猫群优化；时间序列预测

1 引言

过程神经网络是本世纪初由何新贵院士等人[1]提出的一种新的人工神经网络模型。它的输入、输出以及连接权等均可为与时间或过程有关的函数，其聚合运算和激励可同时反映时变输入信号的空间加权聚合以及在时间轴上的累积效应，对于求解与时间过程有关的信息处理问题具有广泛的适用性。对于过程神经元网络的训练问题，文献[2-4]分别提出了基于函数基展开结合最小均方算法、基于数值积分以及基于智能优化计算的训练方法，有效简化了时空聚合运算。在网络性能方面，文献[5,6]研究了其连续性、可逼近性及计算能力等理论性质。在模型构造方面，文献[7-9]先后提出了小波，Elman，量子等多种过程神经网络模型。过程神经网络也被广泛应用于发动机排气温度监测[7]，PID控制[10]，图像处理[11]等领域。

客观世界中绝大部分事物和现象都具有不确定性，神经网络只能表达和处理精确、定量化的信息模式，很难应付自然界中的随机性和模糊性信息。云模型的出现[12]提供了一种新的定性定量不确定性转换模型，已经在不确定性推理、智能控制、决策支持、系统预测等方面得到成功应用[13]。目前，国内外很多学者致力于将云模型与神经网络进行融合并已提出一些有意义的云神经网络模型。

针对具有过程性、随机性和模糊性特征的复杂非线性系统的建模和求解问题，本文将云模型对定性定量概念的转化能力与过程神经网络对时变信号的处理方法相结合，提出了一种云过程神经网络模型(Cloud Process Neural Network, CPNN)，实现了神经网络在时间域和不确定信息处理领域上的扩展。此外，文中采用猫群优化算法对网络结构和学习参数进行并行优化设计，提高了网络的逼近及泛化能力。将该模型算法用于个人家庭电力消耗数据预测，实验结果验证了模型和算法的可行性和有效性。

2 云过程神经网络模型

本文建立的输入输出均为云化模型的云过程神经网络由时变输入层、过程云化层、规则层、标准化层、整合层、逆向云化层和输出层组成。本文着重研究多输入/单输出结构的网络系统，由此不难推广到多输入/多输出系统，其拓扑结构如图1所示。该网络模型表达的云推理规则的一般形式为

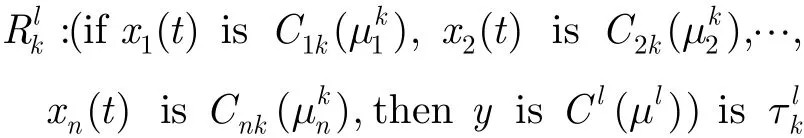
(1)时变输入层：负责将时变过程输入信号的每一个分量传递到过程云化层进行云化处理。设网络输入空间为([0,])n

CT，其中[0,T]为时间过程采样区间。n个过程式输入节点组成的输入函数向量为

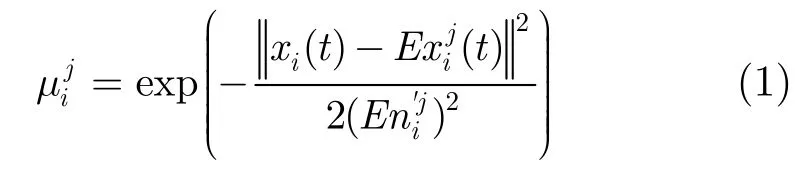
(3)规则层：每个节点代表“软与”操作，执行云规则匹配，并确定该条规则的激活度ak，其中“软与”操作可通过多维正态云模型为网络“软与”程度的调节参数。

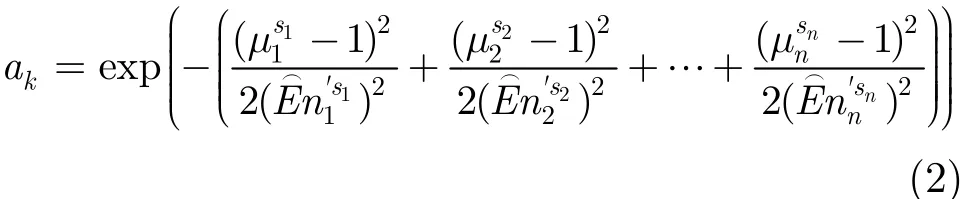
(4)标准化层：对规则层传递来的激活度ak进行标准化操作。

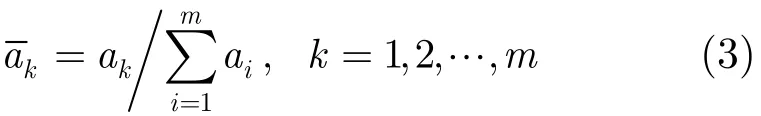
(5)整合层：负责对每条规则的平均激活度进行整合输出：

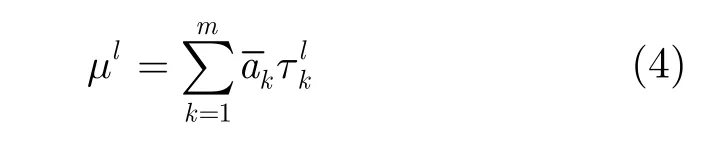
其中l=1,2,…,q 为网络输出y所分解的子云数量。μl为每个子云的确定度。为第k条规则结论为Cl(μl)的可信度。由于所以μl∈[0,1]。

(6)逆向云化层：每个节点代表一个云模型，负责对特定隶属度μl进行逆向求解(Y条件云发生器)：

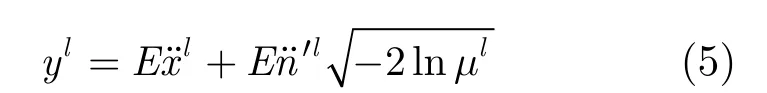
(7)输出层：采用加权平均法进行输出：

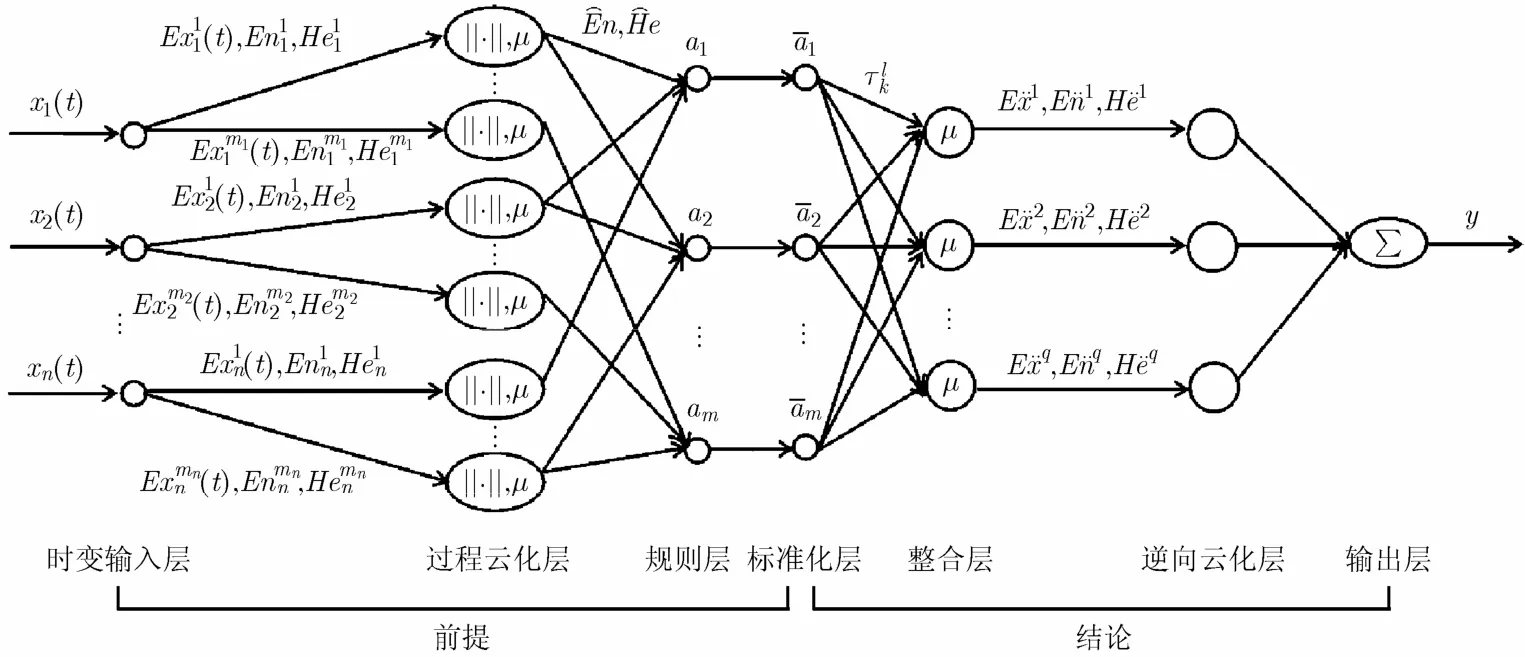
图1 云过程神经网络模型

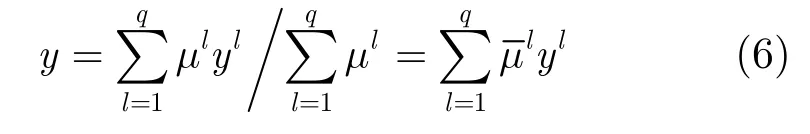
可以看出，该网络为多层前馈型网络，有4组权参数需要调整，即过程云化层中的规则层中的整合层中的逆向云化层中的从时变输入层到标准化层实现规则的前提部分，从整合层到输出层实现规则的结论部分。

3 云过程神经网络学习算法

对于云过程神经网络的训练问题，可以采用传统的基于基函数展开结合梯度下降的学习算法[3]，但该方法中选用何种基函数以及如何确定基函数的展开项数还没有一个统一的指导标准。此外，梯度下降法也容易陷入局部最优，而且还可能面临梯度不可计算的情况。实际上，过程神经网络除了参数学习之外还应包含对网络结构的学习，即学习过程应涉及结构调整和参数调整两大部分，传统的依据经验法或试凑法对网络结构进行的调整往往存在很大的误差。因此，文中将采用一种新的基于群体行为的智能优化算法 猫群优化算法(Cat Swarm Optimization, CSO)[14]在有效确定网络最优结构的同时优化网络学习参数，使网络能够快速、准确地获得全局最优解。

3.1 适应度函数的设计

其中，ys可根据式(1)-式(6)计算求得。

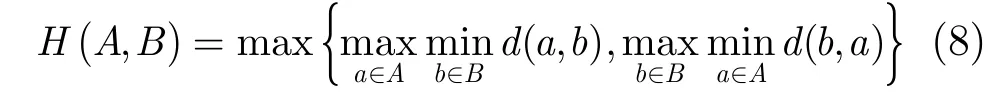
在实际工程中，网络输入多为由采样得到的离散时间序列，因此，可直接输入进行Hausdorff距离计算。当系统输入为时变函数时，可对函数进行离散化处理后再计算。设在时间过程采样区间[0,T]上有P个采样点，则网络输入函数离散化为相应地将也表示为离散化形式作为网路的待调参数。

综上所述，云过程神经网络的训练目标函数E为结构参数mi,q和变参数的函数。采用云过程神经网络的训练目标函数E作为猫群算法的适应度函数，从而将云过程神经网络的训练问题转化为最小化网络目标函数E的优化问题。

3.2 具体学习步骤

步骤1 初始化：确定猫群规模N，最大迭代次数T，设置当前迭代次数t=0。随机生成N只猫的初始位置和速度信息。猫的位置信息可以表示为

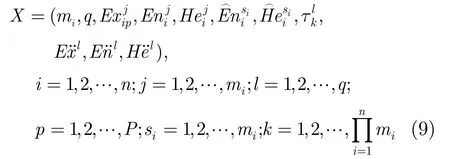
则猫的位置维度为

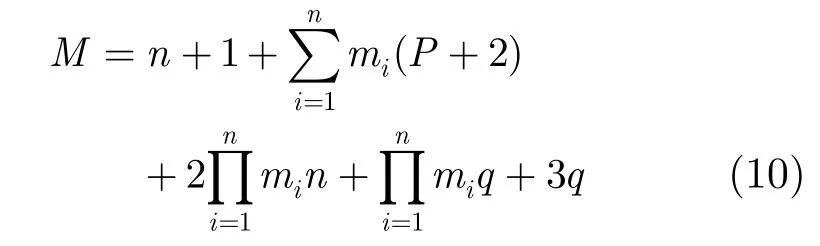
步骤 2 分配：按照混合比例算子MR的值分配少部分猫进入追踪模式，其它的猫进入搜寻模式。

步骤3 评价：通过适应度函数计算每只猫的适应度值。记录到目前为止获得的猫的最佳位置为

步骤4 移动：根据猫的工作模式标志信息分别移动猫的位置如下：

(1)搜寻模式：

(a)复制：将当前猫c的位置复制SMP份放入记忆池中。如果自身位置考虑因子SPC为真，则当前猫c的位置作为一个候选位置放入记忆池中，其它(SMP-1)份保持不变。

(b)变异：对于每一个位置副本，首先根据维数变化因子CDC选择M维度中的若干维参加变异操作，在当前值基础上随机加减一定百分比代替原有值，新旧值变化幅度必须在维度变化域因子SRD限定范围内。

(c)评价：根据适应度函数计算猫c各个候选位置的适应度值FS。

(d)计算：根据式(11)计算每个候选位置的选中概率；如果选中概率全部相等，则将其均置为1。

(e)移动：根据各个候选位置的选中概率，采用轮盘赌方法选择其中一个候选位置作为猫c新的当前位置进行移动。

(2)追踪模式：

(a)根据式(12)更新当前猫c的速度信息。

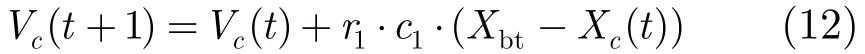
其中c1为一常量，r1是[0,1]范围内的一个随机数。

(b)检查更新后的每一维速度分量是否仍在设定的最大速度Vmax内。如果不在，那么这一维的速度分量就被限定为Vmax。

(c)根据式(13)更新当前猫c的位置信息。

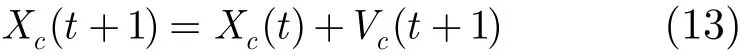
步骤5 判断：若t＞T或目标函数E小于设定值，则停止运算。否则t=t+1，转步骤2。 3.3 学习算法分析

在上述学习算法中，对猫的搜索空间的合理限定是充分发挥该算法同时优化网络结构和学习参数的保证。mi, q为样本的输入输出分解为子云的数量，属于结构信息，取值为正整数。在一次实验中n, P是固定不变的，因此猫的位置的维度大小由mi, q决定。如果mi, q取值过大，待优化变量过多，不但会给算法带来性能影响，甚至可能会产生维数灾难。mi, q过小，又会导致网络结构过于简单而没有足够的逼近能力。因此，需要根据实际问题的复杂程度设定一个合理的范围。此外，mi, q的频繁变动会引起其它待调参数维度的改变而导致没有充分的学习机会，可设定每迭代若干次后mi, q才有机会进行选择性移动。对于各子云的期望参数可以采用下面两种方法来确定其初值：一种是从各子云对应的输入或输出样本中随机选取部分样本作为各自期望的初始值；另一种方法是采用K-均值等聚类的聚类中心作为各子云的初始期望。云的熵和超熵取值为正实数，并且为防止雾化现象发生，超熵不能超过其相应熵的1/3。

猫群算法本身的搜索策略并不复杂，其计算复杂性在于每次迭代时都要为每只猫的每个候选位置或更新位置进行一次适应度评价，即计算网络学习目标函数E。因此该算法的计算复杂度主要受猫群规模N，迭代次数t以及记忆池大小SMP的影响，目标函数E的计算次数≤Nt (SMP+1)次。同时E本身的计算也与mi, q有关。可以通过合理设定N, t, SMP,mi, q的值或范围使算法在计算量和优化性能之间找到一个较好的平衡。

4 仿真实验

本次实验采用UCI数据集中的个人家庭电力消耗数据集进行仿真。该数据集收录了从2006年12月到2010年11月期间近4年某家庭每分钟的电力消耗情况，共计2075259个数据实例，常被用来检测时间序列时变样本的预测、分类能力。

实验拟分别进行电力消耗功率小时数据、日数据、周数据和月数据的单步短期预测。以分钟采样数据为基础分别计算获得34560, 1440, 205和46份完整的小时、日、周和月数据。其中周数据如图2所示。

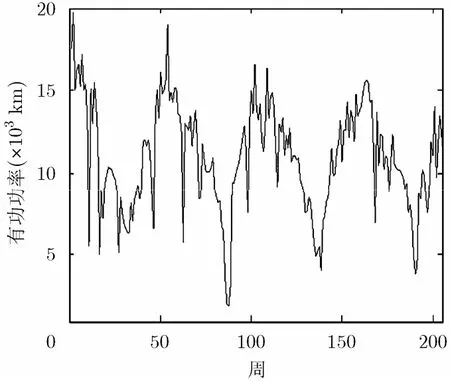
图2 周时间序列数据

以周数据预测为例，预测方案是用前d周的周数据预测第d+1周数据。实验中将数据集按5︰2.5 ︰2.5的比例随机分为训练集、验证集和测试集。为体现本文提出的云过程神经网络及其学习算法的优越性(CPNN-CSO)，分别将其与普通过程神经网络(PNN)和采用基函数展开结合梯度下降方法的云过程神经网络(CPNN)进行对比。由预测方案可知，3种网络的输入输出节点数均为1。经过试探法，小时、日、周和月预测对应的d值分别取为24, 10, 7 和4。对于PNN和CPNN，利用3次样条函数对网络d个输入离散采样点进行拟合并采用Walsh基展开。在CPNN-CSO算法中，猫群规模N=160，记忆池大小SMP=5，混合比例算子MR=0.05, mi, q的搜索空间限定为[1,8]之间的整数。3种网络的最大迭代次数均设定为1000，样本归一化后的均方根误差均限定为0.0001。经过多次实验对比分析，3种模型算法在训练集、验证集和测试集上的收敛误差对比如表1所示。

实验结果表明，无论是在模型逼近能力方面还是在网络泛化性能上，整体来说，CPNN-CSO均优于CPNN和PNN，其中PNN效果最差。对此结果可作如下分析：首先，CPNN-CSO和CPNN通过云模型将电力消耗定量数据转换为多个子云的定性概念，并通过挖掘多个子云之间的内在规律，确定输入输出变量之间的关联规则，从而很好地体现了客观事物的随机性、模糊性及相关性，因此预测能力比PNN有所提高。其次，与CPNN相比，CPNNCSO采用了猫群优化算法替代了传统的基展开结合梯度下降算法，并且同时从结构和参数两方面对网络进行辨识，充分发挥了猫群算法的局部搜索能力及全局优化能力，避免了梯度下降算法早熟带来的算法不稳定，因此效果较好。在CPNN-CSO算法中，最终确定网络输入输出软划分为子云的数量mi=5,q=3。以周数据预测为例，3种模型算法的预测结果对比如图3所示。

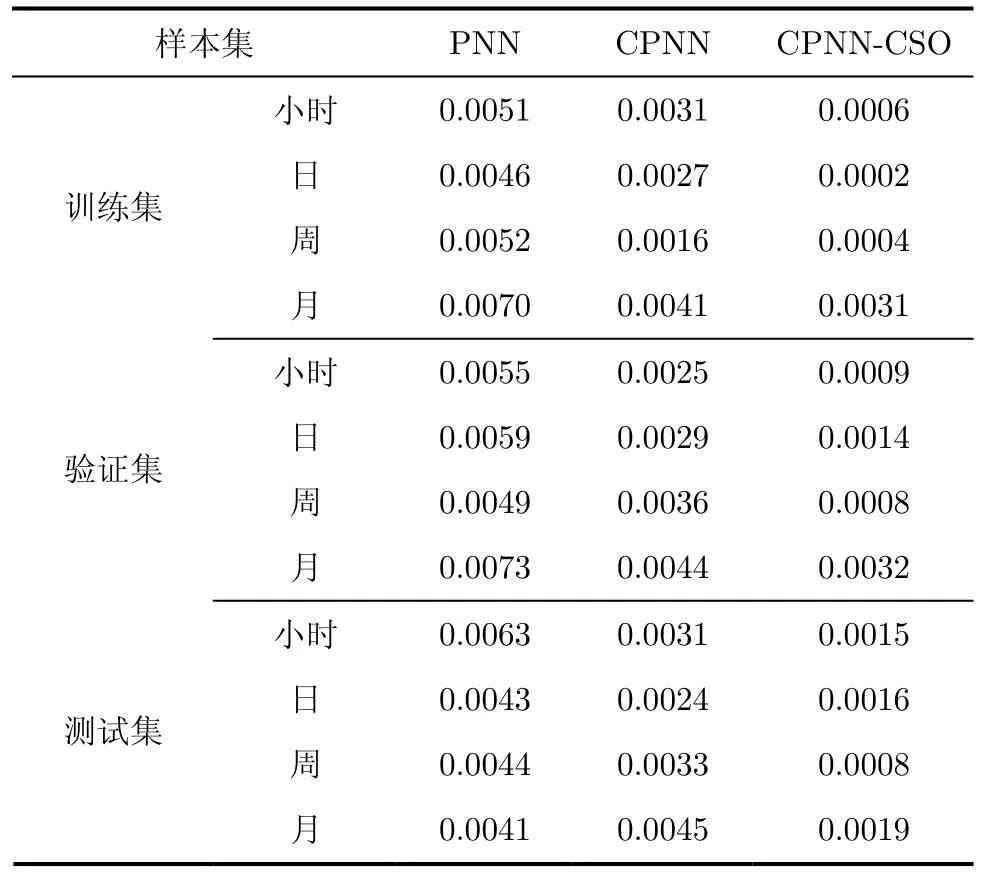
表1 3种方法在训练集、验证集和测试集上的收敛误差对比

文中利用3种模型算法对周数据进行一次训练和预测的平均耗时进行了实验分析。其中，PNN和CPNN所耗时间相差不大，分别为4.17 s和4.42 s。因为两种模型均为前馈模型，采用相同学习算法，只是待调参数个数有些差异而已。而CPNN-CSO耗时较多，为791 s。这是因为CSO算法中每次迭代都要对所有猫进行适应度评价，但多只猫之间的相互交流协作会更快更有效地找到最优点，从而减少算法的迭代次数，所以整体耗时仍是可以接受的。

图3 3种方法的预测结果对比

5 结束语

本文提出了一种基于云模型理论的云过程神经网络模型和算法，将云推理系统与过程神经网络有机结合起来，一方面实现了云推理系统的自学习和自适应特性，同时也增强了过程神经网络对自然界中持续性、随机性和模糊性过程式信息的动态处理能力，从而有效地弥补二者存在的不足。通过采用猫群优化算法提高了云过程神经网络的逼近和泛化能力，为时变信号的模式识别、过程预测等问题提供了一种新的解决方法。关于云过程神经网络的连续性、可逼近性、收敛性以及泛化能力等理论性质值得进一步进行深入研究。

[1] He Xin-gui and Liang Jiu-zhen. Process neural networks [C]. The 16th World Computer Congress 2000, Proceedings of the Conference on Intelligent Information Processing, Beijing, 2000: 143-146.

[2] 许少华, 何新贵. 基于函数正交基展开的过程神经网络学习算法[J]. 计算机学报, 2004, 27(5): 645-650. Xu Shao-hua and He Xin-gui. Learning algorithms of process neural networks based on orthogonal function basis expansion[J]. Chinese Journal of Computers, 2004, 27(5): 645-650.

[3] 肖红, 许少华, 李盼池. 基于数值积分的多聚合过程神经网络算法[J]. 信息与控制, 2013, 42(5): 608-612. Xiao Hong, Xu Shao-hua, and Li Pan-chi. Multi- aggregation process neural networks algorithm based on numerical integration[J]. Information and Control, 2013, 42(5): 608-612.

[4] 许少华, 何新贵. 一种基于混沌遗传与粒子群混合优化的过程神经网络训练算法[J]. 控制与决策, 2013, 28(9): 1393-1398. Xu Shao-hua and He Xin-gui. A training algorithm of process neural networks based on CGA combined with PSO[J]. Control and Decision, 2013, 28(9): 1393-1398.

[5] 何新贵, 梁久祯. 过程神经元网络的若干理论问题[J]. 中国工程科学, 2000, 2(12): 40-44. He Xin-gui and Liang Jiu-zhen. Some theoretical issues on procedure neural networks[J]. Engineering Science, 2000, 2(12): 40-44.

[6] 许少华, 何新贵. 关于连续过程神经元网络的一些理论问 题[J]. 电子学报, 2006, 34(10): 1838-1842. Xu Shao-hua and He Xin-gui. Some theoretical issues on continuous process neural networks[J]. Acta Electronica Sinica, 2006, 34(10): 1838-1842.

[7] Zhong Shi-sheng, Li Yang, and Ding Gang. Continuous wavelet process neural network and its application[J]. NeuralNetwork World, 2007, 17(5): 483-495.

[8] Ding Gang and Lin Lin. Elman-style process neural network with application to aircraft engine health condition monitoring[J]. Lecture Notes in Computer Science, 2011, 6675(1): 484-494.

[9] 李盼池, 王海英, 戴庆, 等. 量子过程神经网络模型算法及应用[J]. 物理学报, 2012, 61(16): 160303. Li Pan-chi, Wang Hai-ying, Dai Qing, et al.. Quantum process neural networks model algorithm and applications[J]. Acta Physica Sinica, 2012, 61(16): 160303.

[10] Wang Bing, Xu Shao-hua, Meng Yao-hua, et al.. A process neural network based on improved particle swarm optimization and its application in PID control[J]. International Journal on Advances in Information Sciences and Service Sciences, 2013, 5(7): 701-709.

[11] 肖红, 李盼池. 两种离散过程神经网络算法及在图像恢复中的应用[J]. 信号处理, 2013, 29(8): 1182-1189. Xiao Hong and Li Pan-chi. Two discrete process neural network algorithm with application to image restoration[J]. Signal Processing, 2013, 29(8): 1182-1189.

[12] 李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J]. 计算机研究与发展, 1995, 32(6): 16-18. Li De-yi, Meng Hai-jun, and Shi Xue-mei. Membership clouds and membership cloud generators [J]. Computer of Research & Development, 1995, 32(6): 16-18.

[13] 付斌, 李道国, 王慕快. 云模型研究的回顾与展望[J]. 计算机应用研究, 2011, 28(2): 420-426. Fu Bin, Li Dao-guo, and Wang Mu-kuai. Review and prospect on research of cloud model[J]. Application Research of Computers, 2011, 28(2): 420-426.

[14] Chu, S C, Tsai P W, and Pan J S. Cat swarm optimization[C]. Proceedings of the 9th Pacific Rim International Conference on Artificial Intelligence, LNAI, 4099, 2006: 854-858.

[15] Huttenlocher D P, Klanderman G A, and Rucklidge W J. Comparing images using the Hausdorff distance[J]. IEEE Transactions on Pattern Analysis and Intelligence, 1993, 15(9): 850-863.

王 兵： 女，1982年生，讲师，博士生，研究方向为神经网络、模式识别等.

李盼池： 男，1969年生，教授，博士，研究方向为量子优化等.

杨冬黎： 女，1979年生，讲师，研究方向为进化计算等.

于晓红： 女，1982年生，工程师，研究方向为数据挖掘等.

Research on Cloud Process Neural Network Model and Algorithm

Wang Bing①Li Pan-chi①Yang Dong-li①Yu Xiao-hong②①(School of Computer & Information Technology, Northeast Petroleum University, Daqing 163318, China)
②(Exploration and Development Research Institute, Daqing Oilfield Company, Daqing 163712, China)

For modeling and solving problems of complex nonlinear systems whose input/output have uncertainty and are associated with time or process, a cloud process neural network model is built in the paper. It has uncertainty information processing ability by combining process neural network’s processing ability for time-varying signal with cloud model transformation ability between qualitative and quantitative concepts. In addition, the cat swarm optimization algorithm is used to optimize the network structure and parameters simultaneously, and it helps to improve network approximation and generalization performance. The effective extension of neural networks in time domain and uncertain information processing field is realized. Experimental results verify the effectiveness and feasibility of the model and algorithm.

Cloud model; Cloud process neural network; Cat swarm optimization; Time series prediction

TP183

A

1009-5896(2015)01-0110-06

10.11999/JEIT140329

2014-03-13收到，2014-06-03改回

国家自然科学基金(61170132)和中国博士后科学基金(201003405)资助课题

*通信作者：王兵 wangbing0812@sina.com