造父变星的测距功能

□ 赵君亮

造父变星的测距功能

□ 赵君亮

造父变星因其测距功能而闻名遐迩，享有“量天尺”之美誉。在天体距离测定的诸多方法中，只要造父变星之“鞭长所及”，由其周光关系所确定的天体距离往往有着最高的精度。事实上，除利用周光关系外，还可以通过其他一些途径来测定造父变星及其母星系的距离。

周光关系

1908年，美国女天文学家勒薇特（H.S.Leavitt）首次注意到在河外星系小麦哲伦星云（小麦云）中，造父变星的光变周期越长，变星的亮度越大（或者说视星等m越小），她的观测样本最初计有16颗变星。4年后，造父变星的样本数扩大到25颗，而对样本变星观测资料的分析再次证实了上述发现：变星光变周期P与变星平均视星等m之间存在简单的线性关系。鉴于小麦云的大小（约5.3kpc）远小于它的距离（58kpc），可以认为这些变星到地球的距离大致相等，由此可推知变星光变周期P与变星平均绝对星等M之间同样存在着简单的线性关系，这就是后人所称的周光关系（参见图1）。

光变周期P是可观测量，有了周光关系，便可以由周期P推知变星的平均绝对星等M。另一方面，变星的平均视星等m也是可观测量。于是只需比较m（表征亮度）和M（表征光度）的大小，便可确定变星的距离R，这是因为观测亮度m与内禀光度M成正比，又与距离R的平方成反比，即m、M、R三者有着明确的关系。这种通过恒星（或其他类别天体）的光度所推算出的距离称为光度距离。

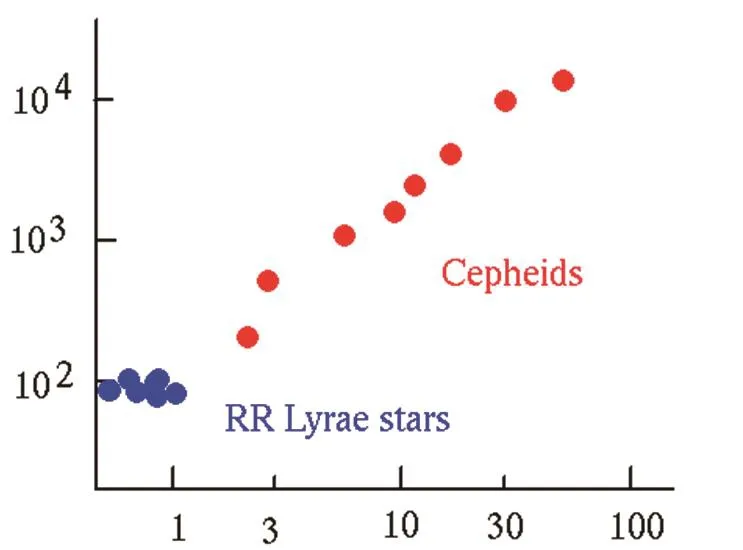
图1 造父变星（红色）周光关系示意图；横坐标为对数标度的周期P（天数），纵坐标是光度，蓝色是天琴RR型变星。

1956年，德国天文学家巴德（W.Baade）确认造父变星应分为星族I造父变星和星族II造父变星两类，它们各有不同的周光关系，两者的零点之差约为1.5mag，即对同样光变周期的星族I和星族II造父变星，前者的平均绝对星等要比后者约小（即亮）1.5mag。这一发现称为周光关系之零点改正，在周光关系研究中具有里程碑式的意义，它说明对于不同星族的造父变星，必须采用不同的周光关系，否则将会给目标天体的距离测定值较实际数值大上1倍或减小为一半，并会沿着宇宙距离阶梯进而影响到哈勃常数H0的测定值。

最著名的例子便是哈勃关于仙女星系M31距离的早期测定。哈勃用了沙普利（H.Shapley）给出的星族II造父变星周光关系，而他所观测到的M31中的造父变星则是一些星族I天体。周光关系的错误应用（当时尚无人认识到这一点），使哈勃得出的M31的距离（28.5 Mpc）比实际数值小了一半，而据此推算出的哈勃常数则大了一倍，并进而使由哈勃常数H0的倒数得出的宇宙年龄小了一半，甚至小于最年老恒星的年龄，而这是不可能的。周光关系及其正确应用对天体距离测定、以至对宇宙学研究的重要性由此可见一斑。

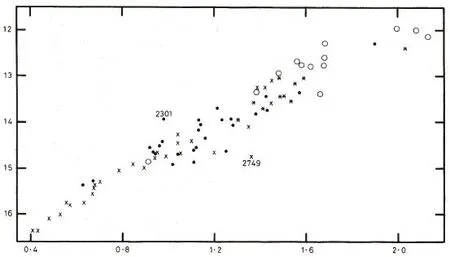
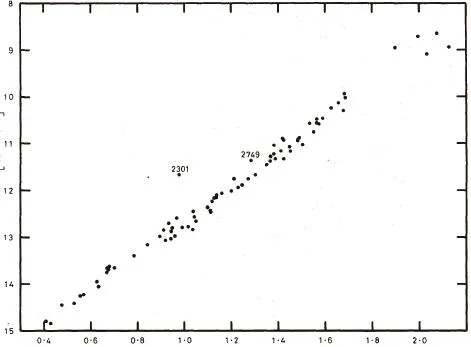
图2 大麦云造父变星之周光关系（上）和周光色关系（下）的比较；横坐标为log P。

鉴于周光关系在天体距离测定中的重要性，长期以来人们对它进行了多方面的深入探讨，如：

在周光关系中增加颜色项，引入“周光色关系”。至少对光变周期范围7.9

随着空间观测的成功实施，从早期周光关系仅限于可见光波段，拓展为多波段周光关系，并发现中红外波段的周光关系受星际消光的影响最小。

建立由极大光度Mmax取代平均光度M的周光关系，使周光关系测距的适用范围更大。这是因为距离一远，如果变星在极大光度前后尚能观测到，而其他时段观测不到，那么就无法取得变星的平均光度，只能采用极大光度表示的周光关系。

造父变星是一类高光度的脉动变星，目视波段的平均绝对星等的范围为-2>M>-6，光变周期的范围为2

鉴于周光关系对星系和宇宙学研究（包括哈勃常数确定）之重要性，为纪念勒薇特上述发现100周年，美国于2008年11月举行了一次专题讨论会。在那次会上，会议组织者提议把造父变星的周光关系改称为勒薇特定律。

图3 发现造父变星周光关系的美国女天文学家勒薇特（1868～1921）

巴德－威塞林克方法

上一节告诉我们，测定恒星光度距离是一个“三步曲”过程：

i 通过观测取得目标恒星的视星等（亮度）；

ii 利用周光关系推算出同一恒星的绝对星等（光度）；

iii 由视星等和绝对星等确定恒星的距离。

在这一过程中，关键的是第二步——设法取得目标天体的绝对星等。事实上，除了周光关系，还可以通过别的一些途径来求得天体的光度，巴德－威塞林克方法（BW方法）即是其中之一，该方法经巴德提出、并由荷兰天文学家威塞林克（A. J.Wesselink）予以完善而得此名。BW方法得出的距离也是光度距离，同样遵循上述“三步曲”过程，只是关键的第二步比周光关系来得复杂——先由恒星的颜色（或光谱形状）算出恒星的表面温度，如同时又能测得该恒星的线半径, 就可推算出恒星的光度（绝对星等）。

应用BW方法的要点是要测得恒星的线半径，而要做到这一点颇为不易。恒星实在太远了，即使在大型望远镜视场中也只是一些点光源。只有对极少数距离非常近而体积又很大的超巨星，才能通过干涉测量技术测出其角半径；或者对满足某些苛刻条件的分光双星，才有可能测定恒星的线半径，而这对确定遥远星系的距离毫无用处。

办法是人想出来的，而且办法总是比困难来得多。天文学家发现，要是恒星星体的大小会随时间发生变化，如造父变星一类的脉动变星，或者超新星之类的爆发变星，上述测定恒星线直径的难题就有可能得到解决，而这类天体便是BW测距法的用武之地。

地球上所能观测到的只是恒星的表面大气层。如果恒星在膨胀（或缩小），恒星的观测视向速度（恒星运动速度在观测者视线方向上的分量）就是两项速度的合成：一是恒星本体空间运动速度的视向分量，二是恒星大气层相对恒星本体之运动速度的视向分量。只要在一段时间内不断监测恒星视向速度的变化，得到不同时刻恒星大气膨胀（或收缩）的速度，就可以设法推算出恒星的线半径。

在用BW方法测定变星光度距离时，一个重要问题是观测资料的同时性。该方法需要对目标恒星进行测光和光谱观测，前者用于得到恒星视星等，而后者用以测定恒星的视向速度，并进而推算其线半径和绝对星等。现在的观测对象是变星，它们的视星等、线半径和绝对星等都随时间而变化。要能确定变星的光度距离，原始测光资料和光谱资料必须在同一时间取得。严格做到观测资料的同时性显然是有一定困难的，而这就会影响到距离测定的精度。同样是造父变星，由周光关系来测定其光度距离时，并不存在这类同时性要求。

BW方法的最大测距范围约为1Mpc，远小于周光关系的适用范围。

回光测距

就物理本质而言，光度距离是通过比较天体的亮度（视星等）和光度（绝对星等）而推得的距离。类似地，如能测得天体的角直径，同时又测出其线直径，那么也可推算出天体的距离（参见图4）,由此测得的距离称为尺度距离或角径距离。这一基本思想为天体距离测定提供了一条独立的途径。不过，由于天体角直径和线直径的精确测定都十分困难，对于遥远的天体来说，尺度距离仅能在少数特定的情况下具有实用价值。

在星系内，除大量恒星外，还广泛分布有星际介质，星际介质密度相对较高（气体和尘埃的数密度大于101～103质点/厘米3）的地方便构成弥漫状的气体尘埃云，即星云，星云和星云之间的云际物质平均密度仅约为0.1质点/厘米3。如果星云内部或附近有一颗或若干颗温度并不太高（光谱型通常晚于B1型）的明亮恒星，星云会因反射恒星的星光而发光，这就是反射星云。借助回声的概念，由星云所反射，并为我们观测到的星光亦可称恒星回光（light echo）。

图4 远方一颗恒星在观测者O处的张角为θ，而恒星的线直径为d。由这两个量可得出恒星的距离R= d/ θ，称为尺度距离。

众所周知，回声可用以测距：如果你在一个寂静的山谷中朝着远处的峭壁大声呼叫，那么过一段时间你就会听到来自峭壁的、你自己所发出声音的回声。利用回声和呼叫声间的时间差（时间延迟）便可估测出你到峭壁的距离，这就是回声测距。回声是一种声学现象，而回光则是一种光学现象。

那么，什么是回光测距？

如果有一颗造父变星深埋于气体尘埃云之内，云块表现为反射星云，那么随着变星光度的周期性变化，星云的反射光（回光）强度也会发生相应的规则变化。对于地球上的观测者而言，先观测到的是变星直接发出的星光，然后才是经星云反射过来的回光，回光较之星光在时间上则有所延迟。利用这种回光现象的这种时间延迟效应，可以推算出造父变星及其母星系的尺度距离。

星云回光强度的变化会从最靠近变星的区域，朝着远离变星的区域，以光速向外传递。经过一段时间后，在恒星周围的一定范围内便可观测到若干个亮度为极大的“特征结构”。不过，由于云块内物质密度的分布并不均匀，能看到的只是一些亮斑点（或短光弧），因为那儿的物质密度高，回光较强而易于观测到。只要能取得这些特征光斑到变星本体的线距离和角距离，便可以确定变星的尺度距离，这就是回光测距的基本原理。

图5 船尾RS及其周围反射星云中的4个回光光班。

回光现象较为罕见，回光测距对观测资料有着特定的要求，且必须有足够高的空间分辨率，迄今尚未取得广泛应用，测距较为成功的仅见于造父变星船尾RS（参见图5）。这是一颗非常明亮的经典造父变星，光变周期为41.384天。1972年，有人利用该变星周围反射星云中3个特征光斑，得出该变星的距离为1.78kpc，这一结果与变星光度距离的测定值符合得相当好（由周光关系测得的该变星的光度距离为1.83kpc）。

天琴RR型变星作为标准烛光

如造父变星那样能用来测定距离的天体称为标距天体，它们可以是恒星，也可以是其他类别的天体；而像周光关系那样可用以推算距离的关系式称为标距关系。

要是能证实某一类恒星的光度（绝对星等）是恒定的，或仅有少量变化，且与其位于何处无关，那么对于未知距离的远处同类恒星,只要测得其亮度（视星等），便可利用它们的已知绝对星等来推算出目标天体的距离。这种有恒定光度的标距天体又可称为标准烛光，所测得的距离也属于光度距离。

天琴RR型变星亦称短周期造父变星，光变周期约为0.05～1.5天，光变幅度一般不超过1～2个星等，因其原型恒星天琴RR而得名。观测研究表明，不同天琴RR型变星最亮绝对星等的差异不超过1个星等，平均值约为0.6等, 且这一数值与光变周期没有太大关系（参见图1中的蓝点）。这就是说, 只要是天琴RR型变星，无论其光变周期多大，极大亮度时的绝对星等都约为0.6等，这就为天体距离测定提供了一种标准烛光。尽管用这种标准烛光得出的光度距离之误差比较大，但在同一个星系中此类变星为数众多，可综合利用以减小母星系距离测定值的统计误差。例如，利用天琴RR型变星作为标距天体测得的M31之光度距离为750kpc，与由周光关系得出的结果760kpc符合得很好。

地面望远镜所能观测到的、天琴RR 型变星的最远距离约为250kpc，利用哈勃空间望远镜可测得的该类变星的最远距离约为1Mpc，与BW方法的测距范围差不多，尚不超出本星系群的范围。

在上述4种测距方法中，以周光关系和天琴RR型变星作为标准烛光的应用最为广泛，尤以前者的适用范围远大于其余3种方法。尽管经典造父变星是一类高光度恒星，但在BW方法中需要取得变星的光谱，这就大大限制了可测变星的距离范围。对于回光测距法，不仅要测得变星本体的光变曲线，还需取得回光光斑的光变特征，因为光斑的亮度总是要比变星自身的亮度小得多，这同样会使可测变星的距离范围大受限制。

（责任编辑 张长喜）