一题多解使学习数学事半功倍

广东省肇庆市德庆县香山中学 李素琼

题目：7人排队，其中甲乙丙3人顺序一定共有多少不同的排法？

方法一：倍缩法。

对于某几个元素顺序一定的排列问题，可先把这几个元素与其他元素一起进行排列，然后用总排列数除以这几个元素之间的全排列数，则共有不同排法种数是：

方法二：空位法。

设想有7把椅子让除甲乙丙以外的四人就坐共有种方法，其余的三个位置甲乙丙共有1种坐法，则共有种方法。

方法三：插入法。

可以先让甲乙丙就坐，先排甲乙丙三个人，共有1种排法，再把其余4四人依次插入共有方法。

排列组合历来是学习中的难点，排列组合问题联系实际生动有趣，但题型多样，思路灵活，解决排列组合问题，首先要认真审题，弄清楚是排列问题、组合问题还是排列与组合综合问题；其次要抓住问题的本质特征，采用合理恰当的方法来处理。通过我们平时做的练习题，不难发现排列组合题的特点是条件隐晦、不易挖掘、题目多变、解法独特、数字庞大、难以验证。对有关排列组合的几种常见的解题策略加以复习巩固，只有对基本的解题策略熟练掌握，根据它们的条件，我们就可以选取不同的技巧来解决问题。对于一些比较复杂的问题，我们可以将几种策略结合起来应用把复杂的问题简单化，举一反三，触类旁通，进而为后续学习打下坚实的基础。

通过本例的证明与拓展，学生掌握了相关的知识与技能，体会到知识的联系与综合，通过一题多解是从不同的角度、不同的方位审视分析同一题中的数量关系，用不同解法求得相同结果的思维过程。因此，我们总结了在实际教学中一题多解有以下几点的作用。

第一，一题多解有利于培养学生思维的广阔性。

对于同一道题，从不同的角度去分析研究，可能会得到不同的启示，从而引出多种不同的解法。在教学中，不失时机地通过引导学生进行“一题多解”的训练，通过广泛的联想，使我们的思维触角伸向不同的方向，不同的层次，这样不仅能巩固所学知识，而且能较好地培养学生思维的广阔性。转化思想在数学中的地位非常重要，同时要求学生认真比较三种解法的利弊与依据，然后启发学生：一道好题能激发人的兴趣，引导人的思想，启迪人的思维，在平时的学习中应养成探索不同的方法解题的习惯，这样才能更好地提高解题的能力。

通过一题多解，既能促使学生沟通知识点间的联系，又培养了学生的思维能力。同时也让学生通过对比、小结，得出自己的体会，充分发掘自身的潜能，从而提高自己的解题能力，这不仅引导学生多方法，多视角思考问题和发现问题，形成良好的思维品质，而且使学生感受到成功的喜悦和增强自信心，也极大地激发学生学习数学的积极性和浓厚的兴趣，从而在很大程度上培养了学生思维的广阔性。

第二，一题多解有利于培养学生思维的深刻性。 思维的深刻性，不仅表现在审题时能很快发现和抓住问题的基本特征，挖掘出隐含条件，从而迅速确立解题的策略，而且还表现在解题后不满足于“一题一法”而是深刻领会解题的实质，掌握其一般规律。一般要通过挖掘隐含条件，更简洁更准确的给出解答，通过对比可知分析题目时，不能老把思维停留在题目的表面上，而要深入洞察问题的实质，揭示问题中的本质特征，从而养成深刻思维的良好习惯，达到优化解题的效果。

第三，一题多解有利于培养学生思维的灵活性。

数学问题形式多样，千姿百态，由于思维定势产生的负效应，学生解题时往往墨守成规，故思维灵活性的培养在解题教学中，主要表现为一题多解。即善于根据题设中的具体情况，及时地提出新的设想和解题方案，不固执己见，不拘泥于陈旧的方案。

第四，一题多解有利于培养学生的创新思维。

一题多解对学生创新思维能力培养起着重要的作用。一题多解的训练，可开拓学生思路，提高学生思维的灵活性和敏捷性；在培养学生创造思维能力方面有特殊的功能；也是发展学生创造力的主要途径之一。

习题：已知为等差数列，其前10项的和S10=100，前100项的和S100=10。求前110项的和S110。

方法一：要求等差数列的和可先求首项及公差，利用方程思想(常规解法)

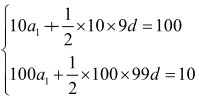
方法二：函数思想（待定系数法）

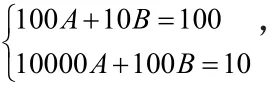
再由S =A × 1 102+B × 1 10 = -110

因为数列{an}为等差数列

方法三：利用性质（简化运算）

因为数列{an}为等差数列，

通过此题采用多种解法解答不但激发了学生的创新思维，也培养学生的创造性思维；使学生能够全面发展成为拥有良好的创新思维品质和勇于探索的科学精神的高素质人才。

总之，一题多解是数学题解教学中的一种常用方法，是培养、提高学生思维能力，创新能力，分析问题解决问题能力的有效方法。只要我们能善于运用，积极引导学生运用，就能培养学生创新能力和创造性的思维能力，而且也能减轻学生学习数学的负担，还能提高学生学习数学的效率，从而增强学生学习数学的兴趣，真正发挥一题多解在中学数学教学中应有的作用。教学中适当的一题多解，可以激发学生去发现和去创造的强烈欲望，加深学生对所学知识的深刻理解，训练学生对数学思想和数学方法的娴熟运用，锻炼学生思维的广阔性和深刻性、灵活性和独创性，从而培养学生的思维品质，发展学生的创造性思维。