基于最小二乘法的地铁盾构隧道结构横断面测量方法研究

高帅(北京城建勘测设计研究院有限责任公司,北京 100101)

基于最小二乘法的地铁盾构隧道结构横断面测量方法研究

高帅
(北京城建勘测设计研究院有限责任公司,北京 100101)

摘 要:基于既能加快内、外业作业进度,又能满足现实测量工作条件的目的,文中以合肥某盾构隧道结构横断面实际测量作业为背景,提出了一种利用全站仪结合最小二乘空间拟合的方法对盾构隧道结构横断面测量数据进行处理。通过将该方法处理获得的数据与实际测量值进行比较,结果显示采用该方法对地铁盾构隧道结构横断面测量数据进行处理是可行且准确的。同时,在保证一定数目的测量点参与拟合计算的前提下,该方法可在一定程度上降低测量环境对工作的制约,使得工作效率大大提高。

关键词:最小二乘法;盾构隧道;横断面测量

1 引 言

随着城市现代化水平的不断提高,地下轨道交通工程呈现快速发展的趋势。盾构法施工技术以其对环境影响小、施工效率高、适用范围广等优点,在国内得到了广泛的应用。盾构隧道贯通后,大量的隧道结构横断面测量工作成为困扰测量工程师的问题,如何快速处理大量的断面测量数据,同时避免出错,成为测量工程师的一个新挑战。

城市轨道交通工程盾构隧道结构横断面测量,是验证土建施工后限界尺寸和有效净空能否满足设计要求所进行的测量工作,其测量精度要求高、施测密度大,虽然施测方法多种多样,但都有其自身的缺点和局限性。因此,寻求一种既能加快内、外业工作的作业进度,又能满足现实测量工作条件的方法,具有很强的现实意义。本文以我院在合肥城市轨道交通工程盾构隧道结构横断面测量工作的实际测量作业为背景,提出了一种利用全站仪结合最小二乘空间拟合的方法对盾构隧道结构横断面进行测量及数据处理的测量方法。

2 盾构隧道结构横断面测量的一般要求

城市轨道交通工程盾构隧道结构横断面测量主要是在铺轨前,以归化改正后的线路中线点或贯通平差后的施工控制点为依据,采用与原施工图相一致的坐标和高程系统、图式所进行的测量工作。按照设计和工程实际需要,一般情况下,直线段每6 m、曲线段每5 m测量一个横断面。曲线段各线路要素点处、联络通道、车站起点、终点等断面突变处以及施工偏差较大段须按管片逐环测量横断面。

盾构隧道结构横断面测量,可采用Ⅲ级全站仪、断面仪等进行。测量断面点的里程允许误差应在±50 mm之内,断面点与线路中线法距的测量中误差为±10 mm,断面点高程的测量中误差为±20 mm。测量的横断面方向必须在设计线路中心线的法线上,误差小于±5′。

按照设计提出的要求,盾构隧道结构横断面(含盾构起点钢环)测量内容如图1所示,A、B、S、D、H等测量成果需要整理成设计需要的电子版表格形式。

图1　盾构隧道结构横断面测量示意图

3 基于最小二乘法的拟合模型

3．1空间平面拟合

按照已有理论,我们以盾构隧道结构横断面所在的平面与球体相交形成的圆方程组作为基础方程进行求解,可以拟合出盾构隧道结构横断面的三维空间圆的圆心点坐标,将每个圆心点连起来即为盾构隧道设计线路中心线。

假设盾构隧道结构横断面圆心点的三维坐标为(x0,y0,z0),半径为r。断面上均匀分布n个三维坐标测量点,且坐标为(xi,yi,zi),i=1,2,…,n。为了计算方便,不考虑盾构隧道结构横断面所在的空间平面通过坐标原点的情况,则它的平面方程可以表示为:

将观测值代入式(1)中可以得到:

其中,L=[1…1]T,X = [a,b,c]T。根据最小二乘法VTQV = min可以得到平面方程的最小二乘解X = (BTQB)-1BTQL,其中权阵Q可以取单位矩阵或根据实测坐标合理取值。

由于盾构隧道结构横断面在实际测量时并不是完全垂直于地面的,因此还要计算出空间平面和水平面之间的二面角作为盾构隧道结构横断面测量的质量评价指标。

假设拟合平面的法向量为→i1(a,b,c),水平面法向量为→i2(0,0,1),二面角为θ,则有:

3．2空间圆拟合

空间圆实际就是空间圆球体与空间平面的交点所形成的圆形,本文采用带约束条件平差方法求解空间圆形。空间圆球体的方程可以表示为:

待求参数的初始值计算方法为:

将观测值代入式(4)并展开可得到误差方程:

条件方程C^x-Wx=0即为平面拟合方程axi+byi+ czi=1。联立误差方程和条件方程可得新函数:根据附有条件的间接平差方法可以得到法方程:

解算法方程得到待解参数的改正数,迭代计算可以得到圆心坐标(a0,b0,c0)及半径r。

4 精度评价

平面拟合的残差可以用各实测点到拟合平面的距离来表示,其计算方法为:

拟合圆的残差可以用各点到圆心距离与半径的差值来表示,其计算方法为:(10)

每个实测三维坐标点在圆心拟合计算时的总体残差可以表示为:则最后得到的观测中误差为:

5 工程实例验证

为了验证通过最小二乘法空间拟合来对盾构隧道结构横断面测量数据进行处理方法的可行性,本文选取合肥地铁一号线某盾构区间隧道作为工程实例,将实际测量点位数据进行空间拟合获得的圆心坐标数据与设计值进行了比较,结果显示该方法是可行且准确的。实际测量过程中,空间测量点均匀地布设在管片拼接缝的大里程端。实测的空间测量点三维坐标数据如表1所示,点位空间分布图如图2所示,均匀分布在结构横断面上。

对表1中的观测数据采用上述算法进行空间拟合计算,可以得到各个测量点拟合的残差值、结构横断面拟合圆心坐标值。经计算,该结构横断面拟合圆心为(3517096．396,27007．969,7．763),半径为2．698 m,结构横断面所在平面与水平面的二面角为90°03′31．24″,观测中误差为±0．65 cm。各个测量点拟合的残差值如表2所示。

图2　测量点位分布示意图

空间测量点三维坐标数据 表1

测量点空间拟合残差值 表2

8号点的拟合残差值过大,为了提高拟合的精度,在空间拟合计算圆心坐标的过程中需要将该点位剔除,剔除8号点之后其余点拟合得到圆心坐标数据,并将结果与传统方法测量值进行比较,如表3所示。经比较,拟合处理结果可以用于分析计算盾构隧道结构横断面的限界值。

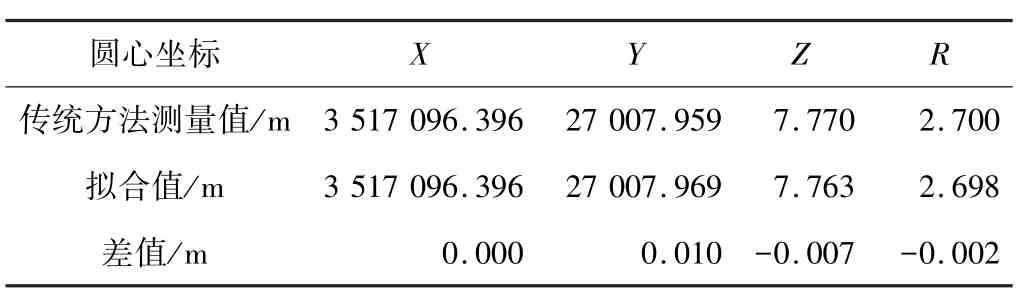
空间圆拟合圆心与传统方法测量值比较结果 表3

为验证依据该方法计算得到的各限界检测值的可靠性,分别直接测量各值并进行比较,结果如表4所示,可见结果满足要求,方法可行。

拟合计算值与直接测量值比较结果 表4

6 结 论

本文对基于最小二乘法的空间拟合技术在盾构隧道结构横断面测量中的应用进行了研究,提出了该技术在盾构隧道结构横断面测量中的数据获取和数据处理方法。经已有工程进行实例验证,得到如下结论:

(1)通过该方法计算获得的盾构隧道结构横断面圆心坐标数据与传统方法测量值之间的差值满足工程要求的精度,该方法具有可行性和科学性。

(2)为保证拟合结果的精度,空间拟合计算的过程中,应该保证足够多的点参与计算。

(3)在外业测量的过程中应使测量点尽量均匀地分布在结构横断面上,在拟合计算的过程中应将残差较大的点位剔除,但是顶部和底部的点不能被剔除,否则需重测该横断面。

(4)将原理公式程序化之后,可以实现对盾构隧道结构横断面数据的批量处理,使得测量工作的效率大大提高。

参考文献

[1] 武汉大学测绘学院测量平差学科组．误差理论与测量平差基础[M]．武汉:武汉大学出版社,2003．

[2] 陶本藻．测量数据处理的统计理论和方法[M]．北京:测绘出版社,2007．

[3] 陈大勇．地铁盾构隧道洞门圈中心坐标测量与数据处理方法的探讨[J]．城市勘测,2008(2):86～89．

[4] 王思锴．城市轨道交通工程隧道结构断面测量技术方法的实践与探索[J]．城市勘测,2011(1):130～132．

[5] 王荣权．轨道交通工程隧道结构断面测量技术与方法[J]．铁道勘察,2008,34(1)17～19．

[6] 贺磊,韩旭,陆晓勇．地铁盾构隧道断面测量数据的处理研究[J]．测绘通报,2015(6):79～81．

[7] 蒋勇．城市轨道交通调线调坡测量中圆隧道横断面测量方法的探讨[J]．城市勘测,2011(2):142～144．

[8] 高俊强,陶建岳．利用免棱镜全站仪进行地铁隧道断面测量与计算[J]．测绘通报,2005(10):41～43．

The study of Cross-section Surveying Method Which is Based on Least Square Method in Metro Shield Tunnel

Gao Shuai
(Beijing Urban Construction Exploration & Surveying Design Research Institute Co．,Ltd,Beijing 100101,China)

Abstract:The paper takes the shield tunnel cross-section measurement of actual operatic in Hefei urban rail transit construction as the background, it puts forward a method of measurement data processing which combines the total station and least square method．Compared with the design results, the calculated results by the least square method is feasible and accurate．At the same time, it reduces the influences of measurement environment on the survey work to some extent and it makes the work efficiency is greatly increased under the premise that ensure there is a sufficient number of measurement point in fitting calculation．

Key words:least square method;shield tunnel;cross-section survey

文章编号:1672-8262(2015)06-94-04中图分类号:P258

文献标识码:B

收稿日期:∗2015—09—21

作者简介:高帅(1987—),男,硕士,助理工程师,主要从事城市轨道交通工程测量工作。∗