在轨拦截器最短拦截路径选择方法
仉小博,谭 飞,朱 昱,冯博鑫,曹 锐
(1.第二炮兵工程大学906 室,西安 710025;2.第二炮兵装备部 西安军事代表处,西安 710025;3.中国人民解放军96167 部队,福建 永安 366000)
近年来,由美国主导的几场高技术局部战争的结果表明,空间信息网络已成为现代战争中决定胜负的重要因素之一。显然,在战争条件下如果一方空间信息网络被破坏或摧毁,将直接影响到该方战争的胜负。这说明其空间力量越强大,在战争中,战场对空间信息网络的依赖性就越强。因此,如果能有足够的能力,在战争条件下将敌方空间信息网络进行有效破坏或摧毁,就可导致敌方战场处于瘫痪状态,而这一信息网络的重要组成部分就是空间卫星。所以,各军事大国不仅都在竞相发展空间技术,同时也在大力发展反卫拦截技术。拦截技术的发展,必然引发反拦截技术的研究,本文就是基于反拦截条件下,对拦截器的拦截轨道进行选择与优化的方法进行探讨,以便提高拦截器的突防概率。
1 空间拦截环境分析
1)拦截器与目标卫星空间运动状态分析。在轨拦截器与目标卫星均在空间预定轨道上运行,显然二者的轨道参数均为已知。二者都是在地球引力场的作用下运动,运行轨道与地球间的空间几何关系及运动参数均可推出。
2)反拦截系统布局与状态分析[1]。本文只考虑上升式反拦截器对空间拦截器的拦截与威胁。由于上升式反拦截器其拦截范围只能是其发射阵地上方空间的某一区域,可以近似为圆锥体,如图1 所示。区域大小是由该阵地反拦截的空间最大机动范围确定,可以通过弹道仿真获得。
3)空间拦截路径规划要求条件限制。选定的拦截路径必须满足以下要求[2]:突防概率要求,选定的最佳拦截路径能够使拦截器的突防概率最大。拦截器性能要求,路径选择必须满足拦截器的能量限制和机动能力约束。战略与战术要求,路径规划必须要做到反应迅速、规划周期短、适应性强,以应对战争中可能会出现的特殊情况。
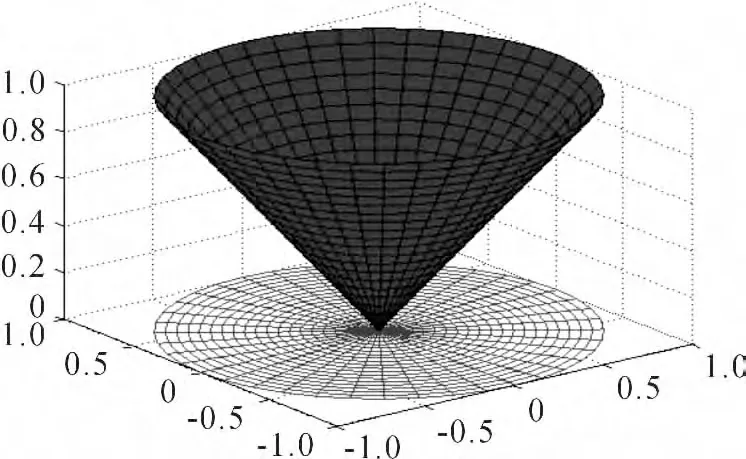
图1 单个发射阵地空间防御区域示意图
2 基于突防概率要求的空间最佳拦截路径选择与优化
对于拦截器拦截路径规划问题,目前应用的主要方法有动态规划方法、最速下降方法、专家系统法和遗传算法等[3-4]。以下主要研究空间拦截点一定的条件下,如何确保空间拦截突防概率最大时,其空间拦截最佳路径的规划问题。
2.1 突防策略分析
最佳突防策略就是确定一条拦截轨道,使拦截器在对卫星实施拦截时,在反拦截的条件下其突防概率最大[5]。由于拦截器与目标卫星的运行轨道和运动规律均为已知,所以在给定拦截时间的前提下,可以确定拦截器对卫星实施拦截时的拦截点位置和反拦截器的空间最大防御区域,拦截点的具体位置有两种情况:一是拦截点不在最大防御区域内,显然拦截路径可以随意选取;二是拦截点在最大防御区域内,这时我们根据路径最短,突防概率最大的原则,选择一条最短路线作为最佳拦截路径。而本文主要研究拦截点在防御区域内时,如何选择最佳拦截路径的问题。
2.2 反拦截器空间防御区域确定
存在多个反拦截器发射阵地的情况下,以3 个防御阵地为例,其空间防御区域如图2 所示。
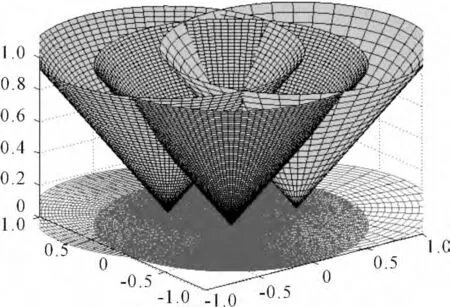
图2 多个发射阵地的空间防御区域示意图
2.3 拦截器最佳拦截路径规划与建模
不考虑其他因素影响,选取最短路径作为最佳拦截路径。将2.2 确定的空间防御区域投影到地面则最大防御区域可以看做由一个或多个圆形区域交叉覆盖形成的一个大的防御区域,如图3 所示。假设拦截器拦截卫星时的拦截点投影到地面为P 点。由以上空间拦截环境分析可知,在轨拦截器最佳拦截路径规划问题可以抽象为以下数学模型:已知平面坐标下任意多边形S(由所有发射阵地的中心点坐标和其在空间的最大机动范围确定)以及该多边形内任意一点P(xP,yP)的坐标,求出多边形上一点T(xT,yT),将这一点称为进入点,使得进入点T 到拦截点P 的距离
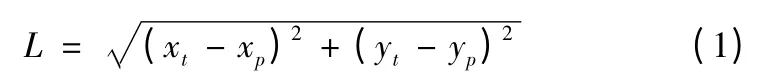
最小,即要求出min L,以及对应的点T(xT,yT)如图3所示。
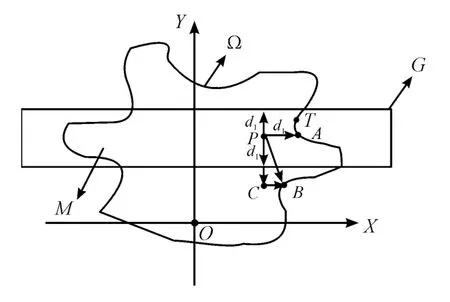
图3 简化模型分析示意图
3 算法设计与仿真
3.1 算法设计
经过对以上所建立的模型分析,要求出多边形Ω 上一点T (xT,yT),使 得 T 点 到 P 点 的 距 离 L =最小,为了能够获得min L,必须遍历多边形Ω 上的所有点,得到一系列Li,最后取L=min(L1,L1,…,Ln),其计算流程如图4 所示。
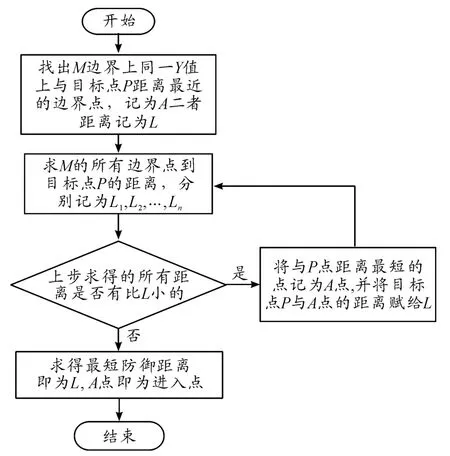
图4 最佳拦截路径确定流程
计算步骤:
步骤1:定义平面直角坐标系XOY,原点为多边形Ω 内任意一点O,取正北方向为Y 轴的正向,X 轴与其构成右手直角坐标系。取Ω 上所有与P(xP,yP)点同一Y 值的点,求出这些点中到P(xP,yP)点距离最短的一点记为A1(xA1,yA1),二者距离记为d1=,将d1赋给L。
步骤2:以P(xP,yP)点为中心,2 倍d1为宽,多边形Ω 的最大长度为长,做平行于X 轴的矩形G,矩形G 与多边形Ω相交区域为M,则所要求的T(xT,yT)点必定在区域M 内。结论证明如下:如图3 所示,假设该点不在二者相交的区域M 内,可考虑M 外一点B(xB,yB)为距离P(xP,yP)最近的一点,则根据直角三角形三边关系PB >PC,但由于B(xB,yB)点是M 外一点,所以PC >d1,所以可以有PB >d1,与假设不符,所以离P 点最近的点肯定在区域M 之内。
步骤3:选取搜索步长d,矩形G 的上下边界同时减去d,求出当前Y 值对应的边界点中距离P(xP,yP)最短的点记A2(xA2,yA2),距离为d2,将d2赋给L。
步骤4:以2 倍d2为无限长矩形的宽,P(xP,yP)为中心画出无限长矩形与该多边形相交,重复步骤3,直至在相交区域找不到一点,其距离小于上一步的Ai(xAi,yAi)到P(xP,yP)的距离,则P 到Ai的距离即为P(xP,yP)点到Ω 边界的最短距离,点Ai(xAi,yAi)即为所求的点T(xT,yT),且minL =
步骤5:步骤4 中求出的进入点T(xT,yT)只是进入点在地面的投影点坐标,要最终确定进入点具体位置,还需要确定进入点距地面的高度。由于本文所建模型主要是讨论平面坐标下的拦截路径规划问题,所以将进入点距地面的高度近似为拦截点处目标卫星距地面的高度。这样就能确定出进入T 在空间的具体位置。由于缺乏目标卫星的实际轨道参数,为便于计算,下面仿真实例中的进入点T 只给出其在平面坐标下的投影点的坐标。
算法优点在于:该方法相比枚举法可以大大减少计算量;矩形G 的边界是采用上下边界同时减小,且其上下边界距离的变化率大于步长的变化率,所以效率很高。
3.2 仿真实例
根据以上设计的算法,经过编程实现,我们得到如下仿真实验结果:给定3 个防御阵地的中心点坐标及其对应的防御半径,给定拦截点坐标,利用程序进行仿真实例分析,得到进入点位置和最短防御距离。图5 表示4 组仿真实例对应的最大防御区域示例图,表1、表2 分别表示步长为0.1 km和1 km 时所求得的进入点和最短拦截距离。
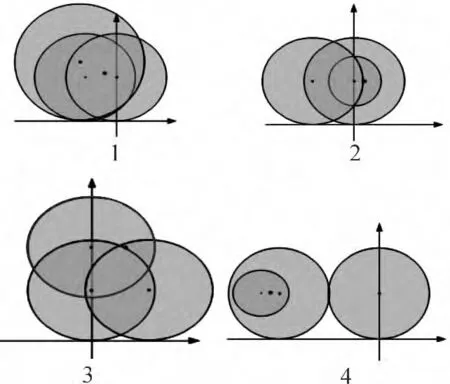
图5 最大防御区域示例
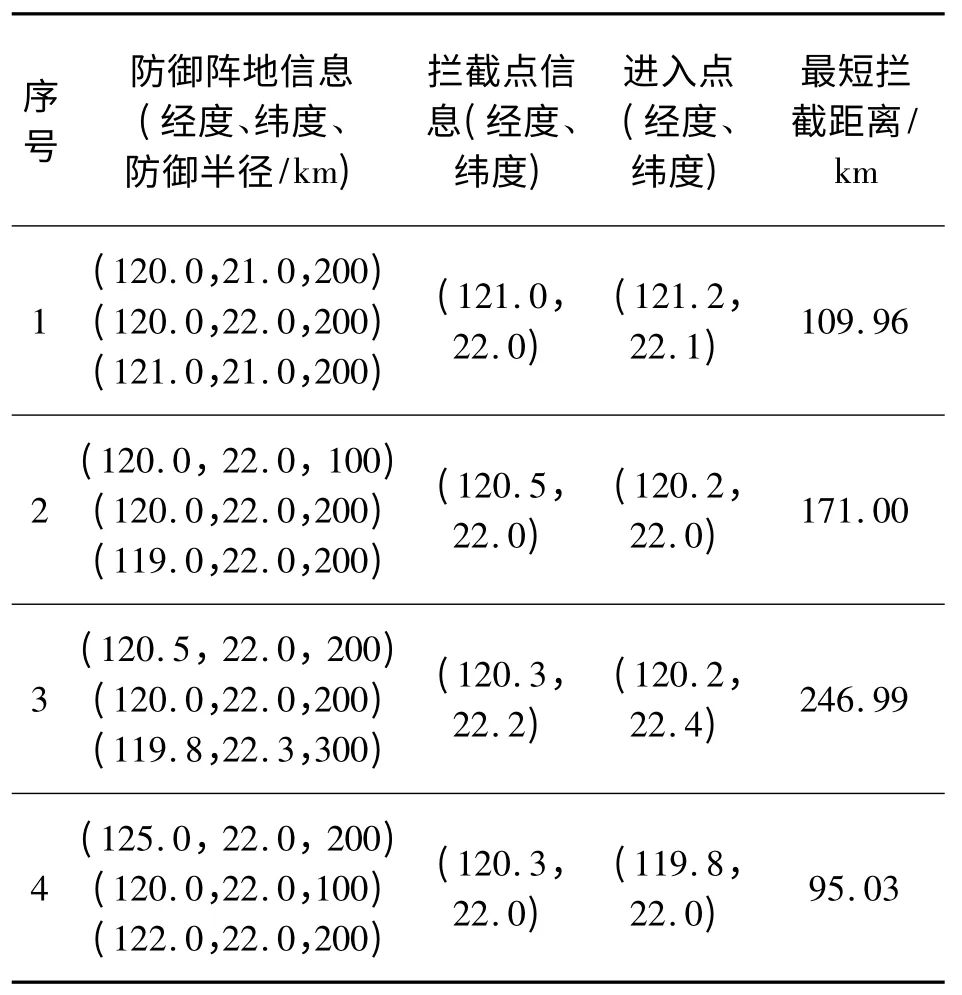
表1 步长为0.1 km 时,进入点和最短拦截距离
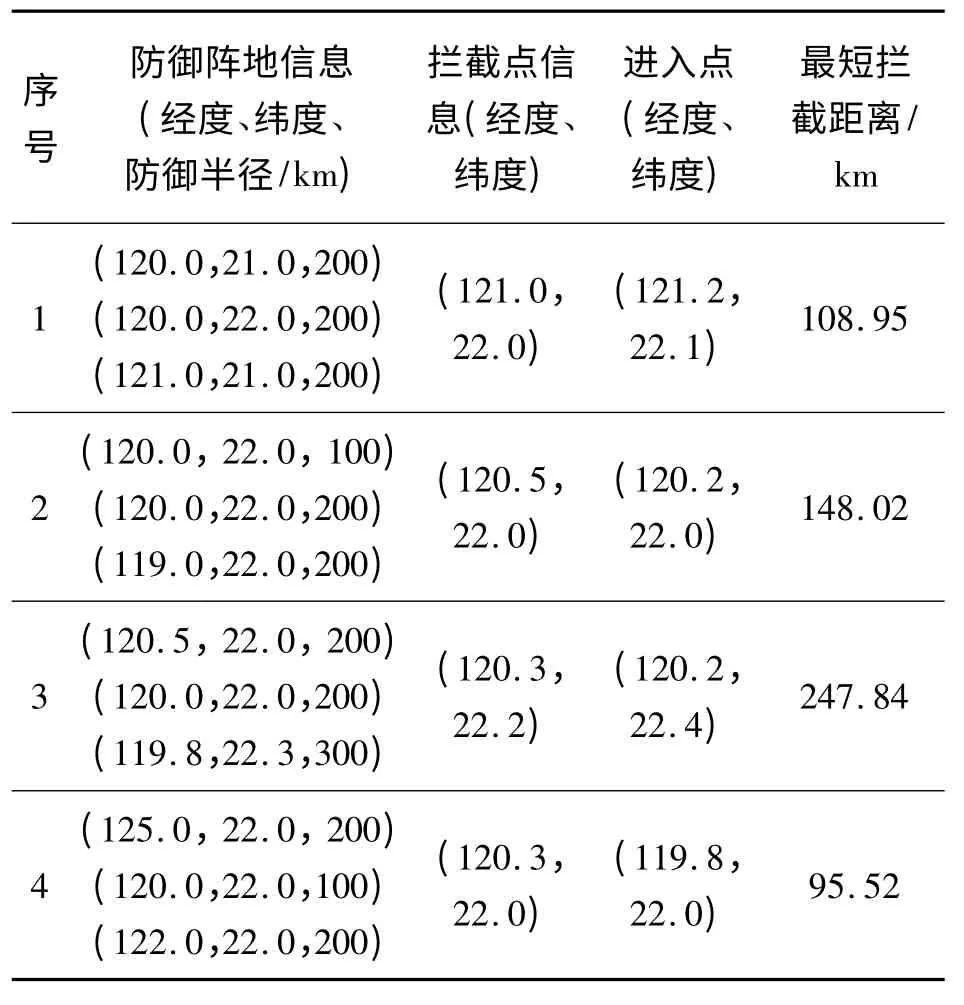
表2 步长为1 km 时,进入点和最短拦截距离
4 仿真结果分析
由表1 与表2 的结果对比可知,在相同防御区域、同一拦截点的情况下,分别选取0.1 km 和1 km 为搜索步长时,求解得到的最短拦截距离与选取的步长大小没有直接关系。考虑在轨拦截器的飞行速度快、时间短等特点,在实际操作过程中拟选取步长为1 km,其精度可以满足作战需求。
5 结束语
由仿真实验结果分析知,本文所建最佳拦截路径规划模型是合理的,所运用的算法与传统的枚举算法相比,收敛速度快,计算速度大大提高,所选取的最佳拦截路径能够有效缩短拦截器在防御区域内的拦截距离,提高突防概率。其研究结果对空间作战的理论研究具有一定的参考价值。
[1]Shinar J,Tabak R.New results in optimal missile avoidance analysis[J]. Guidance Control And Dynamics,1994,17(5):897-902.
[2]David G Hull.Conversion of optimal control problems in to parameter optimization problems[J]. Jornal of Gidance,Control And Dynamic,1997,20(1):57-60.
[3]雍恩米.弹道导弹中段机动突防制导问题的仿真研究[J].导弹与航天运载技术,2005,5(1):12-13.
[4]张光澄.最优控制计算方法[M].成都:成都科技大学出版社,1991.
[5]吴瑞林等 弹道导弹机动突防研究[J].863 先进防御技术通讯,2001(8):12-29.

