基于遗传算法和偏最小二乘法的土壤激光诱导击穿光谱定量分析研究

邹孝恒 郝中骐 易荣兴 郭连波 沈萌 李祥友王泽敏 曾晓雁 陆永枫

(华中科技大学武汉光电国家实验室(筹),激光与太赫兹功能实验室,武汉 430074)

基于遗传算法和偏最小二乘法的土壤激光诱导击穿光谱定量分析研究

邹孝恒 郝中骐 易荣兴 郭连波 沈萌 李祥友*王泽敏 曾晓雁 陆永枫

(华中科技大学武汉光电国家实验室(筹),激光与太赫兹功能实验室,武汉 430074)

在空气环境下,采用激光诱导击穿光谱(LIBS)技术对土壤成分进行检测,建立了基于遗传算法(GA)和偏最小二乘法(PLS)的定量分析模型。将配制的58个土壤样品分为定标集、监控集和预测集,对11种组分Mn,Cr,Cu,Pb,Ba,Al2O3,CaO,Fe2O3,MgO,Na2O和K2O的含量分别进行预测。结果表明, GA作为一种谱线选择的预处理方法,可以有效减少用于PLS建模的光谱谱线的数目,从而简化模型。对于土壤中的大部分组成成分,GA-PLS模型能够显著改善传统PLS模型的预测能力。以Mn元素为例,浓度预测均方根误差(RMSEP)从0.0215%降低至0.0167%,平均百分比误差(MPE)从8.10%降低至5.20%。本研究为进一步提高土壤的LIBS定量分析准确度提供了方法参考。

激光诱导击穿光谱;遗传算法;偏最小二乘法;土壤

1 引 言

激光诱导击穿光谱(LIBS)技术是一种基于激光与物质相互作用的等离子体光谱物质组分分析技术,它具有检测速度快、无需样品预处理、可进行实时在线及远程测量等优点[1],在地质分析、生物医学、环境监测和文物鉴定等领域已得到广泛研究和应用[2,3]。LIBS技术通过获取等离子体发射谱线的强度信息确定元素的含量。传统的定量分析方法包括基本定标法和内定标法[4],这些单变量模型仅利用待测元素的单条特征谱线进行定量分析,无法消除谱线干扰、自吸收效应和基体效应等因素的影响,因而准确度不能满足实际应用的需要。

偏最小二乘法(PLS)是一种多元统计数据分析方法,已用于铝合金[5]、钢铁[6]、煤炭[7]和植物[8]等材料的LIBS成分检测。PLS利用一段光谱或全谱的所有数据点作为自变量,分析元素浓度作为因变量,拟合光谱强度和元素浓度之间的关系,在一定程度上可以克服传统单变量模型的缺陷。但由于这些变量通常会包括一些与浓度相关性较弱,甚至完全不相关的信号,因此会降低PLS模型定量分析的真实性和准确度。通过对LIBS的原始光谱数据进行预处理,去除与分析元素浓度无关的噪声信号,保留相关信息,可以提高PLS的预测精度。遗传算法(GA)是一种有效的全局优化算法[9],它借鉴生物界的自然选择和遗传机制,利用选择、交叉和变异等操作,以给定的优化标准对光谱谱线进行筛选。GA与PLS结合(GA-PLS)用于物质成分分析的优越性已经在近红外光谱中得到证实[10～13]。然而,在LIBS领域应用较少。Fink等[14]将GA-PLS应用于LIBS,对热塑料中的Ti元素进行定量分析,与传统的PLS方法相比,光谱输入变量数目从87减小到22,定标均方根误差(RMSEC)和交互检验均方根误差均显著下降。Gottfried等[15]将GA-PLS与LIBS结合,并应用于碳酸盐、氟石和硅酸盐地质材料的分类中,用GA提取部分数据点可以补偿双脉冲光谱的分辨率。Anderson等[16]将GA-PLS应用于优化“好奇”号火星探测器上ChemCam仪器对岩石的远程定量分析,该方法能够减少数据量和节省计算时间,对于太空探测和快速分析具有重要意义。

目前,土壤元素的LIBS定量分析方法主要有基本定标法[17]、内定标法[18]、神经网络法[19]和PLS法[20]等。本研究将GA-PLS应用于土壤的LIBS分析,对重金属元素Mn,Cr,Cu,Pb,Ba和氧化物Al2O3,CaO,Fe2O3,MgO,Na2O和K2O进行定量分析。通过与传统PLS方法的结果比较,证实了GA-PLS方法对土壤成分定量分析具有更高的准确度。

2 实验部分

2.1 实验装置

实验装置如图1所示。实验在空气环境下进行。采用调Q开关Nd:YAG脉冲激光器(Beamtech, Nimma 400,波长532 nm,重复频率3 Hz,脉冲宽度8 ns),激光能量为40 mJ/脉冲。激光经过反射镜和平凸透镜(焦距10 cm)聚焦到样品表面,样品放置在二维电动平台上作“弓”字形运动。为了防止击穿空气,焦点位于样品表面下方2 mm处。激发出的等离子体辐射光由光收集器收集并耦合到光纤中(光纤收集信号的角度为15°),传输至光谱仪(Andor Technology,Mechelle 5000,波长范围200～950 nm,分辨率 λ/Δλ=5000)进行分光,光谱仪配备增强型电荷耦合器件(ICCD)(Andor Technology,iStar DH-334T 1024×1024像素)用于光电转换。最后将数据传输至计算机进行分析和处理。

为了获得较高的光谱强度和信背比,ICCD门控采用时间积累模式,采集延迟时间设为4 μs,门宽设为10 μs。为了降低激光脉冲能量波动对光谱强度的影响,每张光谱在样品不同位置积累60个脉冲,每个样品重复采集6次。

图1 LIBS实验装置原理图Fig.1 Schematic diagram of the experimental setup

2.2 样品制备

由于PLS模型应用于大样本数据中能获得更高的准确性,因此需要大量不同浓度的样品用于定量分析。选用4种国家标准土壤样品编号分别为GBW(E)070008,GBW(E)070009,GBW07404和GBW07405,土壤中重金属元素Mn,Cr,Cu,Pb,Ba和氧化物Al2O3,CaO,Fe2O3,MgO,Na2O,K2O, SiO2的含量如表1所示。每2种标准样品按配比分别为1∶9,2∶8,……,9∶1配制9种不同浓度的样品,经称量、搅拌、研磨使样品混合均匀,共配制得到54个样品。采用硼酸镶边垫底法对样品压片,压强20 MPa,保压3 min,制成直径4 cm,厚度3 mm的薄片。对于每种分析元素,各自将58个样品(4个标准样品和54个自制样品)按浓度从低到高编号,从中等间隔取出第1,3,……,57号样品(共29个)作为定标集,第2,6,……,58号样品(共15个)作为监控集,第4,8,……, 56号样品(共14个)作为预测集。由于每个样品重复采集6次,定标集、监控集和预测集分别包含174, 90和84幅光谱。GA-PLS程序在Matlab R2010b环境下编写。

表1 土壤标准样品的主要成分和含量Table 1 Major compositions and concentrations of standard soil samples

3 结果与讨论

3.1 光谱数据的选取

土壤样品的LIBS光谱很复杂。将美国国家标准与技术研究院(National Institute of Standards andTechnology,NIST)的标准原子光谱数据库[21]与实际样品中分析元素的特征谱线逐一比对,得到了土壤中所含分析元素对应的部分特征谱线波长,以及用于分析和优化的光谱区间,如表2所示。这里的特征谱线是指谱线强度较高且能够分辨的谱峰。对于PLS模型,选取包含分析元素多条特征谱线的光谱区间(5～45 nm)内的所有波长离散点强度值作为光谱数据;而对于GA-PLS模型,通过GA从给定的光谱区间内挑选出部分强度值作为光谱数据。为了降低实验参数波动的影响,提高定量分析的精度,在建模之前需要对光谱做归一化处理。选择土壤中的主要元素Si的288.16 nm谱线作为内标线,所有谱线的强度均除以内标线强度。

表2 土壤中所含元素、对应的特征谱线波长和光谱区间Table 2 Compositions of soils,corresponding characteristic wavelengths and spectral regions

3.2 PLS模型

将分析元素对应的光谱区间内的所有强度值作为PLS的自变量,分析元素浓度作为因变量,采用定标集建立定标模型。在PLS建模过程中,主成分个数的确定至关重要,关系到模型的稳定性和准确性。为了考察模型的预测能力,将PLS模型应用于监控集,根据监控集样品预测浓度的残差平方和(PRESS)确定主成分个数。以Mn元素为例,PRESS随主成分个数(取前30个主成分)的变化情况如图2所示。PRESS最小时对应的最佳主成分个数是6,因此取6个主成分对Mn元素的定标集建立PLS模型。

图2 Mn元素的残差平方和(PRESS)随主成分个数的变化趋势Fig.2 Variation tendency of predicted residual error sum of squares(PRESS)with different numbers of principle components(PCs)for Mn

3.3 GA优化谱线选择

GA的主要影响因素有适应度函数(目标函数)、种群数目、终止代数、选择、交叉和变异算子等。遗传算法进行谱线选择的主要步骤为:

(1)编码 将光谱区间中的每一个波长作为染色体的一个基因,采用0-1编码。若编码为“1”,则该波长处的强度值参与PLS建模;若编码为“0”,则该波长处的强度值不参与建模。

(2)种群初始化 设定种群数目为200,采用随机初始化的方式,随机产生200条二进制编码的染色体。

(3)评价 首先对染色体进行解码,将染色体中所有编码为“1”的基因对应的波长处的强度值代入PLS进行建模,PLS中主成分个数由3.2节所述方法确定。然后计算该条染色体的适应度函数,设定适应度函数为监控均方根误差(RMSEM)。RMSEM表示监控集样品浓度预测的均方根误差(RMSE),此函数也是GA待优化的目标函数。RMSEM越小,暗示模型的预测准确性越高。

(4)选择、交叉和变异操作 采用轮盘赌选择和单点交叉方法。交叉概率和变异概率分别设为0.5和0.1。

(5)最优谱线组合 重复步骤 (3)和(4)至最大遗传代数,设定终止代数为300。以目标函数RMSEM最小时的基因编码解码后得到的谱线组合作为最优谱线组合。

以Mn元素为例,每一代中所有种群的RMSEM的最小值随遗传代数的变化情况如图3所示。RMSEM的最小值随遗传代数的增大逐渐收敛,趋近于0。因为GA随机初始化种群,所以每次运行GA-PLS程序产生的结果会略有差异。在进行谱线选择时运行5次GA-PLS程序,产生5组待选谱线组合,同样以RMSEM为评价标准从中选出最优谱线组合。选取GA优化后的谱线用PLS对定标集建模,然后对监控集和测试集样品浓度进行预测。

图3 Mn元素的监控均方根误差随遗传代数的变化趋势Fig.3 Variation tendency of root-mean-square error of monitoring (RMSEM)with different genetic generations for Mn

3.4 定量分析结果对比

以Mn元素为例,用于建立PLS和GA-PLS模型的谱线如图4所示,图中“↓”指向Mn的7条特征谱线。通过GA优化谱线选择后,谱线数目从原来的1042条减少至466条。从图4可见,对于Mn的单峰,优化后的谱线选择依然保留谱峰;而对于Mn的重叠峰,由于多条谱线叠加后的谱峰强度并不能反映原子特征谱线的真实强度,所以GA并没有选择重叠谱峰参与PLS建模,说明GA对于重叠峰干扰有一定的识别能力,可以在一定程度上降低重叠峰对定量分析结果的影响。Mn元素的定量分析结果如图5所示,使用GA-PLS模型后,定标集的RMSEC从0.0158%降低为0.0008%,预测集的预测均方根误差(RMSEP)从0.0215%降低为0.0167%,预测集的平均百分比误差(MPE)从8.10%降低为5.20%。可见,GA-PLS模型的定标和预测准确度明显高于PLS模型。由于只有少于一半的光谱数据应用于PLS模型中,并且GA-PLS模型的定量分析结果更好,说明GA有效地去除了与分析元素Mn浓度无关的噪声信号干扰,从而提高了定量分析的准确度。

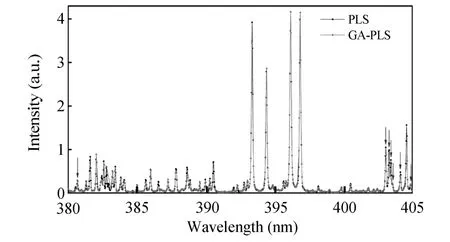
图4 建立Mn元素的PLS和GA-PLS模型的谱线Fig.4 Spectral lines of Mn used for building partial least squares(PLS)and genetic algorithm(GA)-PLS models

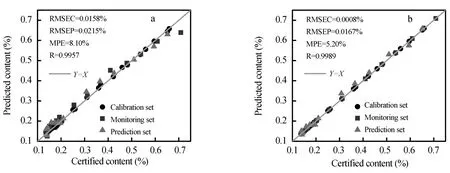
图5 Mn元素的定量分析结果对比Fig.5 Comparison of quantitative analysis results of Mn (a)PLS model;(b)GA-PLS model.

分别应用PLS模型和GA-PLS模型对土壤中的其余10种组成成分Cr,Cu,Pb,Ba,Al2O3,CaO, Fe2O3,MgO,Na2O和K2O的含量进行预测,表3列出了全部定量分析结果,表中阴影表示两种模型中更优的数据。从建模过程中使用的谱线数目可以看出,与传统的PLS模型相比,GA-PLS模型中自变量的数目明显减少,简化了模型。主成分个数与PLS保持相等或略有增加。从表征模型定标准确度的RMSEC来看,除Fe2O3外的所有分析成分的GA-PLS模型的RMSEC值都降低,说明GA-PLS模型的定标效果更好。从表征模型预测能力的RMSEP和MPE来看,在土壤的11种组成成分中有7种成分的GA-PLS模型的RMSEP值更小,有8种成分的GA-PLS模型的MPE值更小。因此,对于多数组分, GA-PLS模型能够显著改善传统PLS模型的预测精度。而对于少数组分,GA-PLS模型比PLS模型的预测精度差,是由于GA在优化谱线选择的过程中去除了光谱区间内的一部分有用信息,因此GA-PLS模型有待进一步改进。

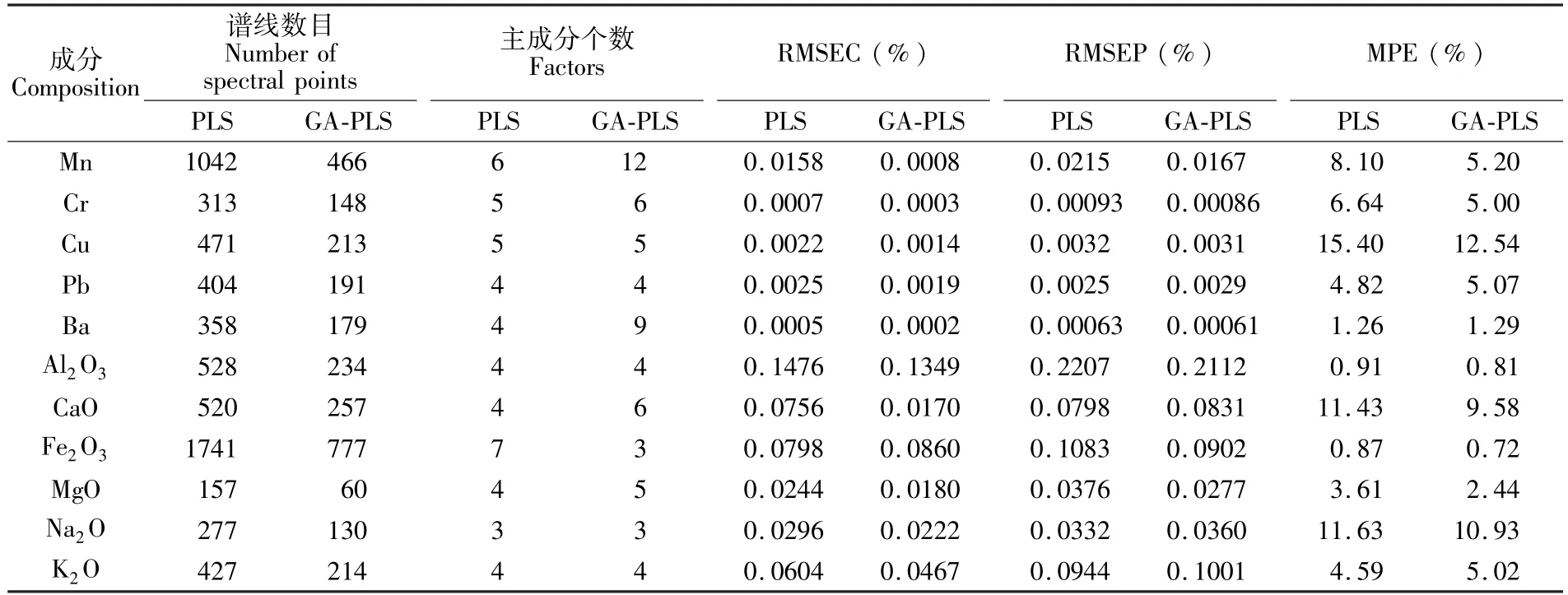
表3 PLS和GA-PLS模型定量分析结果对比Table 3 Comparison of quantitative analysis results between PLS and GA-PLS models

4 结 论

本实验将GA-PLS模型应用于土壤的LIBS定量分析,对Mn,Cr,Pb,Ba,Al2O3,CaO,Fe2O3等11种组分的含量进行预测。结果表明,与传统的PLS方法相比,GA-PLS可以有效去除光谱中重复、多余或不相关的变量,减少用于PLS建模的光谱谱线的数目,从而减少建模的时间,简化模型。对于土壤中的多数组分,GA-PLS模型能够显著改善传统PLS模型的预测能力;而对于少数组分,GA-PLS模型比PLS模型的预测精度差,此部分GA-PLS模型的改进将是下一步研究的重点。

1 Wang Z,Yuan T B,Hou Z Y,Zhou W D,Lu J D,Ding H B,Zeng X Y.Front.Phys.,2014,DOI:10.1007/s11467-013-0410-0

2 Lee W B,Wu J Y,Lee Y I,Sneddon J.Appl.Spectrosc.Rev.,2004,39(1):27-97

3 SHAO Yan,ZHANG Yan-Bo,GAO Xun,DU Chuang,LIN Jing-Quan.Spectroscopy and Spectral Analysis,2013,33(10): 2593-2598

邵妍,张艳波,高勋,杜闯,林景全.光谱学与光谱分析,2013,33(10):2593-2598

4 LU Cui-Ping,LIU Wen-Qing,ZHAO Nan-Jing,LIU Li-Tuo,CHEN Dong,ZHANG Yu-Jun,LIU Jian-Guo.Acta Phys. Sin.,2011,60(4):045206

鲁翠萍,刘文清,赵南京,刘立拓,陈东,张玉钧,刘建国.物理学报,2011,60(4):045206

5 Freedman A,Jr.F J I,Wormhoudt J C.Spectrochim.Acta,B,2005,60:1076-1082

6 Gonzaga F B,Pasquini C.Spectrochim.Acta,B,2008,63:56-63

7 Yuan T B,Wang Z,Liu S L,Fu Y T,Li Z,Liu J M,Ni W D.J.Anal.At.Spectrom.,2013,28:1045-1053

8 Braga J W B,Trevizan L C,Nunes L C,Rufini I A,Jr.D S,Krug F J.Spectrochim.Acta,B,2010,65:66-74

9 XU Lu,SHAO Xue-Guang.Methods of Chemometrics.Beijing:Science Press,2004:218-235

许禄,邵学广.化学计量学方法.北京:科学出版社,2004:218-235

10 Bangalore A S,Shaffer R E,Small G W.Anal.Chem.,1996,68:4200-4212

11 Leardi R.J.Chemometrics,2000,14:643-655

12 Breitkreitz M C,Jr I M R,Rohwedder J J R,Pasquini C,Filho H A D,Jose G E,Araujo M C U.Analyst,2003,128: 1204-1207

13 CHU Xiao-Li,YUAN Hong-Fu,WANG Yan-Bin,LU Wan-Zhen.Chinese J.Anal.Chem.,2001,29(4):437-442

褚小立,袁洪福,王艳斌,陆婉珍.分析化学,2001,29(4):437-442

14 Fink H,Panne U,Niessner R.Anal.Chem.,2002,74(17):4334-4342

15 Gottfried J L,Harmon R S,Jr.F C D L,Miziolek A W.Spectrochim.Acta,B,2009,64:1009-1019

16 Anderson R B,Morris R V,Clegg S M,Bell J F,Wiens R C,Humphries S D,Mertzman S A,Graff T G,Mcinroy G R. Icarus,2011,215:608-627

17 Unnikrishnan V K,Nayak R,Aithal K,Kartha V B,Santhosh C,Suri B M.Anal.Methods,2013,5:1294-1300

18 Ebinger M H,Norfleet M L,Breshears D D,Cremers D A,Ferris M J,Unkefer P J,Lamb M S,Goddard K L,Meyer C W.Soil Sci.Soc.Am.J.,2003,67:1616-1619

19 Haddad J E,Villot-Kadri M,Ismael A,Gallou G,Michel K,Bruyere D,Laperche V,Canioni L,Bousquet B.Spectrochim.Acta,B,2009,79-80:51-57

20 Martin M Z,Mayes M A,Heal K R,Brice D J,Wullschleger S D.Spectrochim.Acta,B,2013,87:100-107

21 Kramida A E,Ralchenko Y,Reader J.http://physics.nist.gov/asd

This work was supported by the National Major Scientific Instrument and Equipment Development Project(No.2011YQ160017),the 54-class General Financial Grant from the China Postdoctoral Science Foundation(No.2013M542014),and the Fundamental Research Funds for the Central Universities of Ministry of Education of China(Nos.CXY13Q021,CXY13Q022)

Quantitative Analysis of Soil by Laser-induced Breakdown Spectroscopy Using Genetic Algorithm-Partial Least Squares

ZOU Xiao-Heng,HAO Zhong-Qi,YI Rong-Xing,GUO Lian-Bo,SHEN Meng, LI Xiang-You*,WANG Ze-Min,ZENG Xiao-Yan,LU Yong-Feng
(Wuhan National Laboratory for Optoelectronics,Laser and Tera-Hertz Technology Division, Huazhong University of Science and Technology,Wuhan 430074,China)

Laser-induced breakdown spectroscopy(LIBS)was used to detect the compositions of soil in the air,and the quantitative analysis model with genetic algorithm-partial least squares(GA-PLS) was established.A total of fifty-eight soil samples were split into calibration,monitoring and prediction sets. Eleven soil compositions including Mn,Cr,Cu,Pb,Ba,Al2O3,CaO,Fe2O3,MgO,Na2O,and K2O were quantitatively analyzed.The results demonstrated that,as a pretreatment method for optimizing the selection of spectral lines,GA could be effectively used to reduce the number of spectral lines for use in building PLS model,and hence simplify the quantitative analysis model.More importantly,for most of the soil compositions, GA-PLS could significantly improve the prediction ability compared with the conventional PLS model.Take Mn as an example,the root-mean-square error of prediction(RMSEP)was decreased from 0.0215% to 0.0167%,and the mean percent prediction error(MPE)was decreased from 8.10%to 5.20%.The research provides an approach for further improving the accuracy of LIBS quantitative analysis in soil.

Laser-induced breakdown spectroscopy; Geneticalgorithm; Partialleastsquares; Soil compositions analysis

6 August 2014;accepted 29 October 2014)

2014-08-06收稿;2014-10-29接受

本文系国家重大科学仪器设备开发专项(No.2011YQ160017),中国博士后科学基金(No.2013M542014)和中央高校基本科研业务费(Nos.CXY13Q021,CXY13Q022)资助

*E-mail:xyli@mail.hust.edu.cn

10.11895/j.issn.0253-3820.140668