改进的MIMO系统盲均衡算法
高亚兰,浮盼盼,崔 琳
宿州学院信息工程学院,安徽宿州,234000
改进的MIMO系统盲均衡算法
高亚兰,浮盼盼,崔 琳
宿州学院信息工程学院,安徽宿州,234000
为了提高收敛速度,降低稳态误差,提高常模算法在MIMO系统中的性能,在算法设计上用对数正态误差函数来克服常数模误差函数不对称所带来的缺陷,用时变步长代替固定步长化解收敛速度与剩余误差之间的矛盾。理论分析和仿真结果表明,提出的MIMO系统的对数正态误差函数变步长盲均衡算法与CMA算法相比,能获得更快的收敛速度及更小的均方误差。
对数正态误差函数;MIMO系统;变步长
多输入多输出(MIMO)无线通信系统,在频率带宽和功率都有严格限制的情况下可获得信道容量的成倍增加,能够满足现代人们对通信系统容量和速率不断提高的需求,因此具有重要的研究价值。在很多通信环境下,存在许多引起估计的信道信息错误的因素,想要得到性能优良的通信系统,在设计时必须要考虑到这些因素。处于复杂的衰落环境中的MIMO系统,必须采用均衡技术消除信道干扰和码间干扰。盲均衡技术不需要发射周期性训练序列,是消除ISI的有效途径。
误差函数直接影响着均衡器的性能,本文利用正态误差函数来消除常数模的误差函数的不对称所带来的缺陷,提高均衡器的均衡效果,提出的多用户对数正态误差函数变步长盲均衡算法通过变步长来加快收敛速度,降低了均方误差。
1 多输入多输出系统模型
图1为m路输入n路输出的MIMO系统模型,第i路接收信号和第j路均衡器输出信号可表示为
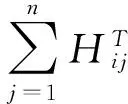
(1)
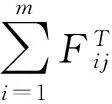
(2)
式中:
Aj(k)=[αj(k)…αj(k-N+1)]T
(3)
Yi(k)=[yi(k)…yi(k-L+1)]T
(4)
yi(k)为第i路的接收信号,aj(k)为第j路的发射信号且相互之间独立,均值为零;wi(k)是叠加在第j路接收信号上的白噪声。对于图1所示的MIMO系统,原有的m路信号之间叠加和相互干扰后,变成了n路信号,必须取n≥m才能在接收端恢复源信号。
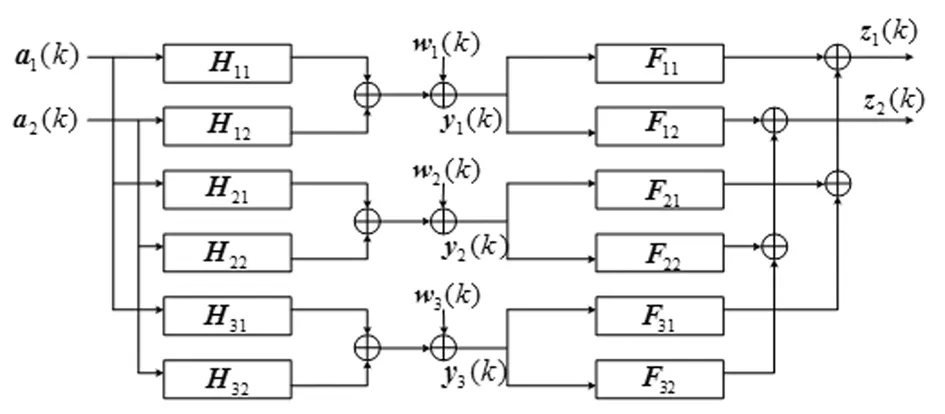
图1 MIMO系统模型
2 对数正态误差函数及特性
传统的多用户常数模算法的代价函数表示为:
(5)
式中e(k)=|zj|2-1
(6)
将对数正态误差函数作为评价均衡器性能的误差函数,以克服常数模误差函数不对称所带来的缺陷,即:
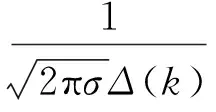
(7)
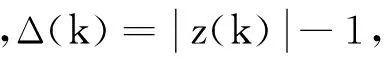
对数正态误差函数e(k)有以下特性。
(1)e(k)具有奇对称性,这是因为
e(-Δ(k))
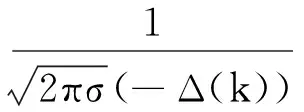
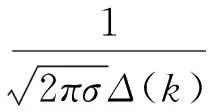
=e(-Δ(k))
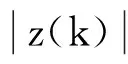
(2)随着σ和μ增大e(k)的值域减小,σ或μ值一定时,e(k)的值随着另一个参数的变小而变大,因此,选择较小的σ和μ,可以获得较快的收敛速度,但这会带来较大的均方误差。
3 多用户对数正态误差函数的变步长盲均衡算法
(8)
式中,E表示统计期望,F是Lm×n的均衡器矩阵。其中:
fij=[Fij(0)…Fij(L-1)]T
(9)
将评价均衡器性能的误差函数定为对数正态误差函数,用随即梯度算法最小化代价函数J1(F)时,F表示为:
F(k+1)=F(k)-λY*(k)Z(k)
(10)
式中:
Y=[Y1T(k)…YmT(k)]T
(11)
Z(k)=[(|z1(k)|2-1)z1(k) … (|zn(k)|2-1)zn(k)]
(12)
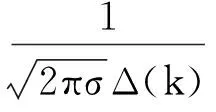
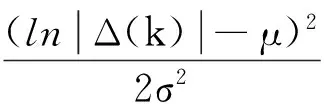
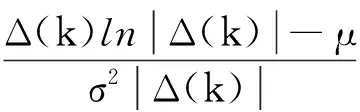
(13)
式中,*表示共轭,γ是固定步长。式(8)称为多用户对数对数正态误差函数的常数模盲均衡算法(LECMA)。
为了加快LECMA的收敛速度,将算法的固定步长γ改为变步长γ(k),即:
(14)
将式(14)代入式(10)就可得到基于对数正太误差函数的变步长盲均衡算法(LVCMA)。
4 仿真实验
仿真信道如下:
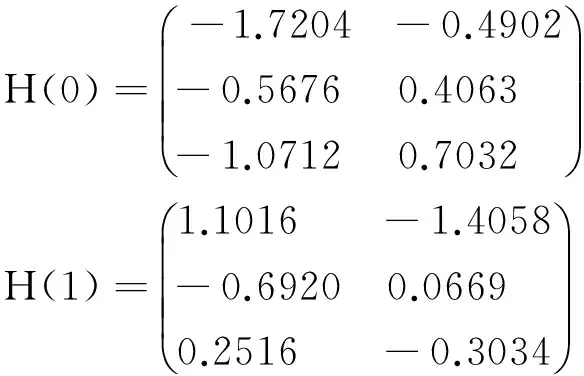
发射信号为两路16QAM,信噪比为20 dB,CMA的第1个均衡器第2个抽头系数为1,第2个均衡器第6个抽头系数为1;LECMA的第1个均衡器第6个抽头系数为1,第2个均衡器第8个抽头系数为1;LVCMA的第1个均衡器第4个抽头系数为1,第2个均衡器第6个抽头系数为1,其余为0。CMA的步长为γCMA=4×10-5,LECMA中的α=7.2×10-8,β=2×10-8,LVCMA中的α=1.9×10-8,β=8×10-8。1000次蒙特卡洛仿真结果,如图2所示。
图2(a)(b)表明LVCMA的误差最小,且3种均衡方法都可以让误差函数收敛到一个较小的误差。CMA的收敛速度比LECMA慢约4 000步,LECMA的误差函数曲线收敛速度比LVCMA慢约7 000步;由图2(c)~(h)可以看出,LVCMA的均衡器输出星座图更加集中清晰,可以得到更好的均衡效果。
5 结束语
针对常数模算法在多输入多输出系统应用中的缺点,本文将传统的常数模盲均衡算法的误差函数改进为对数正态误差函数,并将变步长引入到盲均衡算法中,成功地应用到MIMO系统中。用变步长代替传统CMA中的固定步长可以加快收敛速度,使改进的算法能够获得更快的收敛速度。仿真结果显示,通过对算法的改进,均衡器的性能在很大程度上得到了改善。
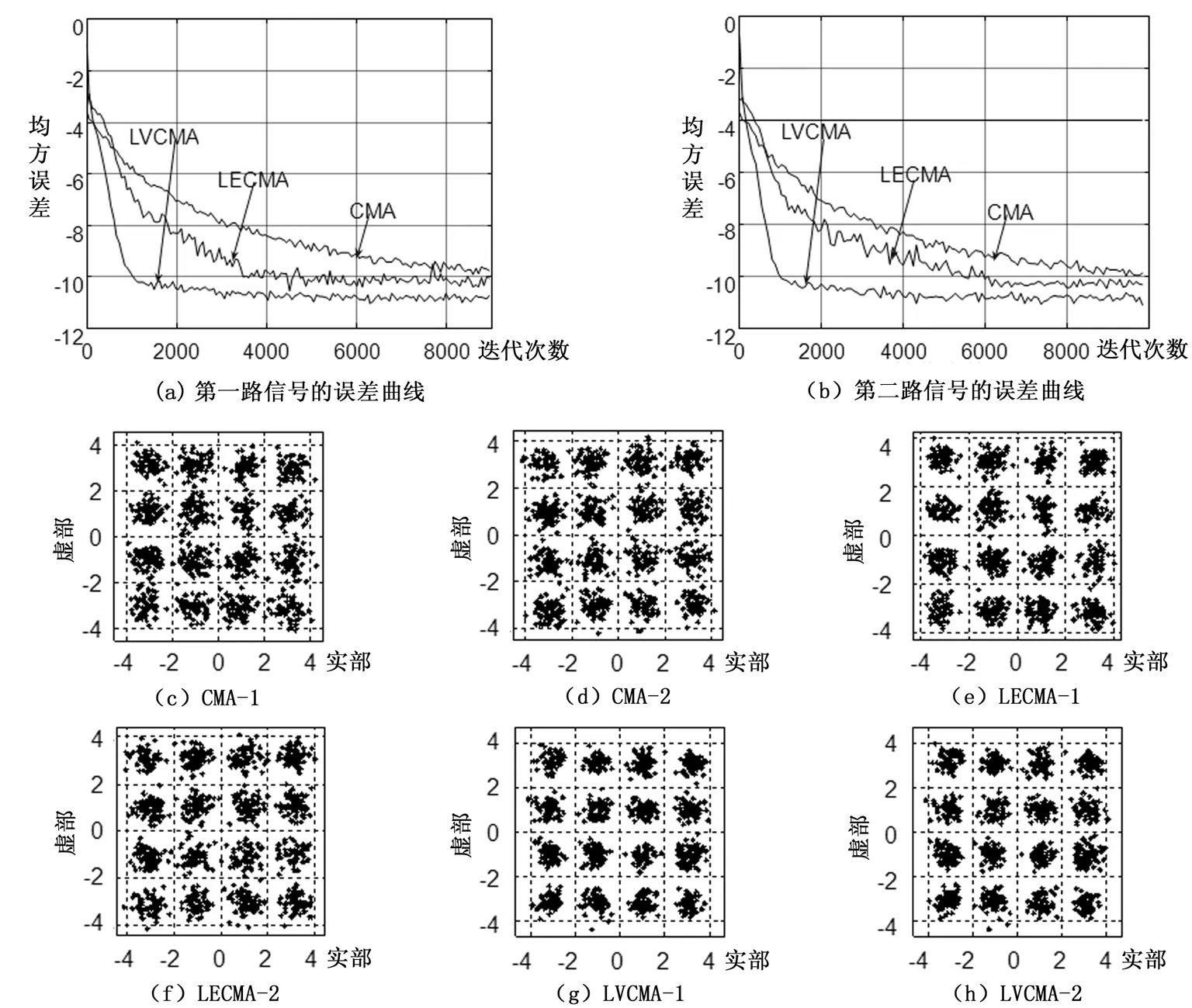
图2 仿真结果
[1]郭业才,何龙庆,韩迎鸽,等.盲均衡技术在水声信道均衡中的应用进展[J].舰船科学技术,2007,29(2):22-27
[2]Doroslovacki M,Fan H.Wavelet-based Linear System Modeling and Adaptive Filtering[J].IEEE Trans on SP,1996,44(5):1156-1167
[3]赵文侃,赵乐军.基于矩阵逆幂法的SIMO信道模型盲均衡方法[J].通信技术,2009,42(5):23-25
[4]易清明.标准SIMO信道盲解卷固定点算法[J].东南大学学报:自然科学版,2008,38(4):574-578
[5]许华,郑辉.一种对Bussgang类盲均衡算法的简单初始化方法[J].系统仿真学报,2005(17):217-279
[6]马康红.水声数字通信系统研究[D].西安:西北工业大学电子信息学院,2001:46-50
[7]焦李成,郑建忠.多径CDMA信道下最小均方盲空时多用户检测[J].电子学报,2002,30(7):981-985
[8]郭业才.自适应盲均衡技术[M].合肥:合肥工业大学出版社,2007:57-59
[9]郭艳,方大纲,梁昌洪.一种有效的正交化恒模算法[J].北京邮电大学学报,2002,25(1):30-33
(责任编辑:汪材印)
An Improved Blind Equalization Algorithm of MIMO System
GAO Yalan,FU Panpan,CUI Lin
College of Information Engineering,Suzhou University,Suzhou Anhui,China,234000
The purpose of MIMO system blind equalization is to signal demodulation at the same time to improve the spectrum utilization. The norm of the traditional algorithm using fixed step length lead to slow convergence speed and big steady-state error.In order to improve the performance of norm algorithm in MIMO system, the algorithm design uses lognormal error function to overcome the defect caused by the asymmetry of error function and uses the time-varying step size instead of a fixed step to resolve the contradiction between the convergence speed and residual error. Theoretical analysis and simulation results show that compared with the CMA blind equalization algorithm, the algorithm can achieve faster convergence speed and smaller mean square error.
lognormal error function; MIMO system; variable step size
10.3969/j.issn.1673-2006.2015.08.027
2015-05-10
高亚兰(1989-),女,安徽淮南人,硕士,助教,主要研究方向:智能信息处理。
TP212.9
A
1673-2006(2015)08-0091-03

