基于数学形态学的焊缝图像多尺度滤波算法研究

王慧玲，尤菲菲，李 絮

1.阜阳师范学院计算机与信息工程学院，安徽阜阳，236032；2.绥化学院信息工程学院，黑龙江绥化，152000

基于数学形态学的焊缝图像多尺度滤波算法研究

王慧玲1，尤菲菲2，李 絮1

1.阜阳师范学院计算机与信息工程学院，安徽阜阳，236032；2.绥化学院信息工程学院，黑龙江绥化，152000

采用含有圆孔型缺陷的焊缝图像作为研究对象，针对这类焊缝图像的特点，对焊缝图像进行灰度级变化，增加图像的动态范围；同时将数学形态学滤波算法与焊缝图像相结合，利用多尺度形态学滤波算法对含燥图像进行处理，达到同时去除高斯噪声与椒盐噪声的目的。实验结果表明，该算法较传统方法具有较好的处理效果。

焊缝图像；高斯噪声；椒盐噪声；滤波

随着焊接技术的不断发展，焊缝位置的自动化实时检测已成为焊缝图像处理过程中的重要研究课题，寻找一种快速、准确的焊缝图像处理方法，是整个焊缝缺陷检测的重要内容[1-2]。

本文针对焊缝图像的特点，利用多尺度形态滤波算法对含有噪声的焊缝图像进行降噪处理，并与传统降噪算法进行对比，实验结果表明，该算法具有更好的处理效果。

1 数学形态学理论

数学形态学摒弃了传统的分析方法，它是以集合论为基础，着重研究图像几何结构的理论。它的基本思想是通过构造结构元素去探测图像的特定形状，达到识别图像的目的。

1.1 灰度形态学基本运算

数学形态学最基础的运算是膨胀与腐蚀运算，以及在此基础上复合而成的开、闭等运算。

利用结构元素b对灰度图像f的腐蚀定义为：

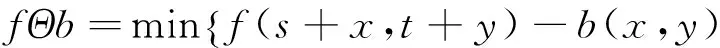
(1)

结构元素b对灰度图像f的膨胀定义为：

(2)

开运算的定义：

（1）《健康评估实训报告册》的使用缩短了学生书写实训报告的时间，将学生从繁重的实训报告书写中解放出来。

fΟb=(fΘb)⊕b

(3)

闭运算的定义：

f·b=(f⊕b)Θb

(4)

在灰度形态学的四种基本运算中，腐蚀运算会收缩图像较亮区域的边缘，消除物体的边界点，去除小于结构元素的物体。膨胀运算则恰恰相反，它具有填补空洞功能，同时使物体的边界向外扩张。开、闭运算都具有平滑图像边缘的功能，其中开运算具有消除毛刺和孤立的小点以及小的亮区域的功能，闭运算在消除凹沟的同时可以填补图像中细小空穴和尺寸较小的暗区域。

2 焊缝图像处理过程

焊缝图像在采集、传输过程中，往往包含了很多噪声和飞溅、烟尘、弧光等干扰，使得图像的质量下降，因此，必须使用适当的方法对焊缝图像进行降噪处理，以保证缺陷检测的后续处理能顺利进行。

2.1 焊缝图像去噪

本文处理的图像是圆环型的焊缝图像，它是一个对称图形，根据图像本身可能存在的气孔、点状夹杂的缺陷，在滤波的同时需要保留这些重要的细节性信息。形态学的开、闭运算具有在不改变图像面积的情况下，可以断开狭窄的间断、消除细小的突出物，同时使对象的轮廓变得平滑。本文算法如下：

(1)对图像进行灰度级变换，增强图像的动态范围。从图2可以看出，采集的焊缝图像的局部气孔缺陷部位与背景对比度不高，同时图像边缘模糊，对图像进行灰度级变换可以增强图像对比度，突出了图像的边缘与缺陷的特征。

(2)选择合适的放大系数对图像进行高频系数与低频系数的适当放大。

(3)选择多结构的结构算子对图像进行形态学开运算处理。结构算子的好坏与否直接影响形态学运算处理的效果，而且不同尺寸，不同结构的算子对图像的处理效果也不相同。根据焊缝图像本身及焊缝缺陷的大小，选择了多个有界且比原图结构简单的凸性算子。本文选择的算子如下所示：

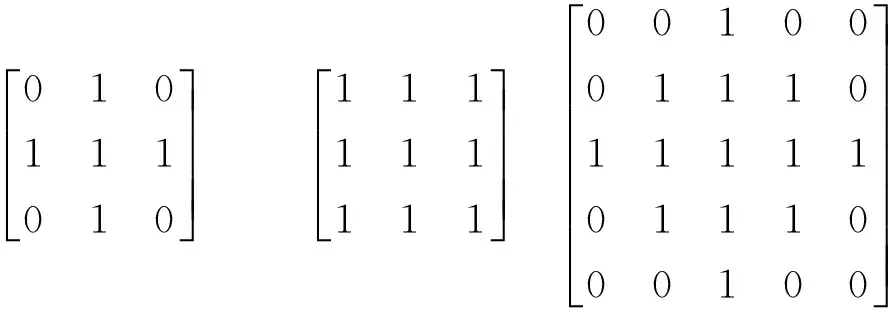
(a)size=1的钻石形 (b)3*3方阵 (c)r=2的圆形

图1 结构算子

(4)使用3*3全方位结构算子对焊缝图像进行形态学闭运算。该过程可以有效地去除小面积的噪声，平滑图像的边缘。

2.2 实验结果及分析2.2.1 图像增强处理

原始焊缝图像是灰度图像，存在前景与背景对比度不强的特点，所以在对图像进行预处理之前，对其进行灰度级变换，即将其灰度从[24,183]映射到[0,255]，处理结果如图2、图3所示。

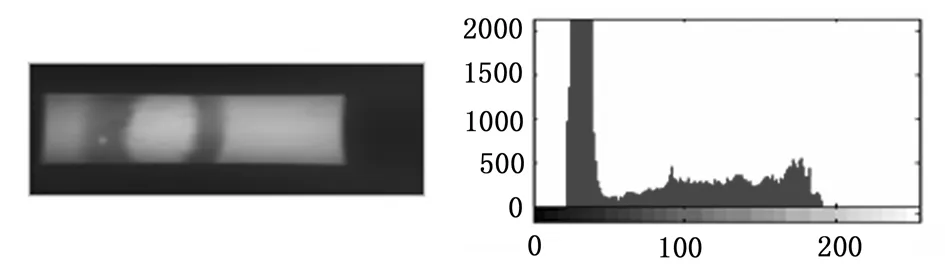
图2 原始焊缝图像及其直方图

2.2.2 多尺度焊缝图像的形态学滤波处理

为了更好地研究算法的滤波效果，对焊缝图像加入方差为0.000 5以及0.02的高斯噪声和0.01的椒盐噪声，处理结果如图4、图5所示。

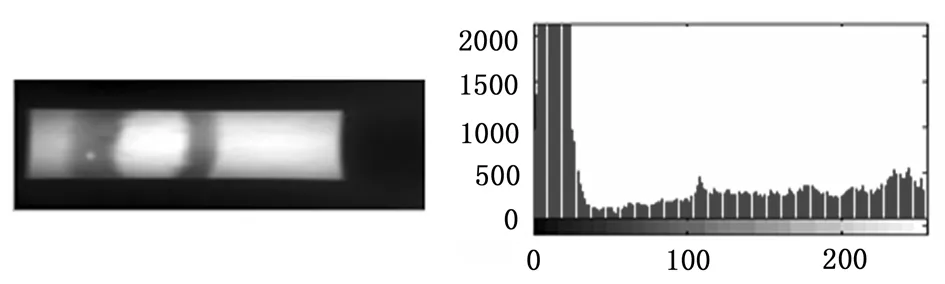
图3 经灰度变换后的图像及其直方图

图4 噪声图像滤波处理比较(方差=0.0005)

由图4可见，当噪声方差较小时，均值滤波的处理效果不够理想，但本文算法与中值滤波的算法处理效果相当。

图5 噪声图像滤波处理结果(方差=0.02)

由图5可见，当噪声方差很大时，中值滤波与均值滤波的效果非常不理想，本文算法对于噪声密度大的图像处理效果较理想。

同时，为了对算法进行定性分析，本文使用NMSE(归一化方差)作为客观评价标准，其取值越小，处理效果越好，如表1所示。

表1 三种去噪算法的NMSE值

3 结束语

本文将数学形态学运算与焊缝图像的去噪算法相结合，针对焊缝图像及气孔类缺陷的特点，选择多尺度的结构算子，同时对焊缝图像实施开、闭运算，以达到降噪效果。实验证明：本文算法对于去除同时含有大密度的椒盐噪声和高方差的高斯噪声效果较理想，可以在滤波的同时达到增强图像边缘的目的，处理效果较好。

[1]岳安志,杨建宇，张超.基于多尺度形态学滤波的高分辨率遥感影像分割[J].农业工程学报，2013,29:89-95

[2]刘燕,王刚,王国栋,等.用于机器视觉的焊缝图像获取及图像处理[J].计算机工程与应用,2014,50(3):135-141

[3]王月红.图像分割算法综述与探索[J].科学时代,2010(4):132-134

[4]王勇,郭慧.基于形态学的焊缝X射线图像缺陷检测[J].东华大学学报：自然科学版，2013,39(4):460-463

[5]薛丽霞，李涛，王佐成.自适应的形态学边缘检测算法[J].计算机工程，2010,36(23):214-216

[6]MOGHADDAM A A,RANGARAJAN L. A method for detection welding defects in radiographic images[J].International Journal of Machine Intelligence,2011(4):307-309

[7]ALAKNANDA,ANAND R S,KUMAR P.Flaw detection in radiographic weldment images using morphological watershed segmentation technique[J].NDT&E International,2009,42(1):2-8

[8]刘国宏,郭文明.改进的中值滤波去噪算法应用分析[J].计算机工程与应用，2010，46(10)：187-189

[9]邹怡蓉,都东,曾锦乐，等.基于多视觉特征获取与信息融合的焊道识别方法[J].焊接学报，2013(5):33-38

[10]王小鹏,郑玉莆.一种图像噪声的形态学多尺度去除方法[J].计算机工程，2006,32(4)：208-210

(责任编辑：汪材印)

10.3969/j.issn.1673-2006.2015.08.026

2015-03-05

阜阳师范学院自然科学研究一般项目“基于数字形态学的焊缝图像缺陷检测技术的研究”(2014FSKJ10)，“改进的蚁群算法在TSP中的应用研究”(2014FSKJ09)。

王慧玲(1982-)，女，安徽宁国人，硕士，讲师，主要研究方向：图像处理。

TP274.4

A

1673-2006(2015)08-0089-03