基于IRML的油气加工系统多层次故障传播模型研究
马 曦,张来斌,胡瑾秋,蔡战胜,2
(1.中国石油大学 机械与储运工程学院, 北京 102249;2.中海石油 中捷石化有限公司, 河北 沧州 061101)
基于IRML的油气加工系统多层次故障传播模型研究
马 曦1,张来斌1,胡瑾秋1,蔡战胜1,2
(1.中国石油大学 机械与储运工程学院, 北京 102249;2.中海石油 中捷石化有限公司, 河北 沧州 061101)
大多数油气加工生产事故是由于系统中相互关联的设备或子系统发生连锁失效而导致,设备或子系统的相互作用关系使故障传播行为呈现复杂性且强非线性的特征,故此,采用基于系统弹性分析建模语言(IRML)的多层次故障传播模型对石油加工复杂系统故障行为特征进行定性、定量分析。该模型分为静态分析模块和动态分析模块,前者静态分析故障传播结构特征,后者通过故障情景模拟动态分析故障演化机理。通过案例分析,建立了常减压蒸馏系统的多层次故障传播模型,分析该系统故障传播行为的静态特征和动态特征。结果表明,多层次故障传播模型适用于油气加工系统复杂且强非线性的故障行为建模,建模参数可表示复杂系统的结构特征和故障传播行为模式,可进一步用于油气加工系统中故障传播趋势预测、故障溯源和柔性诊断等方面的研究。
油气加工系统;多层次故障传播模型;静态分析模块;动态分析模块;故障传播行为;故障演化
油气加工系统本质上是具有结构与功能统一的、开放的复杂动态大系统,它由不同属性的子系统相互关联、相互作用、相互渗透而构成。其安全问题有三大特征,即:(1)物料大多具有易燃易爆性、反应活性、毒性和腐蚀性;(2)生产装置规模大、集成度高,且加工过程具有强非线性;(3)系统组成关系与行为复杂,与环境之间的关联程度高、耦合性强,导致系统故障的形成、传播、演化等具有多样性、随机性、涌现性等特点[1-2]。油气加工系统中任何子系统或其中部件一旦发生故障,常引发连锁反应,造成重大生产损失,甚至导致灾难性的安全事故[3]。在石油加工系统故障行为建模的基础上,研究故障征兆、故障模式、故障传播路径等特征,有助于提高预警系统的报警准确性,并快速准确地提出整改措施和故障后果警示,保证系统的安全,提高系统的弹性。国内外故障行为研究中使用较多的故障传播模型建模方法是符号定向图法(SDG)[4]。SDG法常与危险与可操作分析法(HAZOP)结合,用于复杂系统故障诊断中[5]。然而,SDG模型侧重于理想工况下故障传播途径的描述,而不能表达故障征兆、故障模式等故障行为特征,若研究工况发生变化,有可能引起分析结果与实际情况偏离。
Johansson等[6]提出一种在系统相关性结构模型的基础上分析节点脆性和系统风险的方法。该方法要求掌握详尽的系统工作机理,以得到较准确的响应结果。然而,油气加工系统组成复杂,并且生产工况多变,很难实现全局模拟;而且该方法主要关注于风险后果的分析,忽略了故障传播的过程分析。
多线性事件序列模型[7],如时间和事件序列图(STEP),将事故描述成多个事件序列,系统分解成有因果关系或并行的事件集合。该类方法一定程度上可表示事故的发展,但其主要依靠经验者的主观判断,仅限于静态的定性分析。
功能共振事故模型(FRAM)[7-8]是从系统功能的角度对事故的发展建模,它强调系统内部的功能关系。但该方法功能单元复杂,输出事件发展序列,建模结果单一,目前仅用于静态的定性分析。
除了基于图论方法的故障建模,人工智能方法,如神经网络、专家系统等也成为建立故障传播模型,对复杂系统进行故障诊断的主要方法[9-10]。人工智能方法注重于故障模式的识别,无法分析故障的传播途径及特征,因此在故障溯源方面有一定缺陷,无法有效地辅助安全预警工作。
为了定性定量分析油气加工系统在动态工况下的故障传播特征,笔者在系统弹性分析建模语言(IRML)[11]的基础上提出多层次故障传播模型(HFPM),并以常减压蒸馏系统为例进行案例分析,以实现多层次故障传播建模。
1 用于油气加工系统的多层次故障传播模型
多层次故障传播模型(HFPM)是基于IRML语言提出的适用于油气加工系统故障传播行为建模的方法。分析系统结构特征,并通过模拟故障情景分析油气加工系统的故障传播行为。该模型由静态分析模块和动态分析模块构成。
1.1 静态分析模块
静态分析即结构分析,是根据分析系统的结构组成,得到各节点在特定系统结构下的故障传播特点。
复杂系统的故障传播是节点间相互作用关系的结果。根据这种关系将节点分为危险性节点、脆性节点和相关性节点[2,12]。
危险性集合C(k):节点k相对于直接或间接地依赖于它的节点而言危险性。该集合大小定性地代表节点k的危险性程度。
脆性集合V(k):节点k相对于它依赖的节点而言脆性。该集合大小定性地代表节点k的脆性程度。
相关性集合I(k)=C(k)∩V(k):如果节点k与其他节点(如节点h)相互显现危险性和脆性,则定义为两节点相关。该集合大小定性地代表节点k与其它节点的相关性程度。
多层次故障传播模型静态分析模块分为绘制系统结构图、简化结构图和结构复杂化3个步骤。
(1)绘制系统结构图。故障的传播是通过设备或子系统间物质信息交换实现,故障的传播路径与工艺流程相关,故石油加工生产流程图可在一定程度上反应故障行为特征。在工艺流程图的基础上,根据工艺单元划分出子系统节点,子系统内的设备为次节点,设备间或子系统间的物质和信息的流动路线简化为支路,绘制系统结构图。
(2)简化结构图。油气加工系统结构抽象化,将子系统作为分析节点,得到每个节点的危险性集合、脆性集合和相关性集合,判断子系统节点的危险性和脆性强弱。
(3)结构复杂化。以危险性和脆性较大的子系统作为分析对象,将子系统内的设备作为分析节点,与步骤(2)类似判断其危险性和脆性强弱。
静态分析模块得到最危险子系统与脆性最大子系统,在此基础上进一步得到2个子系统中最危险设备和脆性最大的设备。
1.2 动态分析模块
动态分析模块将故障在系统内的传播行为特征定量化,在不同故障模式和不同工况下分析故障演化趋势。动态分析模块包括故障传播情景分析、确定建模参数、定义状态函数和绘制系统状态函数图4个步骤。
(1)故障传播情景分析。多层次故障传播模型与“如果…怎么样…”法结合,对故障在系统内的传播趋势进行分析,得到每个子系统或设备的事件时间序列[7]。
(2)建模参数。表征故障情景的建模参数有扰动施加时间TD、节点恢复时间TR、节点缓冲时间TF。扰动施加时间是指从扰动施加于初始节点到扰动从初始节点撤离的时间间隔。节点缓冲时间是指节点受到扰动直接作用到节点失效的时间间隔,在实际工况中是指设备某参数受到扰动直到超出正常工况阈值的时间。节点恢复时间是指节点开始恢复到节点恢复的时间间隔,在实际工况中是指设备某参数受控制系统调控从超出正常工况阈值到恢复正常值的时间。多层次故障传播模型应用于实际生产中时,建模参数由当前的生产工况和故障模式决定,通过实验或历史监控数据得到不同生产工况和故障模式下的各参数值。本研究中将参数设置为无量纲,仅作理论研究。
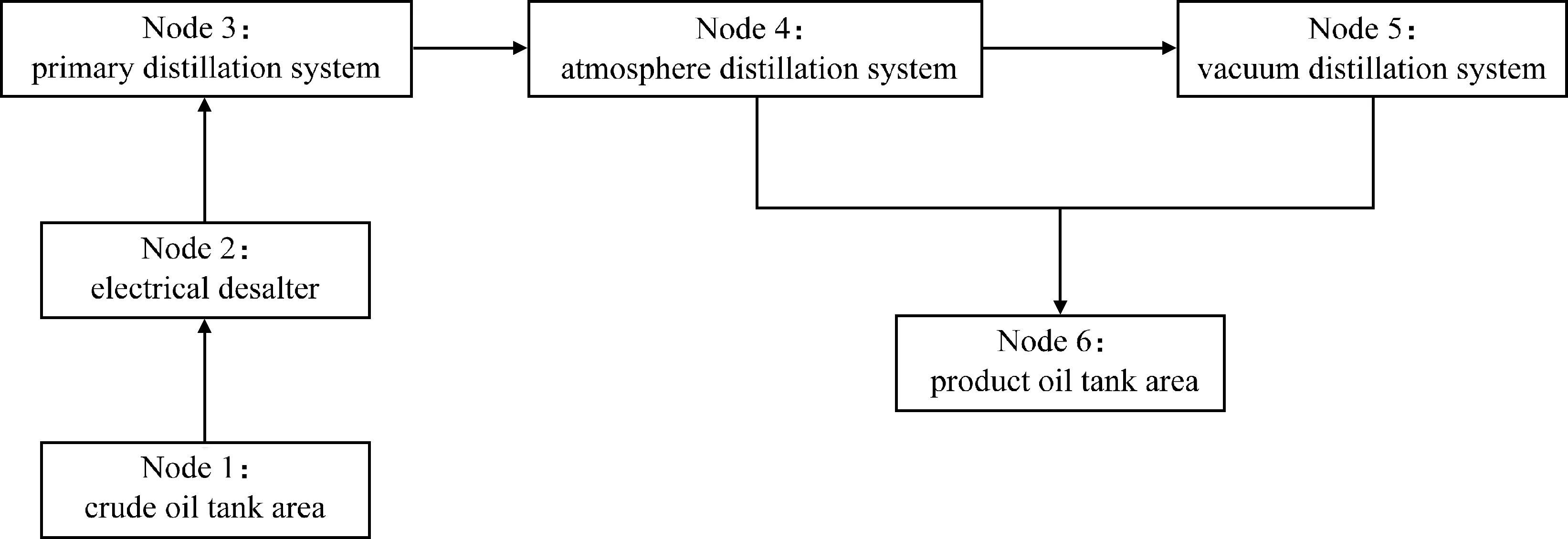
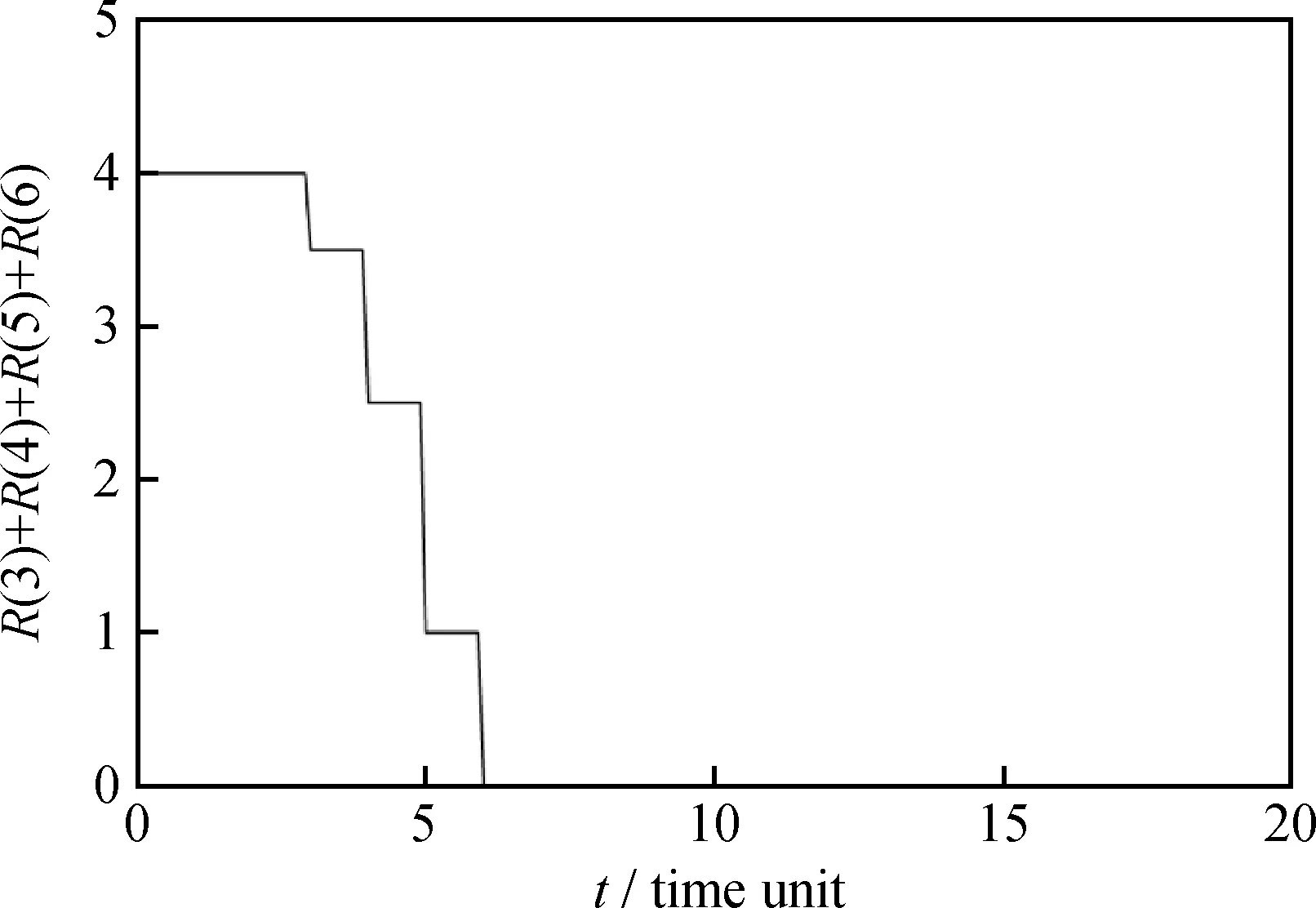
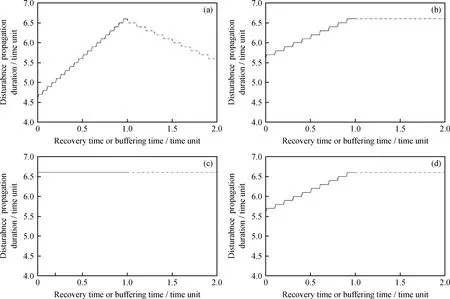
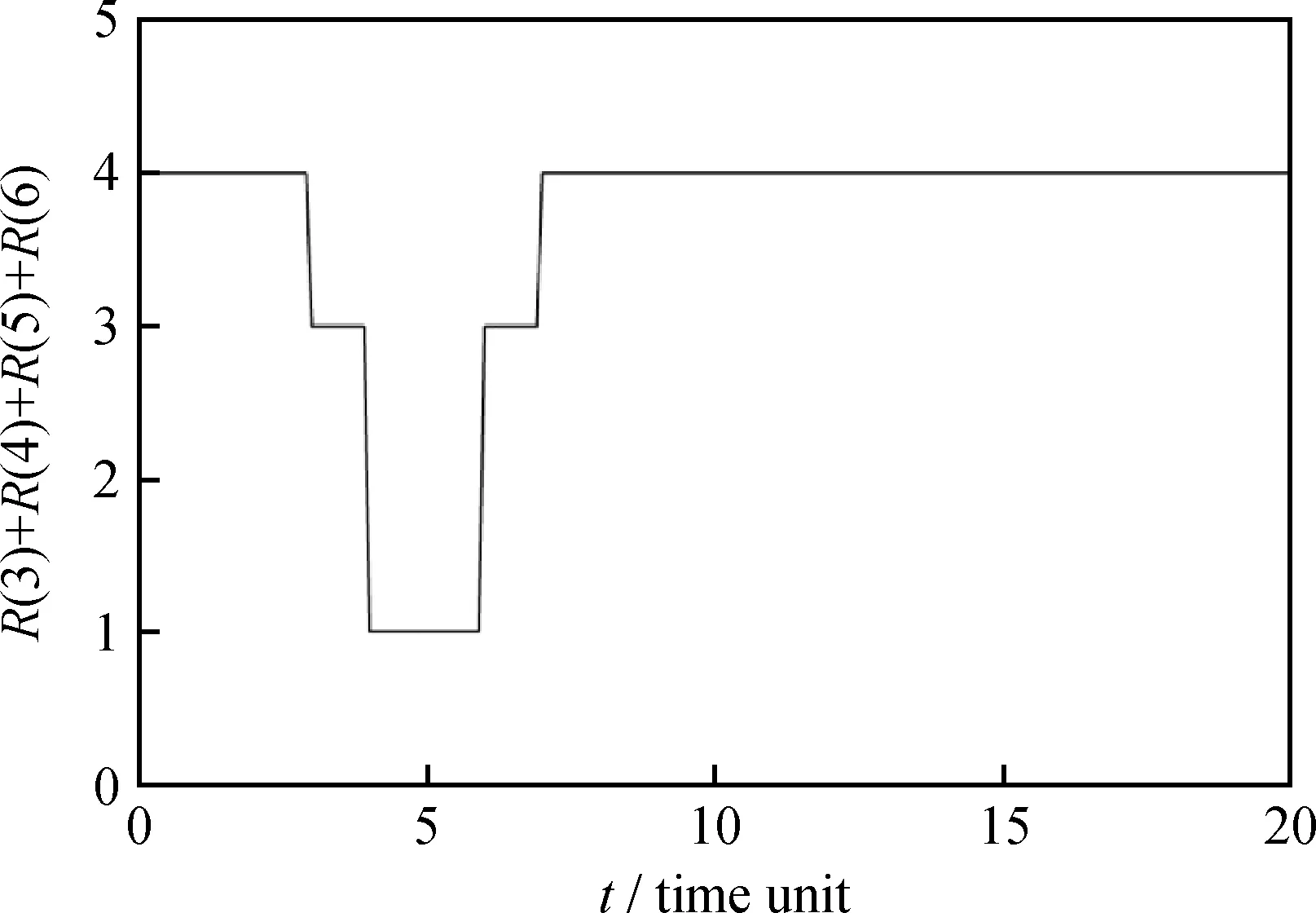
(3)定义状态函数。当次节点处于正常状态时,状态函数r=1;反之,处于故障状态时,状态函数r=0。若某子系统节点i包含n个次节点,则该子系统节点状态函数定义为R(i)=(r(1)+r(2)+r(3)…+r(n))/n,它表示故障在子系统内的传播状态。子系统节点状态函数R=1表示故障未传播至子系统,或子系统已恢复正常状态;R=0表示子系统完全故障,子系统内全部部件处于故障状态;0 整个系统的状态函数可表示为受故障影响的子系统节点的状态函数叠加,在故障传播情景分析和建模参数的基础上建立;函数值大小反映了故障在系统内的传播深度,值越小,故障传播深度越大,系统的故障程度越大。 在常减压蒸馏系统(见图1)中,以初馏塔节点3.1故障为例进行情景分析。节点3.1经过缓冲时间失效后,分别传播至节点3.2和节点4.1,此时故障分两条路径向下层节点传播,直到传播至终节点。在此基础上,由建模参数决定节点状态的事件时间序列,从而得到受故障传播影响的每个子系统节点的状态函数时间序列,如表1~表4。将4个状态函数叠加,得到系统的状态函数。 图1 常减压蒸馏系统结构图 表1 常减压蒸馏系统节点3的状态函数时间序列 Table 1 The sequentially timed state function of node 3 in atmospheric and vacuum distillation system Node3Pre⁃disturbanceDisturbance3 1fails3 2fails3 1recovers3 2recoversTimepointt…t0t0+TF3 1t0+TF3 1+TF3 2t0+TD+TR3 1t0+TD+TR3 1+TR3 2R(3)=[r(3 1)+r(3 2)]/2110 500 51 表2 常减压蒸馏系统节点4的状态函数时间序列 表3 常减压蒸馏系统节点5的状态函数时间序列 表4 常减压蒸馏系统节点6的状态函数时间序列 (4)绘制系统状态函数图。根据步骤(3)得到的节点状态函数时间序列绘制出系统状态函数图像,分析图像得到故障在系统中的传播行为特征。 油气加工系统是自动智能化的复杂巨系统,石油加工过程的生产工艺参数由控制系统,如DCS系统控制。当工艺参数由于故障引起波动而超出控制阈值时,工艺参数会在某一时段出现超出正常阈值的波动,控制系统会通过控制器及时调节参数至正常值,因此检测到的参数值在某一时间段呈现跃变波动的特点,最终恢复至正常值。因此,多层次故障传播模型中定义的双值状态函数R可表示石油加工系统中设备参数的变化特征。故障在检测参数上表现为扰动,案例分析中用“扰动”代替“故障”进行说明。 常减压蒸馏装置是常压蒸馏和减压蒸馏两个装置的总称,是炼油厂加工原油的第1个工序,若其发生故障可能会导致相连加工系统的非正常运转,最终引发事故。 常减压蒸馏系统主要包括6大子系统,即原油罐区子系统、原油脱盐脱水子系统(电脱盐罐)、初馏子系统(初馏塔和常压塔)、常压蒸馏子系统(常压塔和常压汽提塔)、减压蒸馏子系统(减压炉和减压塔)、产品储油罐或管线子系统。子系统之间和子系统内设备之间每时每刻都在进行物质和信息交换,设备间的物质信息流实现故障在子系统内部的传播,而子系统间的物质信息交换通道实现子系统间的故障传播。 根据静态分析模块步骤(1),构造多层次故障传播模型的结构图,如图1所示。 2.1 多层次故障传播模型静态分析 按照1.1节中步骤(2)对图1的常减压蒸馏系统的结构图进行简化,得到如图2所示的简化结构图。静态分析得到相对于每个子系统节点的危险性集合、脆性集合和相关性集合,结果列于表5。由表5可看出,节点1受到扰动,故障传播最广,危险性最大;节点6最易受到扰动的影响,脆性最大。节点1 表示原油罐区,节点6表示产品油罐区,2个子系统节点均仅含1个设备节点,故不需要进行步骤(3) 的分析。得出结论,原油罐区和产品油罐区分别是危险性最大的节点和脆性最大的节点。 图2 常减压蒸馏系统简化结构图 表5 常减压蒸馏系统危险性、脆性、相关性集合 Table 5 The criticality/vulnerability/interdependency set for atmospheric and vacuum distillation system CriticalitysetVulnerabilitysetInterdependencysetNode1C(1)={2,3,4,5,6}V(1)={}I(1)={}Node2C(2)={3,4,5,6}V(2)={1}I(2)={}Node3C(3)={4,5,6}V(3)={1,2}I(3)={}Node4C(4)={5,6}V(4)={1,2,3}I(4)={}Node5C(5)={6}V(5)={1,2,3,4}I(5)={}Node6C(6)={}V(6)={1,2,3,4,5}I(6)={} 2.2 多层次故障传播模型(HFPM)动态分析 2.2.1 扰动模式分类 石油加工系统的故障传播媒介是设备和物料介质,因此扰动模式分为设备扰动模式和介质扰动模式。前者分为单设备和多设备扰动模式,后者分为单处介质和多处介质扰动模式。实例分析中以单设备扰动和单介质扰动为例建立多层次故障传播模型。 2.2.2 设备扰动 以单设备——初馏塔扰动为例(如图3双实线箭头所示),研究单设备扰动下常减压系统中的故障演化行为,即系统抵抗扰动的柔性分析。对于受到多设备扰动的系统,其状态函数值是多个设备扰动下的叠加。若n个设备受到扰动,n个扰动传播至i设备的时间点不同,扰动到达i设备的时间点取n个时间点中的最小值,恢复时间取n个恢复时间的最大值。 扰动波及节点有3、4、5、6节点,在不同工况和扰动条件下,即不同的建模参数条件下,由1.2节中所述步骤(1)~(4)得到系统的状态函数图像,对图像进行特征分析得到系统内故障传播的行为特征。 图3 单设备或单处介质扰动下的HFPM (1)故障情景1:TD=2.5;各次节点缓冲时间和恢复时间参数均设为1。 扰动在2个时间单位时施加于初馏塔(节点3.1),扰动作用2.5个时间单位,绘制出系统的状态函数图像,如图4所示。由图4可以看出,大系统经过一段时间的波动后恢复正常状态。 图4 故障情景1单设备扰动状态函数图像 (2)故障情景2:TD=3.5,缓冲时间和恢复时间同故障情景1。 扰动在2个时间单位时施加于初馏塔(节点3.1),扰动作用3.5个时间单位,绘制出系统的状态函数图像,如图5所示。由图5可以看出,系统经过一段时间的波动后整体发生故障。对比故障情景1、2可以看出,系统在某节点受到扰动的情况下经过一段时间的状态波动后,可能恢复正常状态,也可能发生全局故障。系统抵抗扰动的持续时间与生产工况有关,生产工况决定节点的缓冲时间参数和恢复时间参数,在故障情景2的基础上改变节点时间参数得到故障情景3、4。 图5 故障情景2单设备扰动状态函数图像 (3)故障情景3:TD=3.5;增大缓冲时间,恢复时间不变,各次节点缓冲时间设为1.5,恢复时间设为1。故障情景4:TD=3.5;缓冲时间不变,减小恢复时间,各次节点缓冲时间设为1,恢复时间设为0.5。该两情景的系统的状态函数图像示于图6。 如图6所示,在单设备(初馏塔)扰动下,适当增大缓冲时间或减少恢复时间可改变系统对扰动的响应,促进系统从故障状态恢复至正常状态;在此设定的参数下,两者相比,减少恢复时间比增大缓冲时间能更加快速有效地促进系统的恢复。 设定TD=2.5,绘制得到各节点缓冲或恢复时间参数-扰动持续时间的函数关系图如图7所示。可以看出,不同节点对系统故障传播的敏感性不同,改变某些节点的时间参数不会影响系统扰动传播的时间,如改变节点4、5、6的缓冲时间和节点5的恢复时间,系统的扰动传播时间不变;而减少节点3、4、6的恢复时间,增大节点3的缓冲时间,系统的扰动传播时间缩短,系统恢复加快。 图6 故障情景3/4单设备扰动状态函数图像 图7 单设备扰动系统节点恢复时间或缓冲时间-扰动传播时间函数图像 2.2.3 介质扰动 以单处介质——初馏塔与常压塔间的介质扰动为例(如图3虚线箭头所示),建立多层次故障传播模型。扰动施加于介质时,相邻的上、下游设备同时受到干扰,类似于多设备扰动的故障情景。多介质扰动的情况同理于多设备扰动。 (1)故障情景1:TD=2;各次节点缓冲时间和恢复时间均设为1。 扰动在2个时间单位时施加于初馏塔(节点3.1)至常压塔(节点4.1)的介质中,扰动作用2个时间单位,绘制出系统的状态函数图像,如图8所示。由图8可以看出,大系统经过一段时间的波动后恢复正常状态。 图8 故障情景1介质扰动系统状态函数图像 (2)故障情景2:TD=2.5,缓冲时间和恢复时间同故障情景1。 扰动在2个时间单位时施加于初馏塔(节点3.1)至常压塔(节点4.1)的介质中,扰动作用2.5个时间单位,绘制得到系统的状态函数图像如图9所示。由图9可以看出,系统经过一段时间的波动后整体发生故障。对比故障情景1、2可以看出,大系统某节点受到扰动经过一段时间的状态波动后,可能恢复正常状态,也可能发生全局故障。系统抵抗扰动的持续时间与生产工况有关,生产工况决定节点的缓冲时间参数和恢复时间参数,在故障情景2的基础上改变节点时间参数得到故障情景3、4。 (3)故障情景3:TD=2.5;增大缓冲时间,恢复时间不变,各次节点缓冲时间设为1.5,恢复时间设为1。故障情景4:TD=2.5;缓冲时间不变,减小恢复时间,各次节点缓冲时间设为1,恢复时间设为0.5。绘制得到两情景系统的状态函数图像如图10所示。 由图10可见,在单介质(初馏塔至常压塔介质)扰动下,适当增大缓冲时间或减少恢复时间可改变系统对扰动的响应,促进系统从故障状态恢复至正常状态;在此设定的参数下,两者相比,减少恢复时间比增大缓冲时间能更加快速有效地促进系统的恢复。 图9 故障情景2介质扰动系统状态函数图像 图10 故障情景3/4介质扰动系统状态函数图像 设定TD=2,绘制出各节点缓冲或恢复时间参数-扰动持续时间的函数关系图如图11所示。从图11可见,不同节点对系统故障传播的敏感性不同,改变某些节点的时间参数不会影响系统扰动传播的时间,如改变节点3、4、5、6的缓冲时间和节点3、5的恢复时间,系统的扰动传播时间不变;而减少节点4、6的恢复时间,系统的扰动传播时间缩短,系统恢复加快。 图11 介质扰动系统节点恢复时间或缓冲时间-扰动传播时间函数图像 (1)基于IRML语言提出了一种定性定量相结合的多层次故障传播模型。模型分为静态分析模块和动态分析模块,前者静态分析石油加工复杂系统故障传播结构特征,后者通过故障情景模拟,动态分析石油加工复杂系统的故障演化机理。 (2)多层次故障传播模型不仅能够分析油气加工系统故障传播的结构特征,而且能定量地描述多工况、多故障模式下的故障传播特征。 (3)以常减压蒸馏系统为例进行多层次故障传播建模。分别依据实际的工艺流程和工况条件确定模型中的结构图和参数设置,得到的结果可靠有效,符合实际的故障传播情况。因此,多层次故障传播模型适用于油气加工复杂系统的故障行为研究。 (4)多层次故障传播模型与工艺流程模拟软件相结合,可进一步实现实时的动态故障行为建模,促进油气加工系统的故障趋势预测、故障溯源和系统柔性诊断等方面的研究。 [1] 陈明亮. 化工装置事故的多米诺效应定量分析关键问题研究[D].北京:北京化工大学,2013. [2] 何俊. 基于复杂网络理论的电力系统连锁故障分析[D].吉林:东北电力大学,2013. [3] 徐林. 石油化工中的风险评价[J].污染防治技术,2010,23(5):42-46.(XU Lin.The risk assessment in petrochemical industry[J].Pollution Control Technology.2010,23(5):42-46.) [4] 张卫华. 基于SDG的多种故障诊断方法融合的异常工况管理系统研究[D].北京:北京化工大学,2010. [5] 于洋,陈晓春. 结构化SDG-HAZOP建模方法[C]//2012管理创新、智能科技与经济发展研讨会论文集.凤凰:南昌工程学院经济贸易学院,2012:1198-1202. [6] JOHANSSON J, HASSEL H.An approach for modeling interdependent infrastructures in the context of vulnerability analysis[J].Reliability Engineering and System Safety, 2010,95:1335-1344. [7] HERRERA I A, WOLTIER R.Comparing a multi-linear (STEP) and systemic (FRAM) method for accident analysis[J].Reliability Engineering and System Safety, 2010,95:1269-1275. [8] BELMONTE F, SCHÖN W, HEURLEY L, et al.Interdisciplinary safety analysis of complex socio-technological systems based on the functional resonance accident model:An application to railway traffic supervision[J].Reliability Engineering and System Safety, 2011,96:237-249. [9] 赵劲松, 陈丙珍, 沈静珠.人工神经网络在动态过程故障诊断中的应用[J].石油学报(石油加工), 1996,16(1):85-94.(ZHAO Jinsong, CHEN Binzhen, SHEN Jingzhu.Artificial neural networks in dynamic process fault diagnosis[J].Acta Petrolei Sinica (Petroleum Processing Section), 1996,16(1):85-94.) [10] 吕翠英, 徐亦方, 沈复.石油精馏系统故障诊断专家系统中基于深层知识的学习模型——一种不完善理论问题的处理方法[J].石油学报(石油加工), 1993,9(4):28-34.( LÜ Cuiying, XU Yifang, SHEN Fu.Petroleum distillation system fault diagnosis expert system based on deep knowledge learning model——A kind of imperfect theory approach problems[J].Acta Petrolei Sinica (Petroleum Processing Section), 1993,9(4):28-34.) [11] FILIPPINI R, SILVA A.A modeling framework for the resilience analysis of networked systems-of-systems based on functional dependencies.Reliability Engineering and System Safety[EB/OL]. http://dx.doi.org/10.1016/j.ress.2013.09.010. [12] 王佳明. 基于复杂系统脆性理论的电网连锁故障预警模型研究[D].北京:华北电力大学,2013. Hierachical Fault Propagation Model for Petroleum Refining System Based on IRML MA Xi1,ZHANG Laibin1,HU Jinqiu1,CAI Zhansheng1,2 (1.Mechanical&StorageandTtransportationEngineeringDepartment,ChinaUniversityofPetroleum,Beijing102249,China;2.CNOOCZhongJiePetrochemicalCo.,Ltd,Cangzhou061101,China) As a continuous and integrated process consisting of diverse components, petroleum refining industry is a complex, non-linear, multivariate system. The fault behavior has characteristics of strong nonlinear and dynamic during fault propagation in petroleum refining system. The failure in one component can propagate to other components in a cascading manner. Hierarchical fault propagation model (HFPM) is proposed as an extension of the infrastructure resilience-oriented modeling language (IRML). The main contribution that consists in the design of HFPM is to analyze the structural and dynamicproperties of systems-of-systems during fault propagation. The analysis is of two types, static and dynamic. Static analysis deals with the degree components interact, i.e. structural feature. Dynamic analysis reveals the way fault propagates among components and system's resilience. The performance of the proposed model has been tested on an atmospheric and vacuum distillationsystem. Based on the results illustrated in this paper, HFPM can be used for fault propagation analysis in petroleum refining system and its modeling parameters can reflect structural feature and fault propagation behavior. Besides, HFPM can be further applied to the study on fault propagation trend prediction, fault tracing and system resilience in petroleum refining system. petroleum refining system; hierarchical fault propagation model; static analysis module; dynamic analysis module; fault propagation behavior; fault evolution 2014-04-29 国家自然科学基金(51104168)、教育部新世纪优秀人才支持计划(NCET-12-0972)、北京市自然科学基金(3132027)、中国石油大学(北京)科研基金(YJRC-2013-35)、北京市优秀博士学位论文指导教师科技项目(YB20111141401)资助 马曦,女,博士研究生,从事油气生产系统安全方面的研究;E-mail:seven7xi@126.com 1001-8719(2015)05-1193-10 P624.8 A 10.3969/j.issn.1001-8719.2015.05.024




2 案例分析




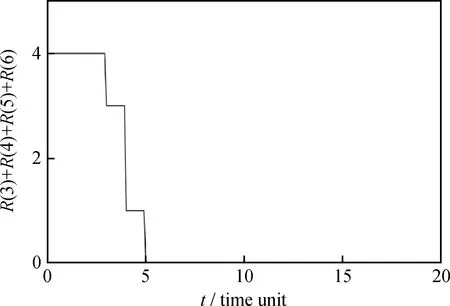
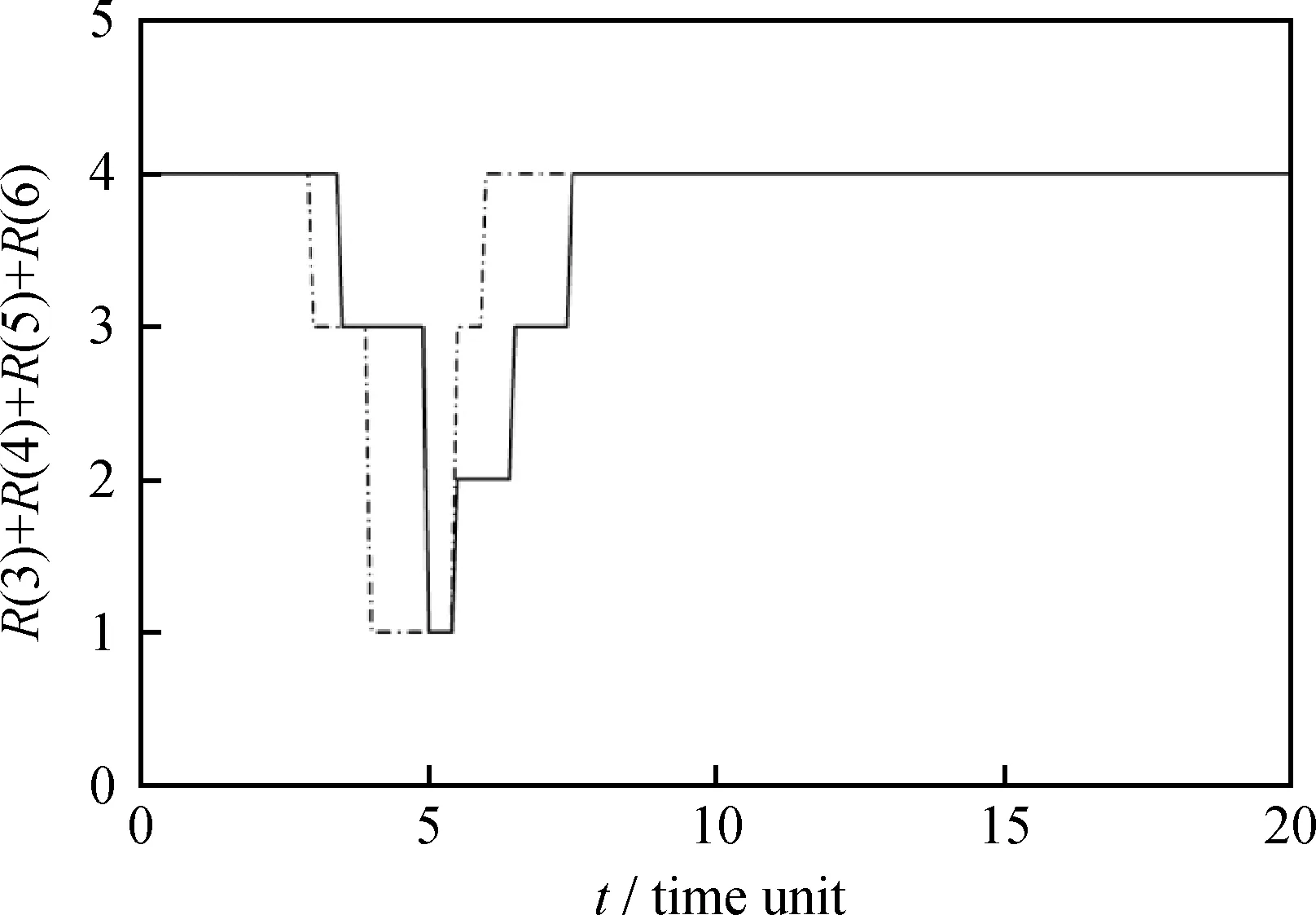
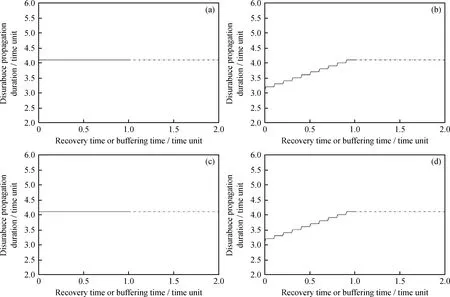
3 结 论

