径流年内分配不均匀性的度量指标及其应用

陆建宇，王秀庆，王学斌，陆宝宏

(1.河海大学水文水资源学院，江苏南京210098； 2. 淮河水利委员会沂沭泗水利管理局，江苏徐州221018；3.水资源高效利用与工程安全国家工程研究中心，江苏南京210098)

径流年内分配不均匀性的度量指标及其应用

陆建宇1，王秀庆2，王学斌3，陆宝宏1

(1.河海大学水文水资源学院，江苏南京210098； 2. 淮河水利委员会沂沭泗水利管理局，江苏徐州221018；3.水资源高效利用与工程安全国家工程研究中心，江苏南京210098)

河川径流的年内分配不均匀性直接影响水利工程的运行方式。为准确度量径流年内分配不均程度，尝试引入变率指数FI、分摊熵AE、基尼系数Gini、集中指数CI、余期望系数SEI和赫氏指数HHI等六种度量指标，并以沂河临沂站天然月径流为例，分析各指标的适用性及存在的不足。结果表明，各指标年际变化相似度极高，峰、谷值出现时间基本一致，可以使用其中的任何一个指标度量径流年内分配的不均匀性；Gini考虑了径流年内时程分布及各月径流量大小的影响，能够定量地评价径流年内分配的不均匀程度，比其他指标有更高的分辨力，用Gini度量径流年内分配不均匀程度最合适。

河川径流；年内分配；不均匀性；度量指标；沂河流域

河川径流变化分为径流“量”和“结构”的变化，径流年内分配特征指标分析属后者。即，从径流过程线的“形状”上反映年内不同时间上径流组分的分布状况[1]。近50年来，我国六大流域河川径流的年内分布发生了不同程度的改变，径流年内分配的变化必然给水资源管理、水库调度、农业以及水生生态系统带来一系列的影响[2- 4]。为此，量化分析径流的“结构”变化有现实意义。

目前，常用的径流年内分配特征量化指标主要包括集中度Cn[1，5- 6]和集中期D[5- 6]、不均匀系数Cu[1，5- 7]、完全调节系数Cr[5- 8]、相对变化幅度Cm[2，5]和绝对变化幅度ΔR[2，6]。总体而言，对径流年内分配的研究，仍然沿用传统的表示方法，多以单一方法或指标，若采用年内丰、枯水期或季节或特定时段的径流量占年径流量比值的方式表示，有时也可获得相同的效果，这不仅掩盖了相关方法或指标的优势，难以全面反映径流年内分配特征，还不能满足各方面对河川径流年内分配的要求[9]。鉴于此，本文尝试引入几种年内分配不均匀程度衡量指标，用实例计算分析探讨其在衡量径流年内分配不均匀性方面的可行性和适用性，以期为合理地量化径流年内分配不均匀性提供一种新途径。

1 指标原理及计算方法

1.1 变率指数

变率指数FI(Flashiness Index)是由Backer[10]等人于2004年提出的，用于描述河流径流变化程度的强弱，该指标适用于径流年内变化特征分析，可对逐月时段径流量进行描述。即

(1)

式中，ri为第i个月径流量；R为全年径流总量。FI值介于 0～2之间[11]。FI=0时，年内径流量无变化；FI值越大，径流波动越剧烈。

1.2 分摊熵

分摊熵AE(Apportionment Entropy)[12]主要用于度量降水年内分布的不均匀性。现尝试将其用于刻画径流年内分配不均匀性，即

(2)

式中，ri为第i个月径流量；R为全年径流总量。AE取值范围为0～log212[13]。为方便各指标间相互比较，这里采用的AE值为log212与原始AE的差值。AE=0时，年径流均匀分配在12个月内；AE=log212时，年径流全部集中在某一个月内。AE值越大，径流的年内分配越不均匀。

1.3 基尼系数

基尼系数Gini(Gini coefficient)是一个衡量居民内部收入分配差异程度的指标，实质是对分布均匀度的量化分析，王波雷[14]将其用于分析乌兰木伦河径流年内分布均匀度，其原理与计算方法见文献[9，14]。

Gini取值介于0到1[9]。Gini值在0.2以下，径流年内分配绝对平均；0.2～0.3之间，相对平均；0.3～0.4之间表示比较合理；0.4～0.5差距偏大；0.5以上为高度不平均。Gini值越小，径流年内分配越均匀；反之，则越不均匀。

1.4 集中指数

集中指数CI(Concentration Index)是由Oliver[15]于1980年提出的，被用于研究降雨侵蚀力的年内变化特征[16]，现将其引入到径流年内分配分析中。其计算公式

(3)

式中，ri为第i个月径流量；R为全年径流总量。CI取值介于8.33～100。当CI=8.33时，年径流均匀分配在12个月内；8.3320时，径流月际变化显著；CI=100时，径流全部集中在1个月内。

1.5 余期望系数

余期望系数SEI(Surplus-Expectation Index)是一种反映收入差异程度的新指标[17]。该指标不涉及不规则图形面积的计算，不同时间、不同空间的系数值可以直接对比。根据余期望系数的特点，现将其用于分析径流年内分配的离散程度，即

SEI=1+[(∑PilnPi)/ln12]

(4)

Pi=ri/R

式中，ri为第i个月径流量；R为全年径流总量；Pi为第i个月径流量占年径流总量比例。SEI取值介于0～1之间，其值愈靠近0，径流年内分配愈均匀；其值愈靠近1，径流年内分配愈不均匀。

1.6 赫氏指数

赫芬达尔-赫希曼指数HHI(Herfindahl-Hirschman Index)，简称赫氏指数，是一种市场集中度的综合指标[18]，兼有绝对集中度和相对集中度指标的优点。现将其用于度量径流年内分配的离散程度，即

(5)式中，ri为第i个月径流量；R为全年径流总量；Pi为第i个月径流量占年径流总量比例。HHI取值为1/12～1。HHI=1/12时，径流均匀分配在12个月内；HHI=1时，年径流集中在1个月内。HHI值越大，年内分配越不均匀；反之，则年内分配越均匀。

1.7 不均匀系数

不均匀系数Cu(Unevenness Coefficient)又称变差系数，是反映时间序列分配不均匀程度的一个综合性指标，能用于多种性质的时间序列的分析研究[7]。Cu因其具有良好的时间空间可比性，在我国得到了广泛应用。其计算公式为

(6)

2 不均匀性度量指标应用

2.1 研究区及资料

研究资料为沂河临沂站1953年～2000年共48a的天然月径流序列。沂河发源于山东省沂蒙山南麓，属暖温带半湿润季风气候区。临沂水文站是沂河主要控制站，临沂站以上为山丘区，河道长223 km，水系大致呈扇形，集水面积为10 315 km2，占全流域面积的87.3%[6]，在山东半岛具有一定的代表性。

2.2 径流年内分配情况

图1为临沂站天然径流各年年内分配比例。由图1可看出：①天然径流在各年代年内均呈不对称的单峰型分布，1月～5月、9月～12月径流量相对较小，且变化平缓；6月份径流增加，多于7月、8月份达到峰值；②径流年内主要集中分配在6月～10月。其中，最大月径流量在7月或8月，占年径流量的32.92%～43.23%；最小月径流量在2月或3月，占年径流量的1.05%～1.43%。

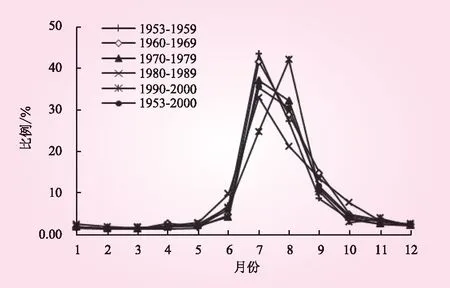
图1 临沂站天然径流年内分配过程及年内分配比例

2.3 径流年内分配不均匀性分析

图2为临沂站天然径流FI、AE、Gini、CI、Cu、SEI和HHI值年际变化过程；表1为临沂站天然径流年内分配各指标年际变化特征值统计。

表1 临沂站天然径流年内分配不均匀性度量指标特征值统计

由图2和表1可得：①FI、AE、Gini、CI、Cu、SEI和HHI多年平均值分别为0.879、1.11、27.686、0.550、1.463、0.312和0.277。其中，Gini值显示径流年内分配高度不平均，CI值表明径流年内月际变化显著。②各指标年际变化相似度极高，各指标峰、谷值出现时间基本同步，当出现1957、1960、1970、1974、1991和1997年洪水时，各指标数值都比较大，其中各指标年际最大值均出现在1957年，该情况是由年内7月6日到26日发生7次极端暴雨，汛期流量比重严重偏大所致[19]；流域出现1959、1968、1969、1984和1989年干旱时，各指标都比较小。其中除FI外，其他指标年际最小值均出现在1968年，恰与年内汛期降水量严重偏少符合。③就极值比值和变差系数来看，AE和SEI的极值比值、差系数，其变化范围与离散程度均较大，对径流年内分配不均匀程度的区分效果相对明显。

2.4 径流不均匀性度量指标适用性分析

2.4.1 归一化处理及相关性分析

不同指标的取值范围并不相同，很难绘制到同一坐标系下，不利于评价比较，而归一化方法能够消除各指标取值与量纲差异的影响，为所有指标树立一个统一的标准。本次采用零一均值归一化法[20]，即

(7)

图3为各指标归一化后的年际变化过程线，表2为各指标的归一化值相关性检验表。

由图3和表2可以看出：①各指标的年际变化相似度极高，各指标峰、谷值出现时间同步，能够与流域汛期洪水、干旱发生时间很好对应，且与前述分析结果完全一致；②FI、AE、Gini、CI、Cu、SEI和HHI归一化值间的相关系数均通过了0.01的显著性水平检验，各指标间存在显著的正相关性。其中，CI与HHI、AE与SEI的相关系数达1.000，其计算结果的变化规律完全一致。不难看出，各指标的极值出现时间及变化规律高度一致，在度量径流年内分配不均匀性时，可使用其中任一指标，但各指标又不能完全相互替代。

图2 临沂站天然径流年内分配不均匀性度量指标年际变化过程线

2.4.2 各指标存在的不足及改进

径流不均匀性度量指标可分为绝对指标和相对指标两类。变率指数、分摊熵、基尼系数、集中指数、余期望系数、赫氏指数和不均匀系数均属于相对指标，各指标的大小与度量单位无关，能够相对准确地体现径流年内分配不均匀程度。

FI、AE、Gini、CI、Cu、SEI和HHI的年际变化及归一化后的相关性分析显示，各指标有近乎一致的变化规律，各指标物理意义不同，需结合其公式特点做进一步分析。从各指标的计算公式上不难看出：①AE、CI、SEI和HHI均以各月径流量占年总径流量的比例为输入，对径流量较大的月份所占年总径流的份额更加敏感，能定性地体现大流量月份对径流年内分布的影响程度；其中，CI能够定量刻画径流年内分配的不均匀程度，而AE、SEI和HHI只能定性表示，因而CI的分辨力较AE、SEI和HHI高。②Cu反映年内各时段径流偏离时段平均径流的程度，其物理概念明确、适用性强，但其时段平均径流量易受年际及年内极端值的影响，仅能定性的表达径流年内分布不均匀程度。③FI通过计算径流年内改变量的累积百分比来定性地描述径流年内分配不均匀程度，对极值点的刻画并不和其他指标一致。④Gini比其他指标有更高的分辨力，这一点从Gini的计算原理得到证实。Gini采用水文要素月径流值按时序排列，并进行逐时段累加的升序排列方法，既考虑了径流年内排序的影响，又兼顾了各月径流量的大小差异，在描述径流年内分配不均匀程度方面具有更高的准确性。

图3 临沂站天然径流年内分配指标归一化值年际变化过程

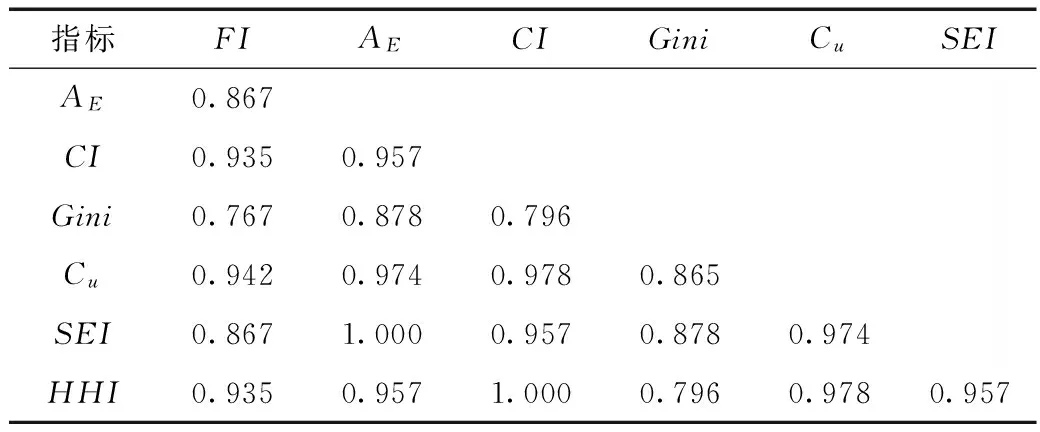
指标FIAECIGiniCuSEIAE0.867CI0.9350.957Gini0.7670.8780.796Cu0.9420.9740.9780.865SEI0.8671.0000.9570.8780.974HHI0.9350.9571.0000.7960.9780.957

注：自由度 n=48对应显著性水平a=0.01时，ra=0.369。

总体来讲，只要径流年内组成不同，就会得到不同的Gini、FI，而AE、CI、SEI、HHI和Cu则不同。尽管各月流量大小不变，但若年内各月时程分布不同，AE、CI、SEI、HHI和Cu值并不会变化，说明AE、CI、SEI、HHI和Cu对年内径流分配的敏感性不如Gini、FI高。考虑到FI对极值点的刻画和其他指标有所差异，用Gini分析径流年内分配不均匀程度更为合适，并可尝试将其用于其它水文要素年内分配不均匀性的定量描述。另外，针对AE、CI、SEI、HHI和Cu在径流年内分配不均匀性方面存在的不足，建议缩小输入数据的尺度，如以旬径流量取代月径流量，以弥补各指标在径流年内时程分布上考虑的不足，提高度量径流年内分配不均匀程度的准确性。

3 结 论

分析河川径流年内分配不均匀程度，不仅有助于深入了解流域水资源的年内分布特性，还可为流域水资源合理开发、利用提供一定的参考依据。本文尝试引入几种新指标，以沂河临沂站天然月径流为输入，分析了各指标的年际变化规律及适用性，发现在度量径流年内分配不均匀性时，可使用上述任何一个指标。由于各指标的物理意义不同，其计算表达式存在一定的差异，致使各指标均存在一些不足。在分析径流年内分配不均匀性时，建议参考各指标的优缺点，从不同的分析角度和目的来选取最合适的指标，并尽量缩小输入数据的尺度，以弥补各指标对径流年内时程分布上考虑的不足；从而更加准确地度量径流年内分配不均匀性。

[1]涂新军， 陈晓宏， 张强， 等. 东江径流年内分配特征及影响因素贡献分解[J]. 水科学进展， 2012， 23(4)： 493- 501．

[2]郭巧玲， 杨云松， 畅祥生， 等. 1957- 2008年黑河流域径流年内分配变化[J]. 地理科学进展， 2011， 30(5)： 550- 556．

[3]张秀菊. 水电站保证出力的计算方法[J]. 水力发电， 2006， 32(10)： 21- 23．

[4]LU B H， GU H H， XIE Z Y， et al. Stochastic simulation for determining the design flood of cascade reservoir systems[J]. Hydrology Research， 2012， 43(1/2)： 54- 63．

[5]孔兰， 陈俊贤. 多沙河流水沙年内分配特征研究[J]. 水力发电， 2012， 38(6)： 12- 15．

[6]陆建宇， 陆宝宏， 朱从飞， 等. 沂河流域天然径流变化规律分析[J]. 中国农村水利水电， 2014， (7)： 67- 71．

[7]周成虎， 汤奇成. 水文时间序列不均匀系数的分析与计算[J]. 自然资源， 1989(8)： 39- 44．

[8]吕琳莉， 尼玛次仁， 王维成， 等. 尼洋河流域径流时空变化特性初步分析[J]. 水力发电， 2011， 37(2)： 5- 7．

[9]胡彩霞， 谢平， 许斌， 等. 基于基尼系数的水文年内分配均匀度变异分析方法- 以东江流域龙川站径流序列为例[J]. 水力发电学报， 2012， 31(6)： 7- 13.

[10]BAKER D B， RICHARDS R P， TIMOTHY T， et al. A new flashiness index： characteristics and applications to midwestern rivers and streams[J]. Journal of the American Water Resources Association， 2004， 40(2)： 503- 522．

[11]黄金良， 张祯宇， 邵建敏， 等. 九龙江径流 Flashiness 指数时空变化分析[J]. 水文， 2014， 34(3)： 37- 42．

[12]KAWACHI T， MARUYAMA T， SINGH V P. Rainfall entropy for delineation of water resources zones in Japan[J]. Journal of Hydrology， 2001， 246(1- 4)： 36- 44．

[13]周文婧， 夏自强， 黄峰， 等. 巴尔喀什湖流域降水量及其年内分配的变化特征[J]. 水电能源科学， 2013，31(6)：10-13．

[14]王波雷， 马孝义， 张建兴. 乌兰木伦河径流分布均匀度及其变异点研究[J]. 水力发电， 2008， 34(8)： 4- 7．

[15]Oliver J E. Monthly precipitation distribution： a comparative index[J]. Professional Geographer， 1980， 32(3)： 300- 309．

[16]郭青霞， 陈焕伟. 大同市降雨侵蚀力时间变化特征分析[J]. 中国水土保持科学， 2006， 4(5)： 25- 29．

[17]尚卫平. 一种反映收入差异程度的新指标—余期望系数[J]. 统计研究， 2004(1)： 35- 37．

[18]JURAJ P， ANNA O， IVAN B. Analyses of Absolute Concentration of the Selected Branch by Herfindahl-Hirschman Index[J]. Journal of Economics， 2009(1)： 77- 94．

[19]沂沭泗水利管理局. 沂沭泗防汛手册[M]. 中国矿业大学出版社， 2003．

[20]李树忱， 冯现大， 李术才， 等. 矿井顶板突水模型试验多场信息的归一化处理方法[J]. 煤炭学报， 2011， 36(3)： 447- 451．

(责任编辑 陈 萍)

Measure ment Index of Nonuniformity of Intra-annual Runoff Distribution and Its Application

LU Jianyu1, WANG Xiuqing2, WANG Xuebin3, LU Baohong1

(1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, Jiangsu, China; 2. Water Conservancy Administration of Yi-Shu-Si River Basin of the Huaihe River Commission, Xuzhou 221018, Jiangsu, China; 3. National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Nanjing 210098, Jiangsu, China)

The nonuniformity of intra-annual stream flow distribution has a direct impact on water projects’ operation mode. In order to measure the nonuniformity of intra-annual stream flow distribution accurately, six measure ment indexes are introduced, including Flashiness Index (FI), Apportionment Entropy (AE), Gini coefficient (Gini), Concentration Index (CI), Surplus-Expectation Index (SEI) and Herfindahl-Hirschman Index (HHI). The applicability and disadvantages of these indexes are obtained through the natural monthly runoff data of Linyi Station in Yihe River Basin. The results show that: (a) there is a high degree of similarity about the inter-annual variability of each index and the appearance time of peak, valley points are almost the same, so any one of which can be used as an indicator to measure the nonuniformity of intra-annual stream flow distribution; (b) the temporal distribution of intra-annual stream flow and the size of the monthly runoff are considered in Gini and Gini can quantitatively evaluate the nonuniformity of intra-annual stream flow distribution, so the Gini has a higher resolution than other indexes and is the most appropriate index to measure the nonuniformity of intra-annual stream flow distribution．

stream flow; intra-annual distribution; nonuniformity; measure ment index; Yihe River Basin

2014- 10- 28

国家自然科学基金资助项目(50979023)；水利部公益性行业科研专项经费项目(201201026)

陆建宇(1989—)，男，内蒙古赤峰人，硕士研究生，研究方向为水资源规划与管理．

TV121

A

0559- 9342(2015)11- 0024- 05