悬链线的几何特征

邱为钢

（湖州师范学院理学院，浙江 湖州 313000）

质量均匀分布的绳子，两端固定，在重力场中重力势能最小的绳子位形，就是悬链线[1，2].文献[2]讨论了悬链线几何形状与外力作用形式的联系.本文的悬链线模型，绳子两端在同一水平线上，外力只有重力和绳子最底端悬挂重物施加的拉力，这相当于文献[2]中外力分布函数为连续分布叠加一个单点的离散分布.悬链线两端的水平距离定义为宽度2D，两端连线到绳子最低点的垂直距离定义为高度H，如图2所示.半宽度D和高度H就是悬链线的几何特征.实验中发现，半宽度D变大，高度H则变小，反之亦然.物理现象研究的问题之一就是找出两个变化物理（或者几何）量所隐含的关系.即，悬链线的几何特征、宽度和高度满足什么样的关系式？

1 理论推导

首先利用微元分析法来推导悬链线方程，设悬链线的长度是2l，线密度是ρ.由对称性，设悬链线的最低点为原点，最低点悬挂重物，其质量为m.弧长坐标在（s，s＋ds）的绳子微元受到3个力：两端的张力，大小分别为T（s）和T（s＋ds），重力G＝ρgds，如图1所示.

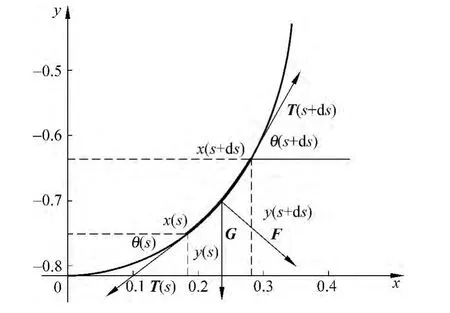
图1 绳子微元受力分析示意图

绳子微元受力平衡，分解为水平和竖直方向，得到

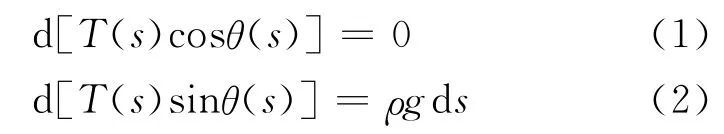
其中，θ（s）是弧长坐标s处悬链线切线与水平方向的夹角，且有

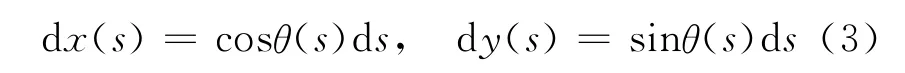
悬链线最低点重物受力平衡，有

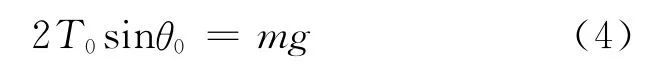
其中，T0是悬链线最低端的张力；θ0是悬连线最低端切线与水平方向的夹角，m是重物质量.由式（1），式（2）和式（4）解得

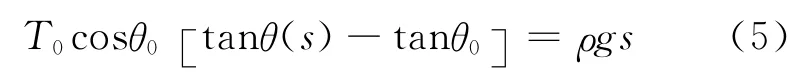
作变量代换tanθ＝sinhτ，这样有cosθ＝1／coshτ，sinθ＝tanhτ.设τ0是绳子最底端对应的参数，τ1是绳子其中一个端点（不妨设为右端）对应的参数.把式（5）代入式（3），计算得到悬链线形状的参数方程

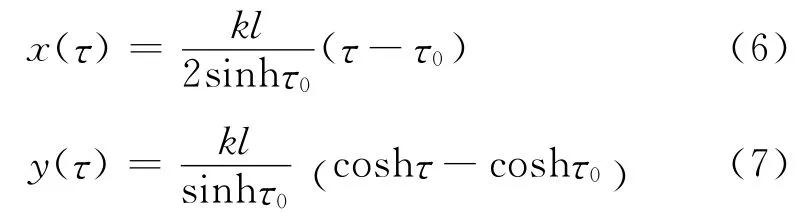
其中比例系数k是重物质量m与悬链线质量的比值，与参数τ1，τ0的关系式为

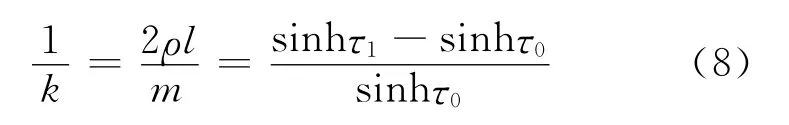
由式（6）和式（7）得到悬连线的半宽度D和高度H为

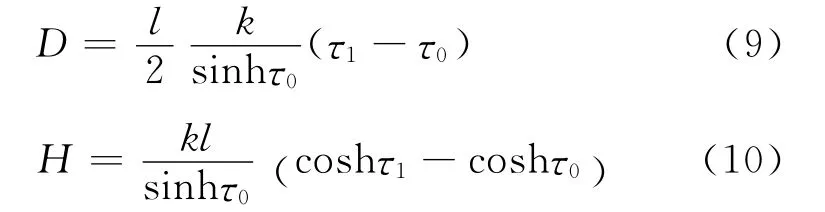
式（9）、式（10）就是悬链线半宽度D和高度H的参数方程.

接下来讨论两个极限，一个是不挂重物，此时k＝0和τ0＝0，悬链线形状方程为

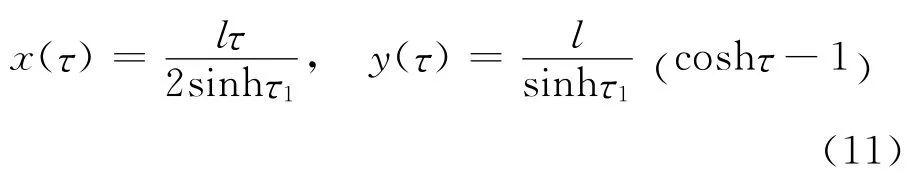
另一个是重物质量为无穷大，相当于链子质量为零，很容易看出悬链线形状为V字形的两个线段.

2 实验验证

实验中所用的链子长度是66cm，质量是17.706g.悬挂重物（砝码）分别为2g，5g和10g.宽度固定为16，20，24，28，32，36，40cm.实验实物图和悬链线宽度2D和高度H标注如图2所示.

图2 实验实物图和悬链线宽度2 D和高度H 标注图

实验测得悬链线高度H（单位cm）数据如表1所示.

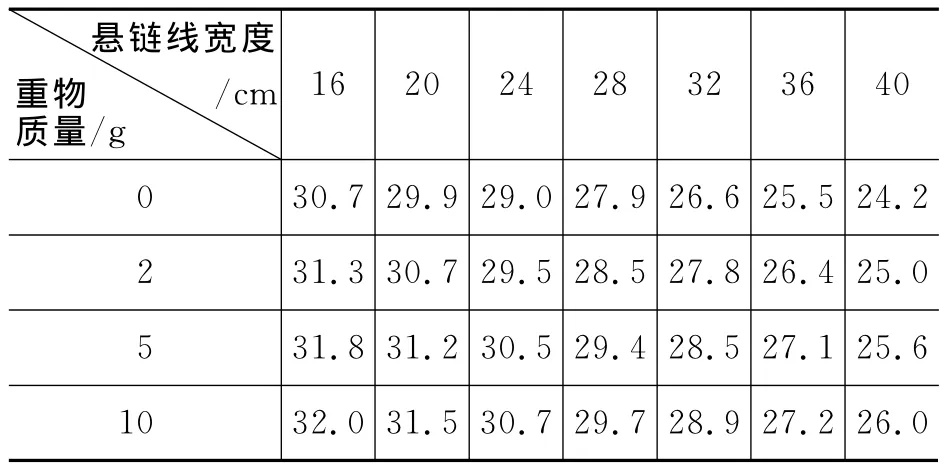
表1 悬挂不同重物时悬链线高度H与宽度2D数据表

根据表1的数据和理论公式（9）、（10），我们得到以下4个悬链线高度H和半宽度D的关系图（图3～图6），其中实线是理论曲线，三角形标记是实验数据.

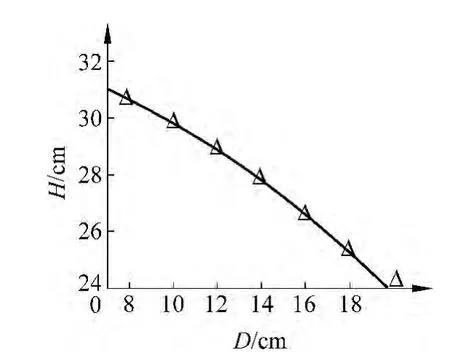
图3 m＝0g高度与宽度关系图

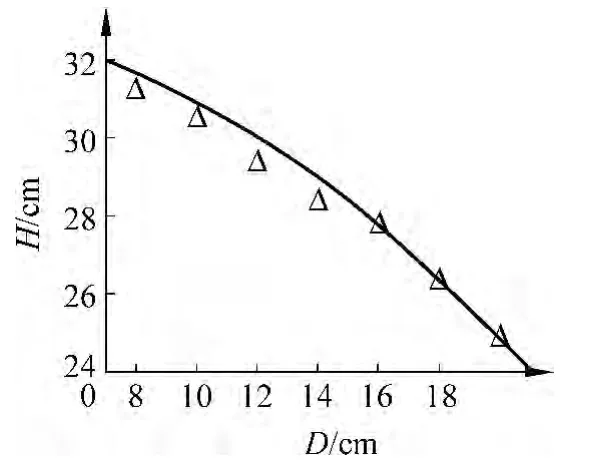
图4 m＝2g高度与宽度关系图

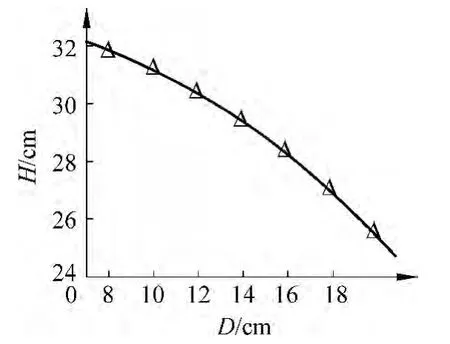
图5 m＝5g高度与宽度关系图

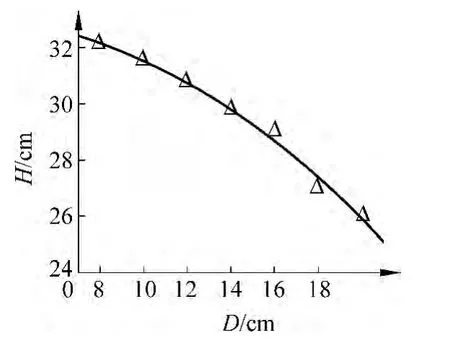
图6 m＝10g高度与宽度关系图

3 结语

对称悬链线最明显的几何特征就是它的高度和宽度，这在实验上很容易测量和调节.悬链线最底端也可以悬挂重物，这又可以增加一个可以调控的参量.实验中得到了悬链线高度和宽度的数据，这些数据落在哪条理论曲线附近，就对该理论分析进行验证.我们使用最简单的模型，绳子质量均匀分布，绳子微元受力平衡，得到微分方程组.利用变量代换，得到了绳子坐标与参量的明确表示式，进而得到了悬链线宽度D和高度H的参数方程.实验数据基本落在理论曲线附近，说明我们的模型建立和理论推导是基本正确的.

[1]于凤军，崔金玲，李立新.利用平衡原理导出悬链线方程[J].物理与工程（原名工科物理），1998，8（4）：14-16.

[2]李玉良，黄湘茹.匀质悬链几何形状的力学研究[J].物理与工程，2013，23（1）：8-10.