牛顿环实验最佳方法的对比
曹佳妍 顾菊观 苏婷燕
(湖州师范学院理学院,浙江 湖州 313000)
牛顿环干涉实验是大学物理实验中一个重要的基础性实验,基本实验方法是通过读数显微镜对牛顿环的干涉条纹进行测量,进而计算出平凸透镜的曲率半径[1,3,4].在计算方法的选取上,文献[2,5~10]讨论了逐差法计算方法和不确定度的计算及评定,但是并没有比较直径方法和半径方法等.在数据处理方面有应用C语言和Origin软件进行计算和处理得到平凸透镜曲率半径[7,12-15].本文将通过比较直径计算的两种逐差法,得到最佳测量方法和最佳计算方法;再结合Mathematics进行最小二乘法作图求得平凸透镜的曲率半径,比较理论计算和数据拟合得到的曲率半径得出最佳数据处理方法.该讨论和比较为牛顿环实验测量、计算和数据处理提供了很好的指导.
1 直径逐差后平均法
测量牛顿环条纹暗环的直径,由公式(1)应用逐差后平均法计算平凸透镜的曲率半径:
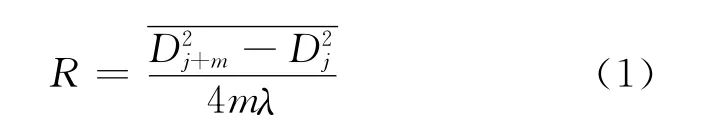

图1 测量牛顿环干涉条纹示意图
在测量过程中,选取环数为1~50暗环进行测量,测量方法如上所述,每环暗纹测量3次.所有值的单位为mm,测量结果见表1(因篇幅有限,只提供前20环的数据).表1的第3、5、7列是以式(1)计算所得的平凸透镜曲率半径,表1的第8列是每个暗纹3次测量直径的平均值,第9列是以下面式(3)计算所得的平凸透镜曲率半径.
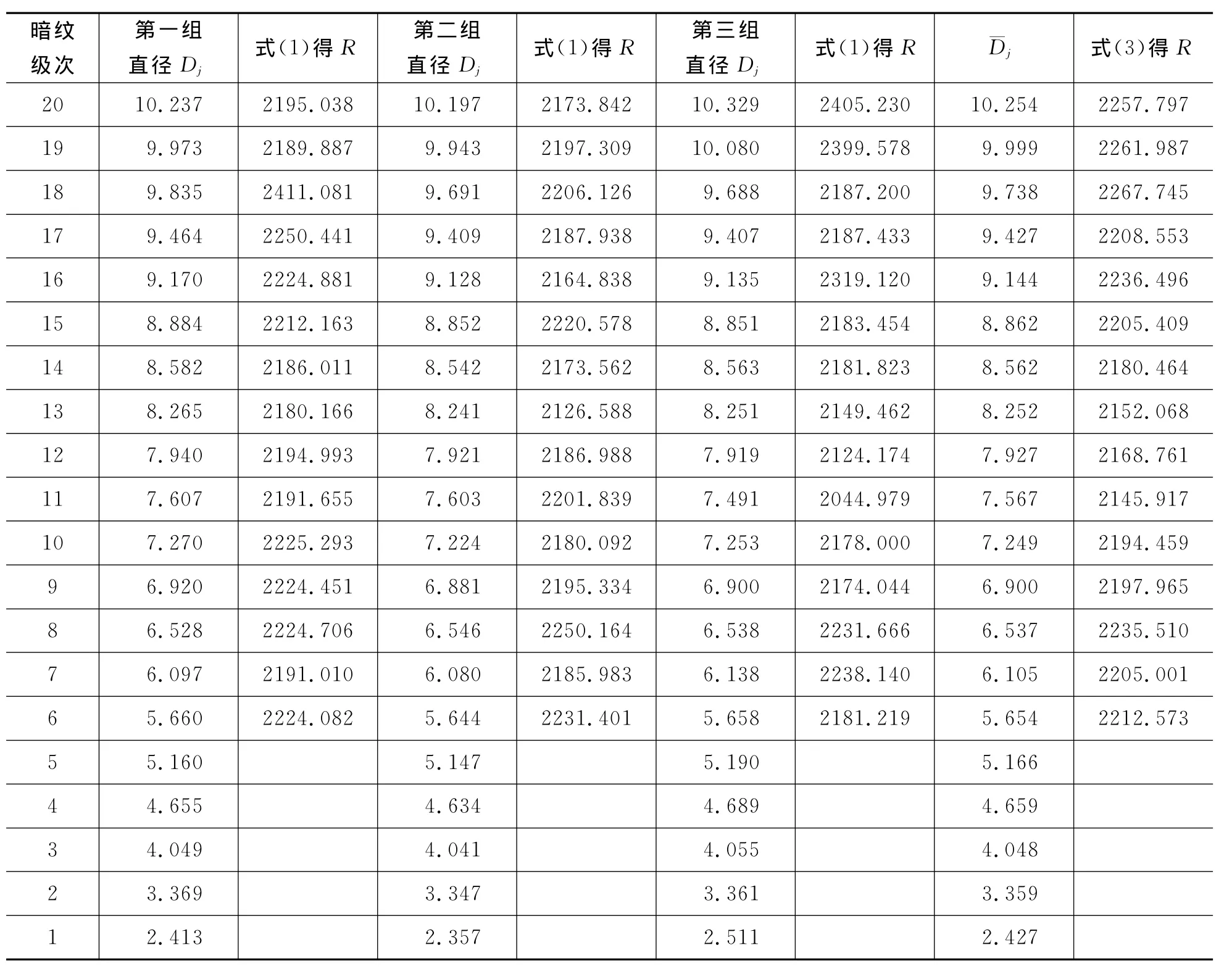
表1 每组暗纹直径和平凸透镜的曲率半径
曲率半径对应的不确定度公式[16]为
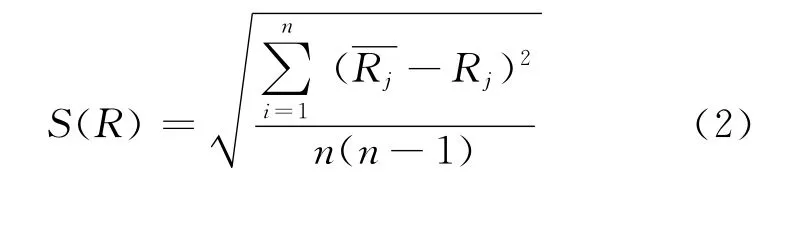
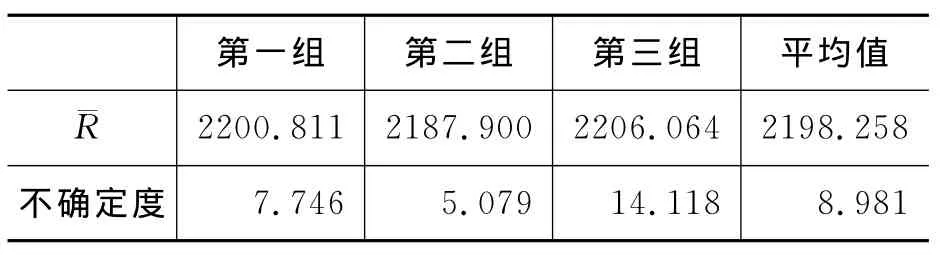
表2 各组曲率半径的平均值和不确定度
由表2知,第三组测量数据与前二组相差很大,说明测量时肯定有较大的偶然误差存在,该数据不予考虑.考虑前二项的结果,=2194.356mm,S(R)=6.413mm.
2 直径平均后逐差法
测量条纹暗环的直径,先算出直径的平均值,再求平均值的平方差后代入式(3)得到R
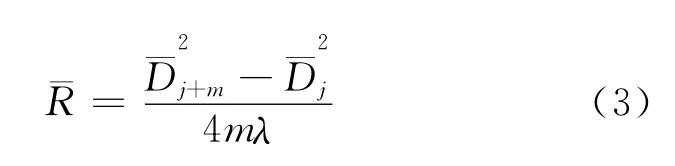
最后再求平均(其中m=5).测量方法与逐差后平均法相同.测量和计算结果见表1,由表1第9列得,

3 数据拟合
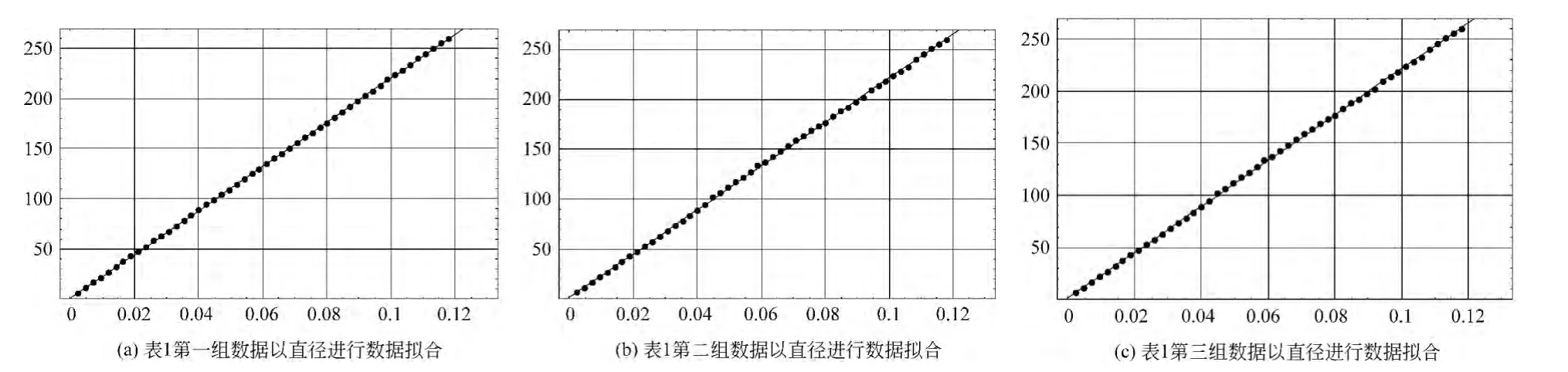
图2 以暗纹直径数据拟合得曲率半径
图2(a)拟合得到的一次函数y=2198.08x+1.07,即平凸透镜的曲率半径=2198.08mm;图2(b)拟合得到的一次函数y=2198.19x+0.39,即平凸透镜的曲率半径=2198.19mm;图2(c)拟合得到的一次函数y=2199.71x+1.51,即平凸透镜的曲率半径=2199.71mm.以表1数据实验理论计算与数据拟合得到的曲率半径比较见表3,由表3知数据拟合得到的结果比实验理论计算得到的结果的不确定度要小很多,其结果与文献[11,13~15]相一致.因而,实验过程中可以选择数据拟合和实验理论计算来计算平凸透镜的曲率半径,在精度要求不高时两者都可以,但应用计算机处理数据计算方便和省时,计算结果的不确定度较小,因而建议使用计算数据拟合来进行数据处理和计算比较好.
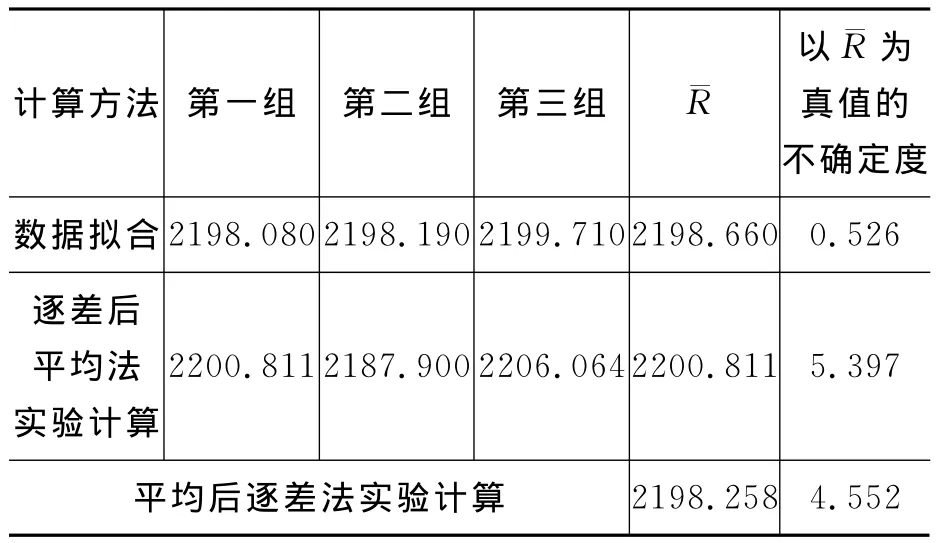
表3 以直径方法进行数据拟合结果与实验理论计算结果比较
4 结语
牛顿环干涉实验中测量直径是最佳测量方法,以平均后逐差法计算是最佳计算方法,以数据拟合进行数据处理是最佳处理方法,3个方法综合应用所得结果不确定度最小,因此,建议牛顿环干涉实验中要想得到最佳结果需要满足以上3个最佳.上述方法对培养学生的动手能力、数据处理能力和计算应用能力是很有效的;在学生实验时间足够和学生开放实验时,可以让学生尝试多种实验测量方法和数据处理方法进行实验对比,对学生科学思想、科学方法和科学素质培养是很有益的途径之一.数据处理和曲线拟合也可应用Matlab和Excel等软件进行处理.
[1]杨述武.普通物理实验(光学部分)[M].北京:高等教育出版社,2000.
[2]赵纪平,徐庆强.牛顿环实验数据处理的最佳方法[J].徐州师范大学学报(自然科学版),2001,19(4):48-50.
[3]腾敏康.实验误差与数据处理[M].南京:南京大学出版社,1989.
[4]任隆良,谷晋骐.物理实验[M].天津:天津大学出版社,2009.
[5]李平.牛顿环实验的三种数据处理方法物理实验[J].物理实验,1989,11(3):115-117.
[6]虞仲博,屠全良.牛顿环实验等精度测量及其不确定度的评定与表示[J].物理实验,2000,20(5):17-19..
[7]苗琦,王明东,等.牛顿环测透镜曲率半径数据分析和结果探讨[J].物理与工程,2010,20(5):32-33,57.
[8]刘长发.牛顿环实验方法的改进[J].物理与工程,2006,16(1):34-36.
[9]王雅红.不同数据采集方法对牛顿环测曲率半径准确度的影响[J].物理与工程,2005,15(4):36-38.
[10]李平.牛顿环实验数据处理方法的回顾与讨论[J].物理与工程,2002,12(12):31-33,62.
[11]谭亮,高雄健,等.C语言和Origin7.5软件在实验中的应用[J].物理通报,2013,23(1):77-80.
[12]滕坚.牛顿环实验数据处理方法分析[J].物理通报,2006(6):34-36.
[13]唐春红,唐曙光,刘扬正.逐差法和Origin8.0软件在牛顿环实验数据处理中的比较[J].物理通报,2013(9):98-100.
[14]苗琦,王金苗.Origin软件在牛顿环测透镜曲率半径实验数据处理中的应用[J].大学物理实验,2011,24(2):76-78.
[15]王晓雄.利用Origin拟合方法处理牛顿环实验数据[J].大学物理实验,2011,24(4):73-74.
[16]陈殿伟,盖啸尘,等.牛顿环实验测量结果不确定度的评定[J].大学物理实验,2007,20(3):72-74.

