基于M/M/n排队系统的公厕性能研究

王先超，盛乐园，董书一，成红梅，于 勤

(1.阜阳师范学院 数学与统计学院，安徽 阜阳 236037；2.蚌埠三十一中，安徽 蚌埠 233000)

基于M/M/n排队系统的公厕性能研究

王先超1，盛乐园1，董书一2，成红梅1，于 勤1

(1.阜阳师范学院 数学与统计学院，安徽 阜阳 236037；2.蚌埠三十一中，安徽 蚌埠 233000)

针对公厕排队问题，本文基于M/M/n排队系统建立公厕排队模型，并通过仿真分析了传统的男女分离公厕和无性别公厕排队系统的性能。结果显示无性别公厕的各项性能指标都优于传统公厕，从而为解决公厕排队问题提供解决思路和理论依据。

排队论；无性别公厕；M/M/n排队系统

在一些人口密集的地方如旅游景区、超市商场、影剧院、候车候机厅、交通枢纽等公共场，频频出现公厕排队的现象，尤其是女厕，引发了许多学者的共同关注。其中柏文学提出应该为妇女提供公平的公共厕所的如厕权[1]。我国现在大型公共场所的公厕都是实行男女分开的策略，男女使用设施(包括蹲位和小便器)比例一般为1∶1。由于生理和着装的原因，如厕时女性有着比男性更复杂的要求，而出现了男性基本无需等待、女性则要排队等待时间很长的现象。其原因归根到底就是公厕男女设施数量配比标准不合理或使用策略不当。为解决该问题，在《城市公共厕所设计标准》中，特别强调：“厕所男蹲(坐、站)位与女蹲(坐)位的比例宜为 1∶1～2∶3”。马康丁认为男女所用设施应为1∶2[2]。夏苏湘认为若如厕的男、女人数相等，则男女所用设施需求比例为1. 0∶2. 6，其中男性蹲位与小便器的比例约为1∶2[3]。管羚雅等认为男女公厕的蹲位比理论的合理值应该是1∶2.2[4]。但现实生活中由于种种原因，并非如此。邹茜、石之光认为增加公厕的数量是解决公厕排队问题的一项非常重要措施[5-6]。然而，这些解决公厕排队问题的方法基本都缺少相关理论和性能分析。

作为随机运筹学中重要学科的排队论，经历了一百多年的发展历程，已广泛应用于解决通信[7]、运输[8]、库存[9]、任务调度[10]、资源分配[11]等诸多领域问题，凸显了其强大生命力。本文拟基于M/M/n排队系统建立传统男女分离公厕和无性别公厕的排队模型，并对其性能进行分析与比较。

1 基于M/M/n排队系统的公厕排队模型

针对公厕排队现象，为提高两性对公共设施使用公平性，促进公厕合理化建设和使用，本文基于M/M/n排队系统[12-13]建立公厕排队模型。图1(a)和(b)分别为传统公厕和无性别公厕排队模型。

为研究系统性能，作如下假设：

男厕和女厕各有n个服务设施，且各设施的服务是相互独立的；

男女顾客均按泊松流到达，到达强度均为λ，则无性别公厕顾客到达强度为2λ；

女厕各设施服从平均服务率为μ的负指数分布，其平均服务率为nμ。

由文献[14]可知男女如厕耗时之比为1∶2，则男厕各设施服从平均服务率为2μ为负指数分布，其平均服务率为2nμ。

在相同数量服务实施的条件下，无性别公厕共有2n个服务实施，各设施服从平均服务率为1.5μ的负指数分布，其平均服务率为2n×1.5μ=3nμ。

图1 公厕排队模型示意图

显然，无论是男厕、女厕还是无性别公厕，都不需限制顾客源和系统容量。也就是说，各系统的可能状态集S={0, 1, 2, ……}。按先到先服务(First Come First Service, FCFS)策略画出各系统状态流如图2所示。

图2 公厕排队系统状态流图

2 系统主要性能指标

下面先重点研究最简单的女厕排队系统的主要性能指标。

平均排队等待顾客

平均忙着服务设施F=ρ。

平均队长(即平均排队等待顾客数CW与正在服务顾客数F之和)。

由Little公式[13]，可得顾客在系统中的平均等待时间TW和平均逗留时间(平均等待时间TW与平均服务时间之和)TS。

表1 女厕、男厕和无性别公厕排队系统的性能指标

由表1可得传统公厕排队模型的主要指标如下。

空闲概率即男厕和女厕都空闲概率

PT0=PF0·PM0=

满员概率即男女两厕都满员概率

PTn=PFn·PMn=

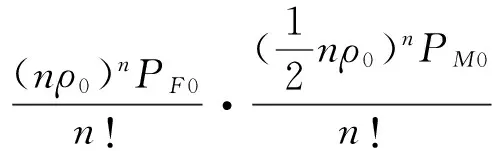
平均等待顾客数即男女两厕平均排队等待顾客数的算术平均值

平均忙着的服务设施即男女两厕平均忙着的服务设施之和

FT=FF+FM=ρ+0.9ρ=1.5ρ。

平均队长即男女两厕平均队长的算术平均值

平均等待时间即男厕和女厕平均等待时间的算术平均值

平均逗留时间即男厕和女厕平均等待时间的算术平均值

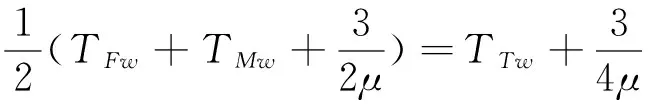
刚到的顾客必须等待概率即刚到男厕和女厕的顾客必须等待概率之和

PTw=PFw+PMw。

3 系统性能仿真

为比较无性别公厕与传统公厕的性能，我们对其进行仿真。女顾客如厕的平均时间为100s[15]，即女厕每个设施的平均服务μ率为0.6人/min。当n=5，λ=2.5人/min时，ρ0=0.833<1，上述各排队系统均会达到平衡状态。此时各排队系统的性能指标如表2所示。

表2 n=5，λ=2.5人/min时各公厕排队系统的性能指标

从表2可以看出，除平均队长外无性别公厕的其他性能指标都优于传统公厕。

μ和n不变且系统能达到平稳状态时，变化对传统公厕和无性别公厕系统性能的影响，如图3所示。

由图3(a)可以看出，无论怎么变化传统公厕的2n个服务设施的空闲概率P0都比无性别公厕大；随的增加，每个排队系统中所有服务设施的空闲概率呈递减趋势。由图3(b)可以看出，因受男厕的影响随的增加传统公厕中两公厕同时满员的概率越来越小于无性别公厕；女厕的满员概率随的增加而呈现先增后减趋势，从而导致传统公厕的满员概率也呈现先增后减趋势。由图3(c)可以看出，因受女厕平均等待顾客随增加而逐渐增加的影

图3 对不同公厕排队系统性能的影响

响传统公厕的平均等待顾客也随增加而呈逐渐增加趋势，而无性别公厕的平均等待顾客随增加而呈微妙增加趋势。由图3(d)可以看出，随增加每个排队系统中平均忙着的服务设施呈线性增加。由图3(e)可以看出，因受平均等待顾客影响传统公厕的平均队长也随增加而呈急剧增加趋势，而无性别公厕的平均队长因受正在服务平均顾客数即平均忙着的服务设施的影响而呈现线性增加趋势，而且当时传统公厕的平均队长超过无性别公厕。由图3(f)、 (g)和(h)可以看出， 随增加女厕和传统公厕的平均等待时间、平均逗留时间和必须等待概率呈急剧增加趋势，而男厕和无性别公厕的平均等待时间、平均逗留时间和必须等待概率呈微妙增加趋势。总之，随增加无性别公厕排队系统的平均队长、平均等待时间、平均忙着的服务设施等各项性能都优于传统公厕。也就是说，无性别公厕不但可以减少排队长度和等待时间，还可以提高系统资源的利用率。

4 结束语

针对公厕排队问题，本文提出了基于M/M/s排队系统的男女分离的传统公厕和无性别公厕排队模型。通过其状态流程图分析和研究系统达到平稳状态时的性能指标如空闲概率P0、满员概率Pn/P2n、平均等待顾客数Cw、平均队长L、平均服务设施数F、平均等待时间Tw、平均逗留时间Ts和刚到顾客必须等待概率Pw等。同时，对各系统进行性能仿真，重点分析和比较传统公厕和无性别公厕排队模型的性能。从研究结果看，无性别公厕无论从服务设施的利用率、顾客的等待时间，还是其他方面都具有比传统公厕更高的性能，从而为解决公厕排队问题提供了一种可行思路和理论依据。

[1] 柏文学. 喜看“公厕标准”进两会议题[J].标准生活, 2012(3)：10.

[2] 马康丁．公厕设计的无障碍与人性化[J]．北京规划建设，2007(6)：35-36．

[3] 夏苏湘，刘 峰，张明成，等．大型展会公共厕所厕位数需求计算方法及参数研究[J]．环境卫生工程，2008，16(1)：41-44．

[4] 管羚雅，林懿琼，谢 盼．浅析武汉公共厕所存在的问题[J]．商场现代化，2012，8(24)：202-203．

[5] 邹 茜，廖 利，吴 丽，等．深圳市公厕规划建设研究[J]．城市管理与科技，2006，8(6)：263-266．

[6] 石之光. 现代城市设计中不可缺少的乐章——公厕的建设[J]．中外建筑，1997(4)：32-33．

[7] Erlang A K. The theory of probabilities and telephone conversations[J]. Nyt Tidsskrift for Matematik B, 1909, 20: 33-39.

[8] Anokye M, Abdul-Aziz A R, Annin K, et al. Application of queuing theory to vehicular traffic at signalized intersection in Kumasi-Ashanti region,Ghana[J]. American International Journal of Contemporary Research, 2013, 3(7): 23-29.

[9] Liu L M, Liu X M, Yao D D. Analysis and optimization of a multistage inventory-queue system[J]. Management Science, 2004, 50(3): 365-380.

[10]Khazaei H, Misic J, Misic V B. A Fine-Grained performance model of cloud computing centers[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24(11): 2138-2147.

[11]Murugesan R, Elango C, Kannan S. Resource allocation in cloud computing with M/G/s-queueing system[J]. International Journal of Advanced Research in Computer Science and Software Engineering, 2014, 4(9): 443-447.

[12]Leonard K. Queueing Systems. Volume 1：Theory[M]. New York: John Wiley & Sons, 1975:102.

[13]陆传赉.排队论[M].2版.北京：北京邮电大学出版社，2009：7-8.

[14]吴 斌.风景名胜区公共厕所设计与研究[D].南昌：南昌大学建筑工程学院，2007.

On the performance of public toilet based on M/M/nqueueing system

WANG Xian-chao1, SHENG Le-yuan1, DONG Shu-yi2,CHENG Hong-mei1, YU Qin1

(1.SchoolofMathematicsandStatistics,FuyangNormalUniversity,FuyangAnhui236037,China；2.No.31MiddleSchool,BengbuAnhui233000,China)

This paper built a public toilet queueing model based on the M/M/n queuing system. The performance of traditional public toilet and asexual public toilet by simulating the queueing model was analyzed. The results illustrated that every performance indicator of the latter was better than that of the former, which could provide an idea and theoretical basis for solving the queue problem.

queueing theory; asexual public toilet; M/M/nqueueing system

2014-04-04

安徽省教育厅高校自然科学研究重点项目(KJ2015A191)；国家特色专业(TS1496)；安徽省质量工程项目(AH201410371084，2013zy167)；阜阳师范学院质量工程项目(2013ZYSD05，2014JXTD01)资助。

王先超(1973-)，男，博士，副教授，研究方向：光计算、数学建模。

O226

A

1004-4329(2015)03-016-05

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)03-016-05