最优控制方法在直线倒立摆中的应用

刘惠超，孔庆忠

(内蒙古工业大学 机械学院，内蒙古 呼和浩特 010051)

最优控制方法在直线倒立摆中的应用

刘惠超，孔庆忠

(内蒙古工业大学 机械学院，内蒙古 呼和浩特 010051)

假设忽略掉倒立摆系统本身不稳定因素(摩擦阻力)的影响后，倒立摆系统就可以看成是一个典型的运动刚体系统。基于牛顿力学定律的数学建模方法，应用二次型最优控制理论对一级倒立摆实现控制，使用在惯性坐标系内的经典力学理论动力学方程，能满足控制系统的一般稳定性和鲁棒性的性能要求。采用MATLAB对倒立摆系统进行仿真模拟实验，并对仿真结果进行分析。

最优控制理论； 倒立摆系统；仿真

0 引言

倒立摆系统是一个快速、多变以及非线性的不稳定系统，但在航天火箭飞行器以及双足机器人行走范围内有着重要的应用。基于我国航天工业的迅速发展，倒立摆的实际研究显得具有重要的应用价值[1]。

1 直线一级倒立摆的数学建模和可行性计算

直线一级倒立摆主要由小车、摆杆等主要部件组成，它们之间自由连接。建立直线一级倒立摆的前提是：1) 小车能够在导轨上自由移动(不考虑摩擦等因素)；2) 铅垂的摆杆可以在竖直的平面内自由地摆动(不考虑系统本身的摩擦等阻力影响)[2]。

一级倒立摆的系统结构简图如图1所示。假定逆时针方向的转角和力矩方向均为正。设M为摆杆的质量；m为小车的质量；Ll为摆杆的长度；O为旋转点坐标；D为摆杆质心坐标；l为点O到点G的距离；J为摆杆的转动惯量；f为小车与导轨间的摩擦系数；T为摆杆绕转动轴的摩擦阻力矩系数；φ为摆杆与垂直向上方向的夹角；F为外界作用力；x为小车运动距离原点的位移；则摆杆和小车的受力情况，如图2。

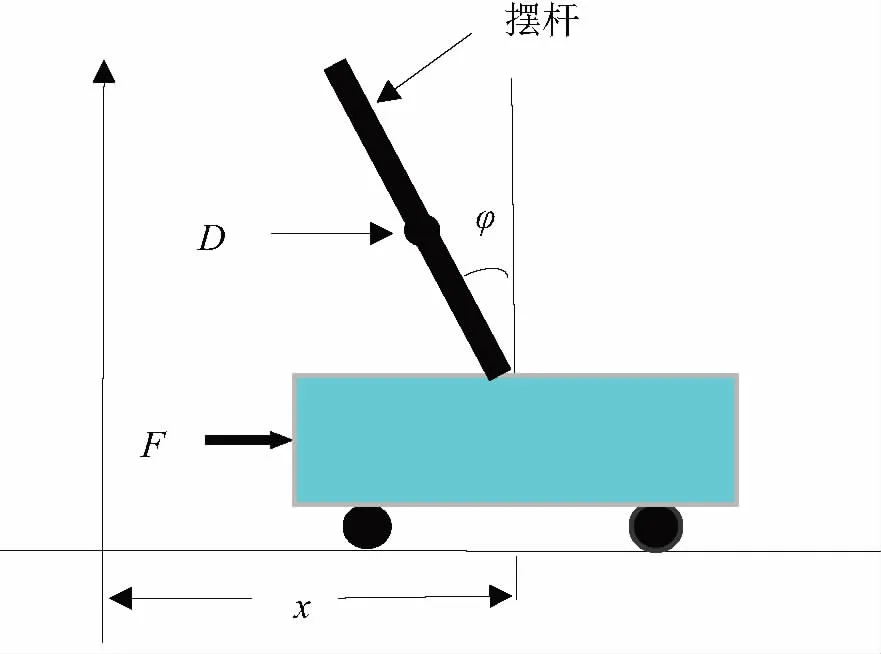
图1 一级倒立摆的结构图

图2 摆杆的受力分析图

1.1 对摆杆进行数学建模，首先对摆杆运动学分析

由图2分析摆杆受力情况，摆杆水平方向受力：

(1)

则摆杆绕O点的力矩平衡方程为：

(2)

1.2 对小车进行数学建模，小车运动学分析如下

小车在水平方向上受力为:

F-f-(Mx'-Ml’sinφ+Mlcosφ)=mx″

(3)

假设令T=m+M，V=J+Ml2，U=Ml

得到了描述一级倒立摆运动的微分方程组：

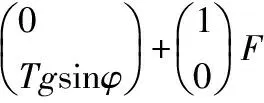
(4)

将矩阵方程式(4)进行理想化处理得到一级倒立摆的微分方程：

(5)

倒立摆实物控制系统中，系统的输出是摆杆的角度，受到控制的是小车的位置，以调整小车的位置来矫正摆杆的角度，所以在进行数学建模时，以角度为受控对象。以摆杆角度为输出时，传递函数为：

(6)

将微分方程式(4)进行线性变化可以得到系统的状态方程：

(7)

假设x″=a,以a做控制输入，状态方程为：

(9)

2 线性二次最优控制的基本原理分析

2.1 线性二次最优控制的主要问题

线性最优控制研究的主要问题是：根据已建立的一个被控对象的数学模型，选择一个在应用范围内可以控制的规律，使得被控对象可以按照事先预定的要求进行控制，并可以使其在某一性能指标到达最优值。

经典的变分理论只能解决控制无约束的问题，但是工程实践中遇到的多为有约束控制。因此，这种线性最优控制的出现可以使工程的应用范围更加广泛，以此成为现代控制理论中核心的成果之一。线性二次型问题可以通过状态反馈实现闭环控制，这个应用在工程上具有重要意义。

2.2 线性最优控制的目标

最优控制的目标是使J→min，其实质是用不大的控制量来保持相对较小的误差，从而使结果达到能量和误差最优的结果。

2.3LQR控制参数的调节

在一般情况下，控制量的权重R增加时，则控制力增加，相应的倒立摆摆杆的角度变化减小，进而速度相对减慢。性能指标函数对于状态量的权重Q中，如果此对角矩阵越大，意味着变量在性能函数中越重要，状态要求的约束越高，其对应的状态参量的响应速度便增加，但是其他变量响应速度相对减慢，

3 直线倒立摆系统在MATLAB程序下进行LQR仿真

直线倒立摆的平面控制流程图，如图3所示。

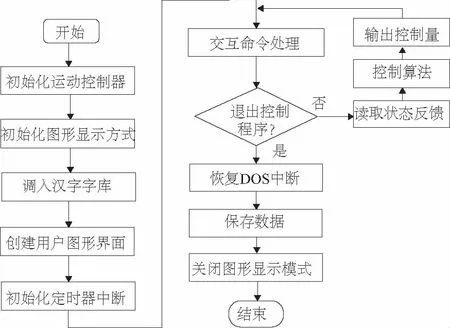
图3 直线倒立摆的平面控制流程图

用MATLAB 7.0对直线倒立摆进行仿真研究，在“Simulink”中构建最优控制模型，模型如图4所示[3]。

图4 Simulink下一级倒立摆的最优控制模型图

单击LQR Controller模块，计算出不同的反馈增益K值，在反馈增益K中包含参量K1、K2、K3、K4，将不同的反馈增益值输入到系统中，得到一级倒立摆的不同的仿真曲线。当按照文中介绍的直线倒立摆的实物参数(小车的质量m=0.618kg,摆杆的长度L=0.350m,摆杆的质量M=0.0737kg，摆杆质心到转轴的距离l=0.1225m)时，得到直线倒立摆理想的仿真曲线，如图5所示。

图5 直线倒立摆理想的仿真曲线

此时，可以从图5中很明显的得出，系统在300μs左右的时间时，达到稳定。随着时间的推移，偶尔出现不稳定的因素，归结为带动小车的轨道的某处摩擦较大。

综上所示，不同的K值影响系统不同的行为，知道K值的计算式根据在最优控制(LQR)下，通过对两个矩阵的数学求解得到的，所以，更改不同的值，得到不同的仿真曲线。改变不同的K值，会得到不同的仿真曲线，但是大致的仿真图像与结论类似，不再一一叙述。

图6 理想的直线倒立摆的仿真参数

4 结论

随着自动控制理论的逐步发展，新的控制方法不断出现，LQR控制方法就是通过对系统线性化处理之后的一种控制方法，具有很好的仿真实验结果。对于具有不稳定性、高阶次、多变量、强耦合的直线倒立摆系统，通过牛顿力学方法和最优控制方法对直线倒立摆进行MATLAB仿真，能更好的显示出LQR控制器的鲁棒性与动态特性[4]。

[1] 张宁. 直线倒立摆起摆与稳摆控制的优化与改进[D]. 大连：大连理工大学，2010:59-60.

[2] 罗晶, 陈平. 一阶倒立摆的PID 控制[J]. 实验室研究与探索，2005, 24 (11):26-28.

[3] 刘金琨. 先进PID控制及其MATLAB仿真[M]. 北京: 电子工业出版社，2003.

[4] 朱文凯. 倒立摆的 PID 与LQR 控制算法的对比研究[J]. 广东自动化与信息工程，2006, 2 (1):1-3.

Application of Optimal Control Method in Linear Inverted Pendulum

LIU Huizhao, KONG Qingzhong

(College of Mechanical Engineering,Inner Mongolia University of Technology,Huhhot 010051,China)

Assuming that the inverted pendulum system itself instability (including the friction force) is ignored, this system can be regarded as a typical motion of rigid body system. Based on the mathematical modelling method with Newton's laws of mechanics, the quadratic optimal control theory is used in primary inverted pendulum control and the inertial coordinate system dynamics equation with the classical mechanics theory is used to be satisfied with the performance requirements of the general stability and robustness of the control system. This article uses MATLAB to simulate the inverted pendulum system and analyzes the simulation results.

optimal control theory; inverted pendulum; simulation

刘惠超(1989-)，女，山东泰安人，硕士研究生，研究方向：智能机器人。

TP273

B

1671-5276(2015)05-0189-03

2014-02-24