基于直接支持向量机的蒸发波导参数反演研究

吕雍正，芮国胜，田文飚

(海军航空工程学院，山东烟台 264001)

大气波导是电磁波在大气传播中的一种异常现象，电磁波会改变原来的传播路径，被陷获在一定高度和范围内的大气波导层中以很小的损耗进行超视距传播，进而影响到雷达和通信系统的使用。随着我国海洋事业的发展，对海洋大气信息的全面掌握尤为紧迫。大气波导影响无线电设备的使用，获得实时大气波导信息对于舰船通信导航、雷达侦察探测和武器精确制导具有重要军事意义。

对海洋大气波导的反演研究由来已久，Krolik［1］最早提出利用雷达海杂波进行大气波导的反演研究，后期的反演研究多由此展开;Yardim 等［2］利用马尔科夫蒙特卡洛方法反演大气折射率;Caglar Yardim 等［3，4］分别采用遗传算法和马尔科夫蒙特卡洛混合算法、卡尔曼滤波和粒子滤波方法估计了波导大气折射率;这些方法对于大气折射率剖面的反演研究都提供了一定思路，但对多参数反演仍存在稳定性差、精度不高和收敛速度慢等问题。

传统支持向量机(SVM)针对有限样本，能够克服局部寻优、泛化能力差和多维数问题，Douvenot［5］采用SVM 进行了波导参数的反演，但存在训练速度慢、算法复杂以及检测阶段运算量大等缺点;杨超［6］提出利用最小二乘支持向量机(LSSVM)反演蒸发波导，LSSVM 把最小二乘法引入到SVM中，简化了计算复杂性，一定程度上提高了反演效率，线性方程组的系数矩阵对称但不正定，影响一些快速算法的使用;本文采用直接支持向量机算法(DSVM)，将超平面的阈值平方项加入到非线性最小二乘支持向量机的目标函数中，求解算法更简单，训练速度快，泛化能力也没有明显减弱。

1 蒸发波导模型选择

蒸发波导建模过程就是构建合适的折射率剖面模型。蒸发波导模型选取的准确与否关系到能否精确有效地反映真实的电波传播环境。环境模型中描述折射率剖面的参数越多，即反演参数向量的维数越高，反演的剖面与实际大气折射率剖面就越接近。实际传播中折射率剖面随距离而变化，但通常认为在水平方向上的变化是缓慢的，因此可以假定在水平距离的某特定间隔内其剖面是不变的。

在电磁波的大气传播中，大气折射率可以由大气温度、相对湿度和压强3 个影响参数表示

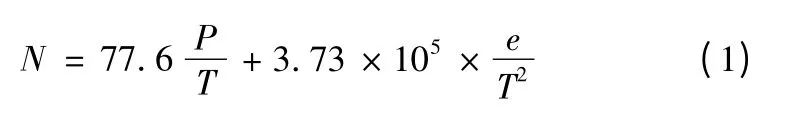
其中:P 是大气压强(hPa);T 是大气温度(K);e 是水汽分压(hPa)。

在实际计算分析中，通常将地球曲面近似为平面处理，用修正折射率M 来表示

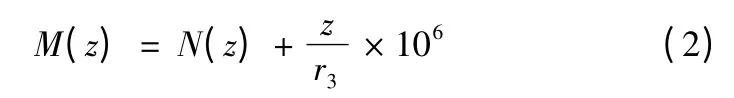
其中:z 表示距离地表的高度(m);re表示地球半径(m)，为常数。

当修正折射率M 和折射率N 满足如式(3)条件下会出现大气波导现象

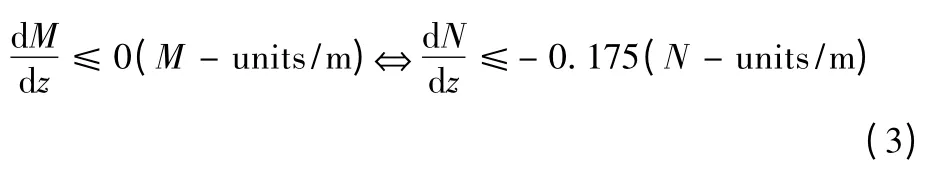
大气波导现象通常分为以下几类:蒸发波导、表面波导、抬升波导以及由3 种波导相互作用形成的混合波导。实验统计，在近海面大气层中，尤以蒸发波导出现的概率最大，通常发生在海面40 m 以下，如我国的南海和东海海域其发生概率高达80%以上。据此，本文主要研究蒸发波导，从美国海军物理实验室提出的五参数经验模型［7］中选取双参数模型［8］作为蒸发波导的模型，能够克服单参数模型下波导高度与强度不一一对应的情况。模型表示如图1 所示。

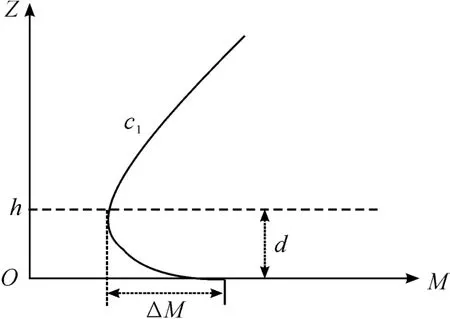
图1 双参数蒸发波导模型

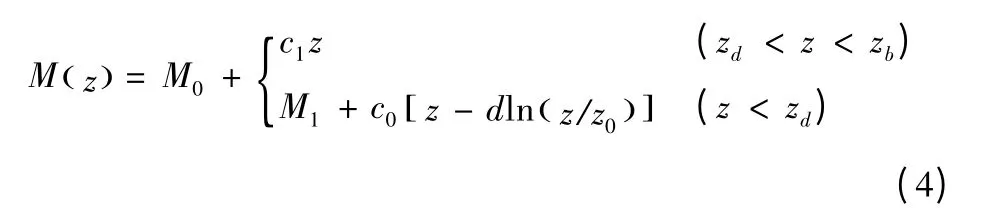
式(4)中:M0为底层修正折射率指数，一般取330 units/m;c0为中性层结折射率剖面有关的经验值，取0.13;c1为波导底层斜率，取值区间为［-1，0. 4］;z0为粗糙因子，取1. 5 ×10-4;zb为蒸发波导顶层高度，取值范围为［0，500］，单位m;d 为蒸发波导高度，当d=0 m 时，对应的是标准大气情况下的折射率剖面

M1=c0dln (zd/z0)+zd(c1-c0)。一旦确定了波导顶层高度zb，就剩下了d 和c12 个参数。

2 蒸发波导传播的抛物方程模型

抛物方程是在求解波动方程时得到的一种近似形式，相比于射线追踪和波导模理论，抛物方程方法对远距离的电磁波传播可以提供更加可靠、稳定的计算。

在直角坐标系中，二维标量波动方程在折射率为n(x，z )的各向同性介质中的场量ψ 满足下面的亥姆霍兹方程［9］

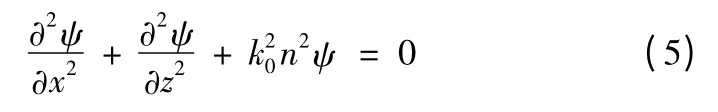
式中:k0=w/c 是真空中的波数;n=n (x，z)是介质的折射指数;x 和z 分别表示地表面的水平距离和距离地表的高度。引入x 轴向衰减函数u (x，z) =ψ(x，z) e-ik0x，得到关于u 的标量方程

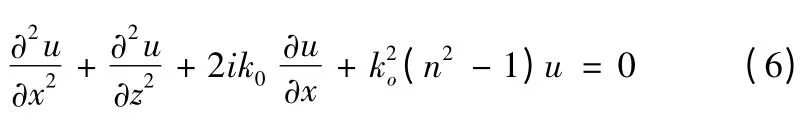
通常传播仰角很小，只考虑前向传播的电磁波，因此所对应的抛物方程的解

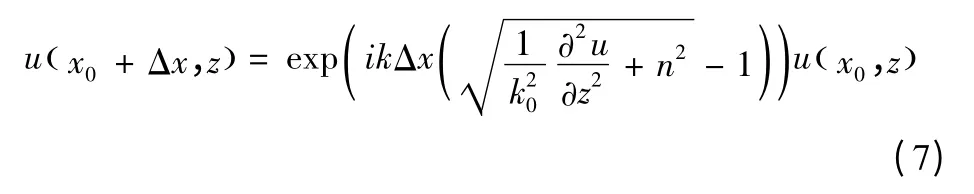
式(7)的求解是一个步进的过程。只要给定一个初始值u (x0，z)，就可以递推得到其他的区域 (x0+Δx，z )内的场分布。

在一定大气波导环境下，接收到的杂波功率可以用雷达方程计算得到

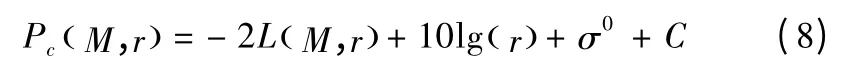
其中:L 为传播损耗，是大气波导参数M 与雷达到海面的距离r 的函数，L 可以由抛物方程来求解，表达式为L = Lf-20lgF，F 为传播因子，Lf为自由空间传播损耗;σ0是海面散射系数，处理时假设它是区域独立性的，当成常数;C 为与雷达发射功率、天线增益等系统参数有关的常数。

3 直接支持向量机

支持向量机(support vector machine)是由统计学习理论发展而来。它以结构风险最小化原则和VC 维(vapnik chervonenkis dimension)理论为基础，取代传统学习算法中的经验风险最小化原则。SVM 基本思想是:通过非线性映像把输入向量映像到高维特征空间，通过引入核函数，从而巧妙地将非线性估计问题转化为高维特征空间的线性估计问题。由于SVM 建立在严格的统计学习理论基础之上，不会陷入局部寻优，有更强的泛化能力，较好地解决了小样本、非线性、高维数和过学习等实际问题。DSVM 问题的求解规划［10］

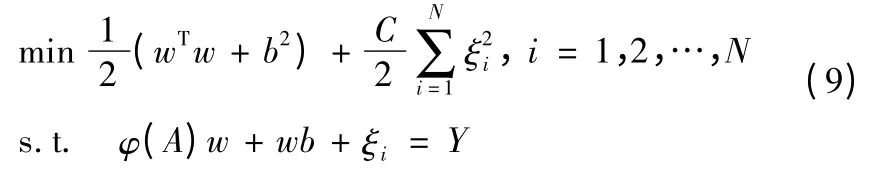
式中:w 为权向量;b 为阈值;ξi∈RN×1为误差向量;C ＞0 为正则化因子。

引入Lagrange 乘子αi，αi∈RN×1，定义其Lagrange 函数为

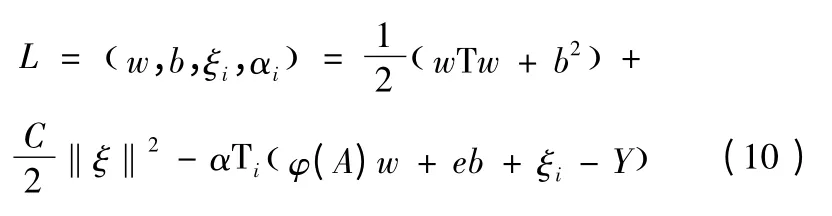
根据KKT(Karush-Kuhn-Tucker)优化条件，对w，b，ξ，α求偏导数并令其为0，可得

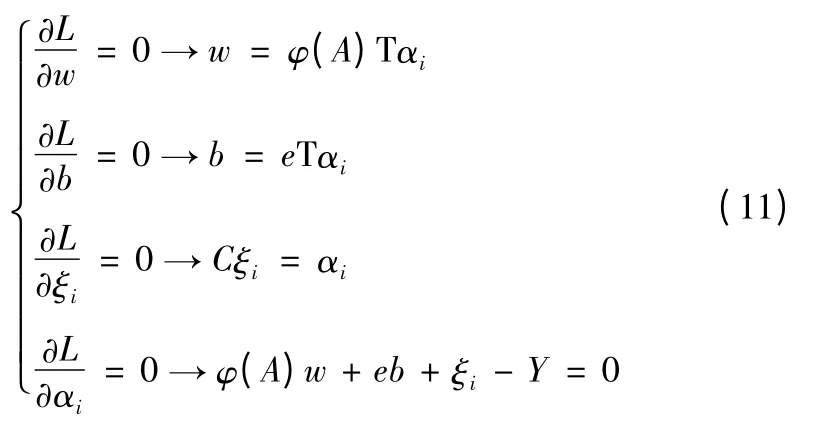
带入消去w、ξi，得到方程

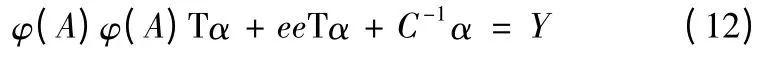
使用核函数K=K (A，A) =φ(A)φ(A)T，有方程

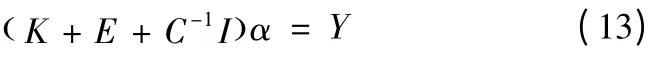
得到回归函数为

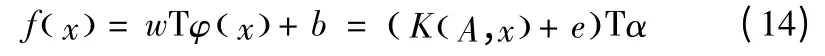
4 仿真分析

蒸发波导的参数反演是复杂的非线性过程，将DSVM 引入到反演蒸发波导的过程中。选取目标函数f 来判别仿真信号功率Pcal与计算得到的信号功率Pobs的符合程度，用于确定构建的波导参数M 与实际波导参数的误差程度。这里选取是Pcal和Pobs的平均值。

4.1 DSVM 对电磁传播损耗的训练分析

给定一组维数为m 的蒸发波导高度z，就可以相应得到m 个M 剖面。利用抛物方程法和雷达方程得到m ×N 的正向功率矩阵。

蒸发波导的高度一般不超过40 m，选取波导顶层高度d=20 m，发射天线高度10 m;电磁波频率区间［1，2］GHz，采样频率0.1 GHz，共11 个采样频率;接收高度区间［10，28］m，采样频率2m，共10 个采样高度;在每个接收高度处检测的传播距离从10 ～60 km 以200 m 为间隔，取251 个点的传播功率损耗作为训练数据，共2 510 个训练样本。输出矩阵对应不同频率和传播距离处的传播损耗组成。并以此输入矩阵和输出矩阵作为训练数据来训练DSVM。

为了验证预测结果的准确性，给出抛物方程(PE)的计算结果与训练模型的传播损耗值的对比图。选取频率为1.5 GHz，接收高度分别为10 m，20 m 时DSVM 的预测损耗值与LSSVM、抛物方程计算值的对比图2、图3。

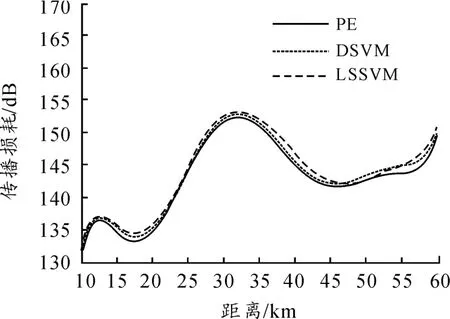
图2 10 m 高度传播损耗

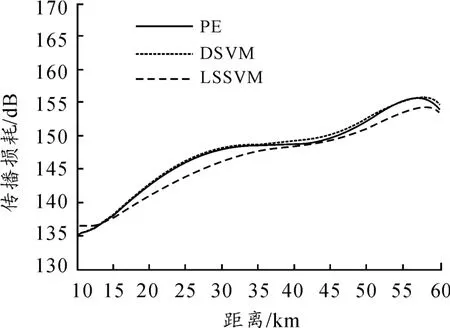
图3 20 m 高度传播损耗

从训练模型的速度上看，LSSVM 用时183 s，DSVM 用时179s，两者所用时间相当，没有明显优势。从对比图中看出，2 种方法的训练结果都与抛物方程给出的传播损耗相近，但DSVM 的训练结果曲线与抛物方程方法计算值吻合结果更精确一些，预测更趋近于抛物方程计算值。据此仿真结果表明对DSVM 在传播损耗的精度训练方面有更好的表现。

4.2 反演折射率剖面准确性验证

折射率剖面与蒸发波导的高度之间的关系式在前面的模型中已经给出，只要反演出高度值和斜率，相应的折射率剖面就可以得到。与前面训练类似，取发射天线高度10 m;对于蒸发波导高度的训练数据，取值区间为［10，40］m，采样频率取3 m，每个高度处对应的接收功率值共11 组训练数据;在每个接收高度处检测的传播距离从10 ～60 km 以200 m 为间隔，取251 个点的传播功率损耗作为训练数据;组成由11 ×251 的输入矩阵，输出矩阵为对应每个波导高度值组成的11 ×1 矩阵。以此输入输出矩阵作为训练数据。

同样的，取蒸发波导高度为18 m，抛物方程计算给出的各对应点处的接收功率值进行反演。由第1 节给出的参数模型作为真实值，对比DSVM 和LSSVM 方法得到的反演折射率剖面图4 可以看出，2 种优化方法给出的反演剖面与真实值接近，训练结果如表1 所示，可以看到，在训练用时方面，DSVM 比LSSVM 要节省1/4 左右，反演得到的蒸发波导高度，DSVM 为19.1 m，LSSVM 为20.3 m，LSSVM 反演结果误差相对较大，DSVM 给出的反演结果更贴近真实值，适用于后续的反演。

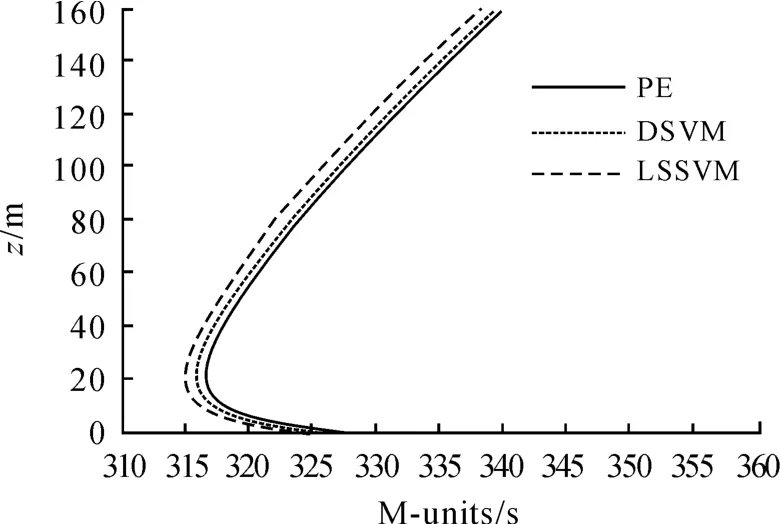
图4 反演折射率剖面对比图

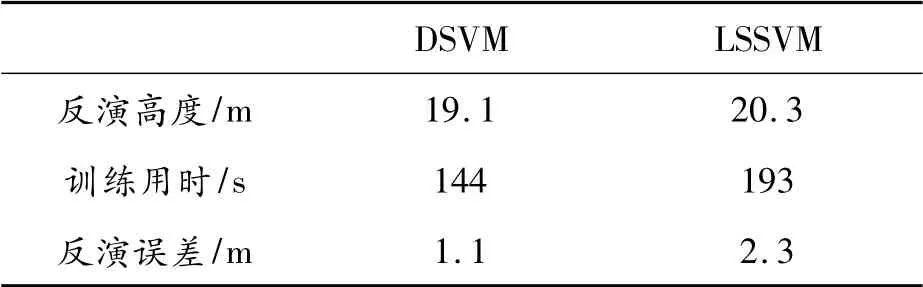
表1 反演用时和误差比较

5 结论

在反演海上蒸发波导的背景下，本文基于直接支持向量机算法进行大气折射率参数的反演。以双参数模型作为本次反演的蒸发波导模型，以抛物方程法计算相应传播损耗，利用改进的算法对大气折射率参数进行优化反演，仿真实验结果表明，新的学习算法在模型的训练速度方面有更为优越的体现，反演结果也更为精确，在蒸发波导反演中有更有效的应用。

［1］Krolik J L，Tabrikian J.Tropospheric refractivity estimation using radar clutter from the sea surface［J］.Proceedings of the 1997 Battlespace Atmospherics Conference，1998:635-642.

［2］Yardim C，Gerstoft P，Hodgkiss W S.Estimation of radio refractivity from radar clutter using Bayesian Monte Carlo analysis［J］. IEEE Transactions on Antennas and Propagation，2006，54(4):1318-1327.

［3］Yardim C，Gerstoft P，Hodgkiss W S.Statistical maritime radar duct estimation using a hybrid genetic algorithms-Markov chain Monte Carlo method［J］.Radio science，2007，42:1-13.

［4］Yardim C，Gerstoft P，Hodgkiss W S. Tracking refractivity from clutter using Kalman and particle filters［J］. IEEE Transactions on Antennas and Propagation，2008，56(4):1058-1070.

［5］Douvenot R，Fabbro V，Gerstoft P，et al. A duct mapping method using least squares support vector machines［J］.Radio science，2008(43):1-12.

［6］杨超，郭立新，吴振森.最小二乘支持向量机在蒸发波导预测中的应用［J］.电波科学学报，2010(8):632-637.

［7］Peter G，Rogers L T，Krolik J L. Inversion for refractivity parameters from radar sea clutter［J］. Radio Sci，38(3):1-18.

［8］王绍班，孙小东，田文飚，等.基于乘子法的海上蒸发波导反演研究［J］. 中国电子科学研究院学报，2013(6):605-610.

［9］M F Levy. Parabolic equation methods for electromagnetic wave propagation［M］.London:IEE Press，2000.

［10］杜喆，刘三阳.最小二乘支持向量机变形算法研究［J］.西安电子科技大学学报，2009(4):331-337.

［11］程焕，谢洪森，孙大军，等.用雷达海杂波反演蒸发波导的蚁群算法［J］.四川兵工学报，2013(1):91-93.