高考导数题的解题方法
安徽省来安县来安中学 李远凯
利用导数研究复杂函数的单调性、极值、最值、参数范围、恒成立(证明)等问题。是解决函数问题的一种重要手段,是衔接初等数学和高等数学的纽带,是高考题中的重点、难点。下面介绍常见的几种导数的解题方法。
一、利用分离变量法解导数中参数范围问题
分离变量法是通过将两个变量构成的不等式(方程)变形到不等号(等号)两端,使两端变量各自相同,解决有关不等式恒成立、不等式存在解和方程有解中参数取值范围的一种方法.两个变量,其中一个范围已知,另一个范围未知。
例1:已知函数

存在单调增区间,求a的范围?

即存在正数解。



记当.
二、利用“特殊值”解导数中复杂问题
“特殊值”在解题中可以缩小参数的范围,有利于参数讨论更加简捷。“特殊值”还可以很快找到函数的关键点,有利于找到更有效的解题方向,达到事半功倍的效果。

k为常数。曲线y=f(x)在点(1 , f (1))处的切线与x轴平行。
(1)求k的值;
(2)求f(x)的单调区间;
(3)设证明:对任意x>0都有.。
解(1)由题意得:

∵f′(1)=0,∴k =1.

∴f (x)在(0,1)上单调递增;在(1,+∞)上单调递减。
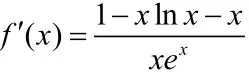


令,令,得。



即对于任意x > 0都有.
注:在第(2)问中,利用特殊值求函数的单调区间就很简捷了。
三、利用“构造函数”解有关导数题
导数中有很多创新题、复杂题、不等式证明等题型,可以通过构造合适的函数就可以迎刃而解。
1.对导函数进行研究构造二次导数
(1)讨论函数 f (x)的单调性;
(2)若在(1,+∞)上恒成立,

令

在(0,+∞)上单调递增。
当,即时,
令

所以 f (x )在(0,x1),(x2,+∞)上单调递增;
在( x1,x2)上单调递减。
(2)转化为:在(1,+∞)上恒成立.
令,

F′(x)在(1,+∞)上单调递增,则
则F(x)在(1,+∞)上单调递增,则.得a≤1,又a>0,所以a∈(0,1].
2.构造适当的函数证明不等式
例4:已知函数,

(1)若不等式在x∈[0,+∞)时恒成立,求实数a的取值范围。
(2)当a=1时,证明:
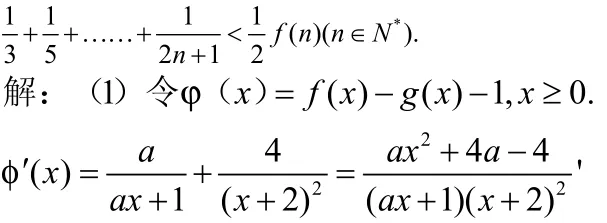
∴当a ≥ 1时,φ(x)在x≥0上单调递增的,成立;
当a ∈ ( 0,1)时,φ(x)在上单调递减的,使得,不符合题意。
∴a≥1.




分析:本题(1)中利用到特殊值减少了解题步骤;(2)中利用函数单调性加以证明不等式,简明方便。
导数作为解决数学问题的一种工具,它为高中数学注入了新的活力。对于一些常见方法的掌握能更加准确快捷的解决导数中的复杂问题。关于难繁的导数大题,解题的方法可以用这样的顺口溜去记忆:关注函数定义域,求导公式要牢记。求参范围用分离,若遇繁难找亲戚(特殊值)。构造函数再分析,如若困难返回去。分类讨论顶上去,细心认真放第一。无能为力把家分(分拆多个简单函数),化繁为简解难题。

