非协调网格在结构动力分析中的应用

耿长春，汪基伟

(1.中交第四航务工程勘察设计院有限公司,广东广州 510000; 2.河海大学,江苏南京 210000)

非协调网格在结构动力分析中的应用

耿长春1，汪基伟2

(1.中交第四航务工程勘察设计院有限公司,广东广州 510000; 2.河海大学,江苏南京 210000)

水利工程中的结构往往体形巨大且复杂，采用非协调网格技术可以减少结点数量，降低网格剖分难度。文章采用形函数插值法推导了非协调网格过渡单元的动力平衡方程，给出了非协调网格过渡单元的刚度矩阵、质量矩阵的计算公式。对某一出水池建立了一致网格和非协调网格两种模型，用自编程序对两种模型进行了动力分析。通过对比分析两种模型的计算结果，证实非协调网格技术应用于此类结构是可行的，高效的。

有限元； 非协调网格； 自振特性； 动力响应； 刚度矩阵； 质量矩阵

1 非协调网格的应用

建立合理的有限元模型是混凝土结构有限元分析的首要任务。在建立有限元模型时常会遇到下列问题：(1)水工结构(如坝、水闸等)有限元计算时，通常取地基在各个方向上的尺寸为建筑物高度的一倍以上。若采用一致网格，地基在水平方向的网格与上部结构相同，这样有可能使地基的单元数超过上部结构。由于模型总结点数受到计算机性能的限制，对于大型结构，不得不采用较粗的网格而降低计算精度。(2)对于体型比较复杂的结构，采用一致网格剖分会有困难，如水电站蜗壳中的导叶与坐环。

采用非协调网格技术可以在一定程度上解决上述问题。所谓非协调网格技术就是对结构进行网格剖分时采用了多于一种的网格尺度的单元。在不协调网格界面上，以网格尺度较大单元所包含的界面上的结点作为基本结点，而界面上与网格尺度较小单元相应的结点作为从结点，建立从结点与基本结点的线性插值关系，从而导出以基本结点位移作为求解变量的非协调网格协调位移解法[1]，这种连接两种网格尺度单元的区域即为过渡单元。如此，可方便网格剖分，节略单元与结点，减小计算规模。

文献[2]～文献[8]采用构造界面过渡单元、最小势能原理等方法来解决非协调截面的协调性，验证了非协调网格应用于结构静力分析的合理性。文献[9]、文献[10]利用非协调网格对二维无限地基和二维重力坝进行了动力特性计算。本文首先根据结点位移协调性推导出三维非协调网格过渡单元的刚度矩阵与质量矩阵公式，并根据公式编制了可应用于实际工程中的三维动力分析程序。

2 非协调网格过渡单元的刚度矩阵与质量矩阵公式推导及程序实现

为推导出非协调网格过渡单元的刚度矩阵与质量矩阵，本文先列出空间8～20结点等参单元的刚度矩阵与质量矩阵计算公式。图1所示为空间8～20结点等参单元，该单元1～8结点为角结点，9～20结点为中间结点，任一个中间结点均可删去。

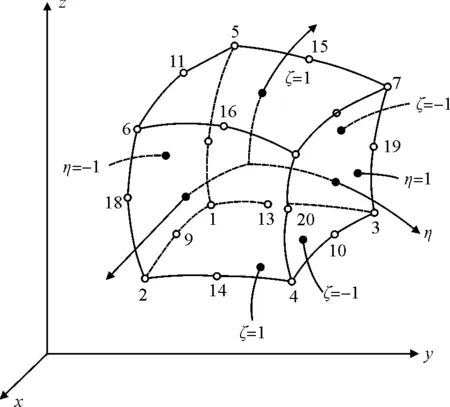
图1 8～20结点空间等参单元

空间8～20结点等参单元的刚度矩阵与单元质量矩阵计算公式为：

(1)

下面以图2所示过渡单元为例，来推导过渡单元的刚度矩阵和质量矩阵。在图2中，块体单元a、p和s均为8结点等参单元，单元a网格尺寸小，称为细单元；单元p和s网格尺寸大，称为粗单元。细单元a的有些结点(最多4个)不与粗单元p和s等单元的结点相连，而是交与粗单元p和s等单元的表面E上，定义这些结点为虚结点(其中虚结点在单元p上时记为p*，在单元s上时记为s*，以此类推)，其余结点为实结点。虚结点的物理量(位移、速度与加速度)不能作为运动方程中的未知量，只能由与其相交的粗单元的结点物理量通过形函数插值得到。为了简单明了地表达公式，下文的公式中只具体写出有关虚结点p*和s*的部分，有关虚结点q*和r*的部分由“…”代替。

图2 非协调网格过渡单元示意

细单元a的结点位移为：

ae=[u1v1w1…up*vp*wp*…us*vs*ws*…wn]

(2)

其中：下标为1～n的变量为细单元上实结点的位移；下标为p*、s*的变量为虚结点的位移。细单元中的虚结点位

移可由与其相交的粗单元结点位移通过形函数插值得到：

(3)

(4)

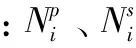
因此细单元结点位移可表示为：

(5)

式(5)可简写成：

ae=Ta′e

(6)

其中：a′e和T分别为：

(7)

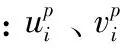
(8)

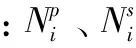
细单元内任一点的位移为：

(9)

式中:N为细单元的形函数矩阵，表达式如式(4)所示。

细单元的应变可表示为：

ε=Bae=BTa′e

(10)

式中:B为应变转换矩阵。

细单元的应力可表示为：

σ=DBae=DBTa′e=[S1S2…Sn]Ta′e

(11)

式中：Si为应力转换矩阵，Si=DBi；D为弹性矩阵。

作用在细单元体积上的作用力为：

(12)

将式(9)代入式(12)，得到：

(13)

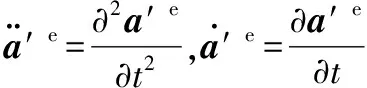
(14)

细单元的等效结点荷载为：

(15)

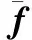
(16)

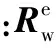
由虚功原理可得平衡方程：

Re=∫veBTDBdvae=∫veBTDBTdva′e

(17)

将式(17)代入式(16)可得：

(18)

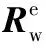
(19)

式中：k′e为细单元刚度矩阵；m′e为细单元质量矩阵；c′e为细单元阻尼矩阵。

(20)

式(20)中的细单元刚度矩阵与细单元质量矩阵的计算公式可转化为：

(21)

比较式(1)和式(21)可知，非协调网格过渡单元的单元刚度矩阵k′e是在一般单元的单元刚度矩阵ke的两边分别乘以转换矩阵TT和T；非协调网格过渡单元的质量矩阵m′e也是在一般单元的单元质量矩阵me的两边分别乘以转换矩阵TT和T。此时得到的单元质量矩阵也是一致质量矩阵。

在等参单元中任一点的坐标可表示为：

(22)

式中：N(ξ,η,ζ)为三维等参单元的形函数矩阵；X，Y，Z为单元结点坐标向量。对式(22)微分可得：

(23)

式中：J为Jacobian矩阵，对整体坐标中的一点P(x,y,z)，其局部坐标(ξ,η,ζ)应符合下式：

(24)

可用牛顿迭代法求解式(24)，迭代格式为：

(25)

(26)

式中：Jn=J(ξn,ηn,ζn)；Nn=N(ξn,ηn,ζn)。

用牛顿-拉斐逊法求解非线性方程组时，在真实解附近具有二阶收敛速度，可较快地将整体坐标转换为其相应的局部坐标。

3 应用实例

本文利用上述过渡单元的公式编制了空间非协调网格动力分析程序，对某一出水池建立了一致网格和非协调网格两种模型，并用自编程序对该结构进行动力计算。一致网格模型如图3所示，整个模型共划分了65 257个结点，52 956个单元。非协调网格模型如图4～图6所示，该模型共划分了41 619个结点，32 320个单元，其中虚结点有1 840个，比一致网格模型节省了36%的结点数目。

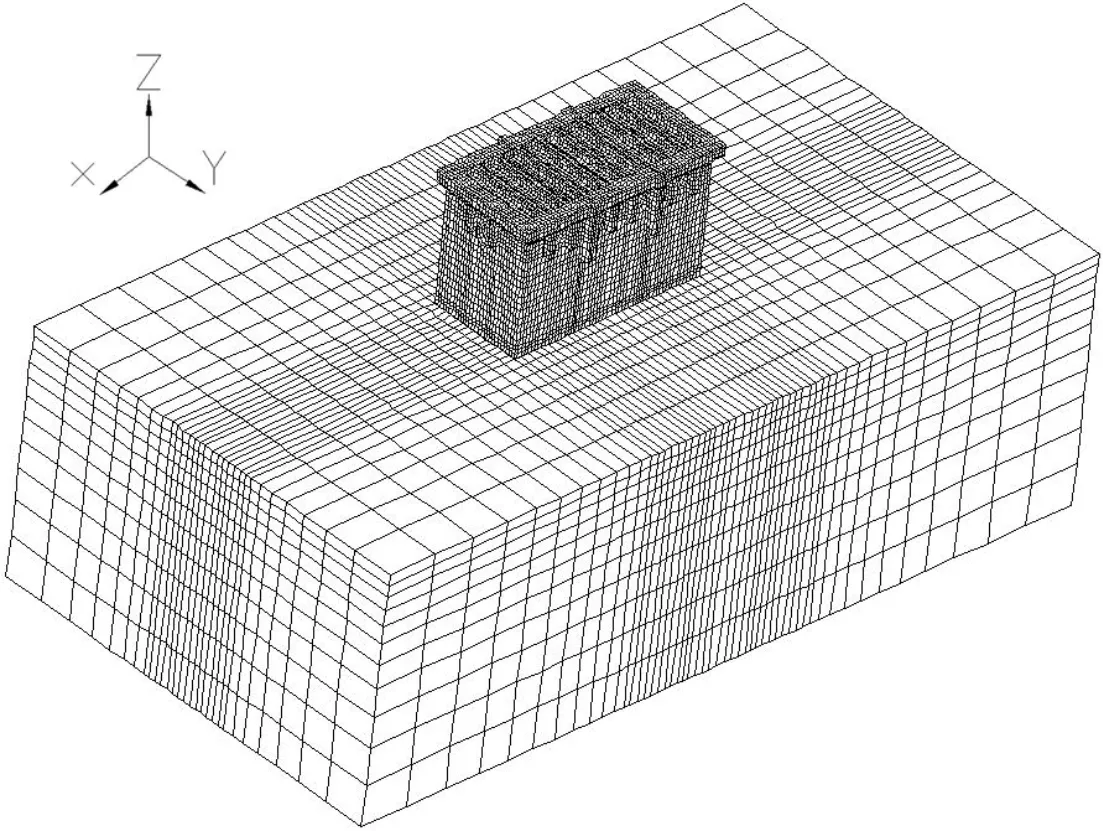
图3 一致网格计算模型

图4 非协调网格计算模型

图5 非协调网格横向剖面示意

图6 非协调网格纵向剖面示意

表1给出了两种模型下结构前九阶自振频率及振型描述。

由表1可以看出，两种有限元模型得到的结构自振频率值非常接近，最大相差5.03%，振型相同，这说明了非协调网格技术应用于求解这类工程自振特性是合理可行的。

本文选用El-centro(1940,NS) 地震波，最大加速度峰值为1.962 m/s2，时间历时20 s，共有1 000个时刻，对两个模型进行了时程分析，一致网格模型费时50 h，而非协调网格模型只用了26 h。在出水池结构上取一个点来分析结构在横向地震波作用下的位移响应。为节约篇幅，图7列出两种模型下该点在Y向和Z向的位移时程曲线。

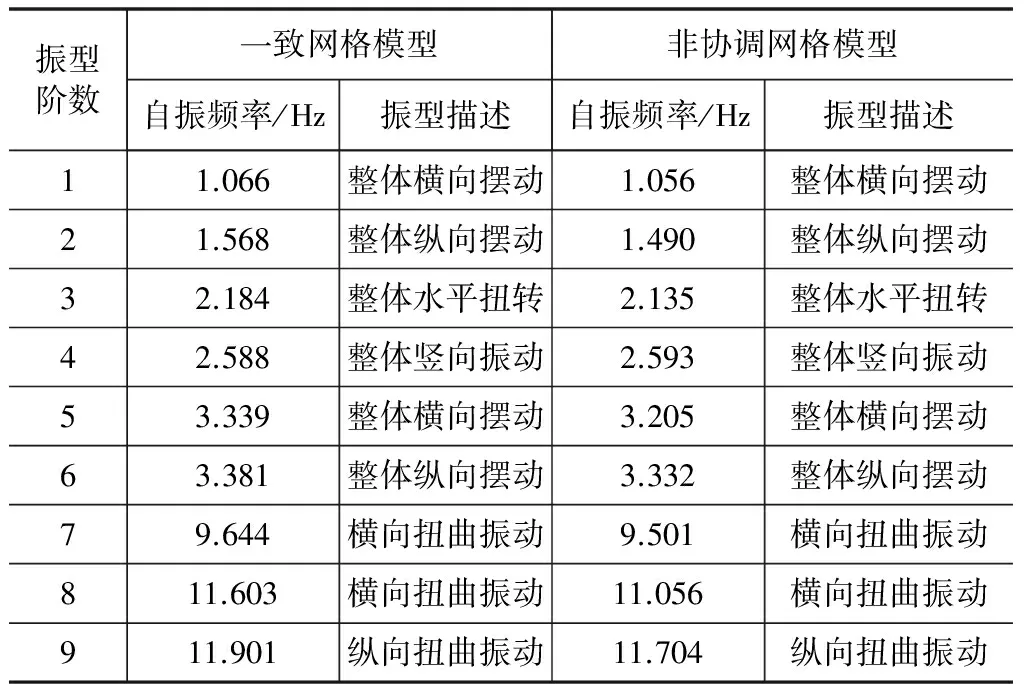
表1 自振频率及振型对比

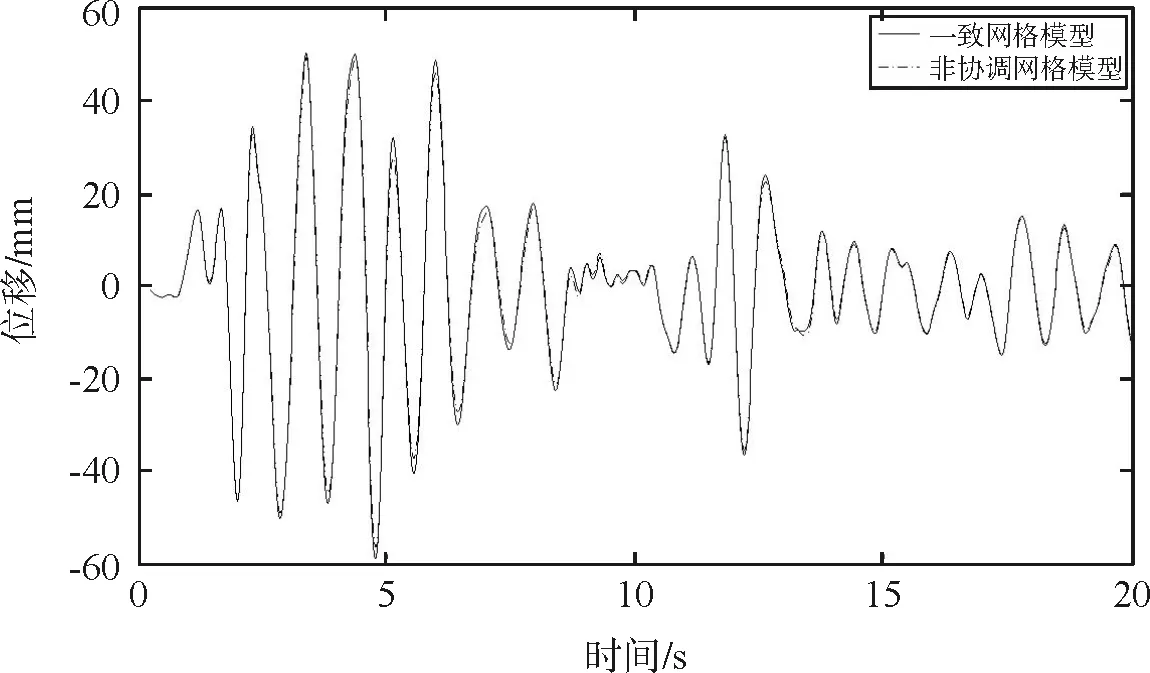
Y向(Y- direction)

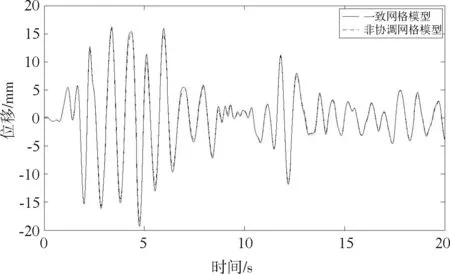
Z向(Z- direction)图7 两种模型下该点的位移时程曲线

由图7可见，两种模型所得的A两点在Y向、Z向的位移的最大误差为6.26 %，其中最大值的误差只有3.70 %，说明非协调网格技术应用于这类工程有足够的精度，满足工程精度要求。

4 结束语

在满足工程精度要求的情况下，在大型工程动力分析中应用非协调网格技术可大为减少结点数目，极大提高计算效率，节省计算时间，该技术可广泛地应用到实际工程中。

[1] 李同春,李淼,温召旺,等.局部非协调网格在高拱坝应力分析中的应用[J].河海大学学报:自然科学版,2003,31(1):42～45

[2] Zienkiew iczO C. The Finite ElementM Ethod[J].Third edition.London:MCGRAM-HLL Book Company Limited,1977,158-160

[3] 王爱民,王勖成.有限元计算中疏密网格间过渡单元的构造[J].清华大学学报:自然科学版,1999,39(8):101-103

[4] 朱以文,徐晗,蔡元奇.交界面非协调网格连结的新约束方程法[J].武汉大学学报:工学版,2003,36(6):47-69

[5] 朱以文,蔡元奇,李伟.等参元逆变换算法在渗流位移耦合场分析中的应用[J].计算力学学报,2002,(2) :233-235

[6] 强天驰,寇晓东,周维垣.三维有限元网格加密界面协调方法及在大坝开裂分析中的应用[J].岩石力学与工程学报,2000,19(5):562-566

[7] 韦未,李同春,牛志伟,等.局部网格加密技术在混凝土裂缝扩展模拟中的应用[J].华南农业大学学报,2007,28(4):112～116

[8] Carpnteria.Valentes, Ferrarag. Experimental and Numerical Fracture Modeling of a Gravitydam[J].BAZANT,ZP.Fracture Mechanics of Concrete Structures. New York: Elsevier, 1992: 351-360

[9] 贺向丽,李同春.基于逐步扩大网格法的饱和无限地基动力分析[J].工程力学,2010,27(4):149-184

[10] 陈礼平,刘国明.非协调网格在重力坝动力特性有限元计算中的应用[J].福州大学学报:自然科学版,2005,33(1):84-88

耿长春(1988～)，男，硕士，助理工程师，主要从事计算方法研究和结构设计；汪基伟(1962～)，男，教授，博士，博导，主要从事钢筋混凝土结构限裂配筋研究和结构静动力分析。

TV313

A

[定稿日期]2014-08-27