沥青混合料蠕变柔量转换为松弛模量的研究

黄文柯，张丽娟，张肖宁，邵申申

（华南理工大学土木与交通学院，广东广州 510640）

沥青混合料的路用性能十分复杂，但其力学行为主要表现为粘弹特性［1］。沥青混合料可以看作一种简单的热流变材料，其粘弹性力学行为的研究已经成为这一领域的主流研究方法。因此，确定沥青混合料的粘弹性参数，是研究沥青混合料粘弹性能的基础。

松弛模量与蠕变柔量是沥青混合料静态粘弹性能的基本方程，是研究沥青混合料粘弹性物理学性能的重要参数。其确定方法［2］有直接拉伸试验、应力松弛试验和蠕变试验等。周志刚［3］从沥青混合料蠕变特性出发，通过直接拉伸试验，确定了沥青混合料粘弹性参数。郑健龙［4］根据应力松弛试验，运用粘弹性力学相关理论，对沥青混合料的粘弹性参数测定方法进行了分析。

应力松弛试验是在试验开始的很短时间内输入一定的应变。然而，直接利用松弛试验测定松弛模量，往往会造成较大的误差，而且操作上也有一定的困难。而利用沥青混合料复数模量，确定松弛模量，已有许多学者研究并取得了一些成果。赵延庆［5］利用沥青混合料复数模量试验结果，确定沥青混合料存储模量主曲线，利用配置法和相关的粘弹性理论关系式，将沥青混合料的存储模量转化为沥青混合料的松弛模量。YAN［6］根据沥青混合料动态扫描数据，运用非线性拟合工具与矩阵的方法，得到相同的广义Maxwell模型的Prony级数表达式的参数。刘孝敏［7］在分析前人成果的基础上，给出了复模量－松弛模量的相互转化关系。然而，在测定沥青混合料的复数模量时，需要在若干个温度下进行试验。而且，在每一个温度下，还需要测定若干个不同角频率沥青混合料的复数模量，才能得到沥青混合料的动态模量和相位角。

沥青混合料单轴蠕变试验较为简单，而且容易实现。本研究拟利用不同荷载水平下沥青混合料蠕变柔量的拟合结果，根据沥青混合料蠕变柔量与松弛模量之间的转换关系，确定松弛强度。以期为沥青混合料粘弹性能进一步分析提供方法。

1 沥青混合料松弛模量和蠕变柔量的Prony级数表达式

沥青混合料是典型的线性粘弹性材料。通常运用线性粘弹力学，研究和分析沥青混合料的性质。线性叠加原理是粘弹性力学中最基本但最重要的原理（也叫Boltzmann叠加原理）之一，最早由Boltzmann作为经验关系提出。线性粘弹性材料单轴、抗老化及等温本构方程为：

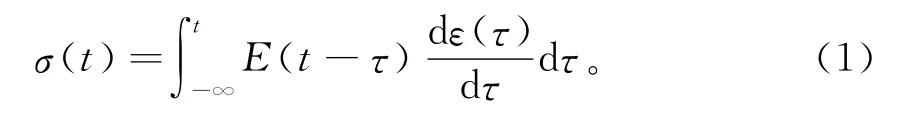
或

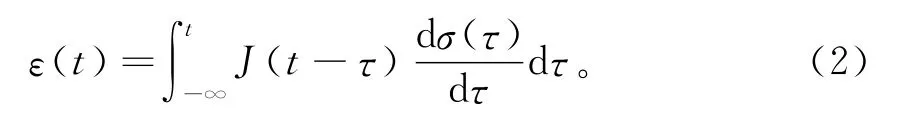
式中：E（t）为松弛模量；J（t）为蠕变柔量；σ为应力；ε为应变；t为时间；τ为积分变量。

描述粘弹性本构关系时，可以用弹簧和粘壶组合的机械模型来解析材料的有关性质。广义Maxwell模型由一个弹簧和m个并联的Maxwell单元组成，如图1所示。

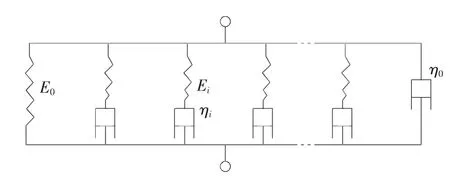
图1 广义Maxwell模型Fig.1 General Maxwell model

模型的松弛模量为：

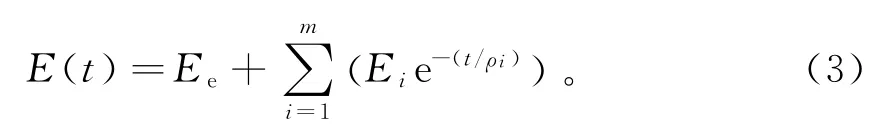
式中：Ee为静弹性模量；Ei为松弛强度；ρi为松弛时间。

蠕变柔量可以通过由一个弹簧、一个粘壶和n个Voigt单元串联而成的广义Kelvin模型表示，其组合方式如图2所示。

模型的蠕变柔量为：

式中：Jg为玻璃态柔量；η0为零剪切粘度；Jj为延迟强度；τj为延迟时间。

式（3），（4）中的系列表达式被称为Prony级数表达式。通过试验，测定了粘弹性参数Ji，τj，Jg，η0，Ee，Ei及ρi，即确定表征沥青混合料粘弹性能的松弛模量和蠕变柔量。该级数表达式表征了恒定荷载作用下沥青混合料的蠕变柔量和松弛模量随时间的变化关系。

2 松弛模量与蠕变柔量之间的转换

粘弹性材料的松弛模量E（t）与蠕变柔量J（t）之间不是简单的倒数关系，它们之间存在一个卷积积分的形式：

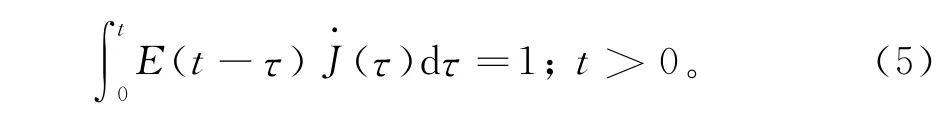
由方程（5）可知，当蠕变柔量J（t）已知时，通过积分，可以确定松弛模量E（t）；相反，当松弛模量E（t）已知时，通过积分，可以确定蠕变柔量J（t）。Park［8］给出的方法为：当松弛模量E（t）已知时，将式（3）和（4）代入式（5），并引入狄拉克δ函数，将式（5）化简为矩阵形式，求解蠕变柔量J（t）。当蠕变柔量J（t）已知时，求解松弛模量E（t）却没有进行推导。本研究利用文献［8］提供的方法，将已知的蠕变柔量J（t）代入式（5）进行推导，并将推导结果用矩阵的形式表示：

或者AkiEi＝Bk；i＝1，2，…，n；k＝1，2，…，p。

式中：tk（k＝1，2，…，p）为与式（5）积分上限相对应的离散时间。

式（4）中的玻璃态柔量Jg可以由Ee＝（Jg＋得到。

3 模型选择及试验

为了验证推导公式的合理性和适用性，本研究将对基质沥青和SBS改性沥青2种胶结料的AC－13C沥青混合料在25℃温度环境下进行不同荷载水平的单轴静载蠕变试验。其中：基质沥青混合料的荷载水平分别为0.5，0.7和1.0MPa，SBS改性沥青混合料的荷载水平分别为1.0，1.2和1.5MPa。本实验试验在MTS810万能材料试验机上进行。

3.1 模型选择

张丽娟［9］利用非线性数学拟合工具，对八单元广义Maxwell模型和广义Kelvin模型进行了参数拟合，发现八单元广义Maxwell模型Prony级数表达式能表征基质、改性沥青混合料的剪切松弛模量随时间的变化关系；在恒定荷载作用下，八单元广义Kelvin模型能表征基质、改性沥青混合料的蠕变柔量随时间的变化关系。本研究中，广义Maxwell模型和广义Kelvin模型都采用八单元（n＝8）Prony级数表达式。对于式（6），当选取的时间点与单元个数相同（即p＝n＝8）时，运用配置法，求解方程；当选取的时间点大于单元个数（p＞n）时，即式（6）的方程个数大于未知数，使用最小二乘法，求解方程。本研究采用2种方法求解方程，并对2种方法的计算结果进行对比。

延迟时间谱和松弛时间谱通常为预先给定的一系列时间点。延迟时间谱取τj＝10j－4，j＝1，2，…，8；松弛时间谱取ρi＝10i－4，i＝1，2，…，8。

3.2 试验原材料

试验用沥青为70＃基质沥青和SBS改性沥青，集料采用花岗岩。级配为AC－13C，各筛孔集料通过百分率见表1。沥青用量为4.8%。

表1 AC－13C沥青混合料矿料级配组成Table 1 Gradation compositions of AC－13Casphalt mixtures

3.3 单轴压缩静载蠕变试验

根据《公路工程沥青及沥青混合料试验规程》（JTG E20－2011）中的有关规定，采用旋转压实试件制作方法，成型直径为100mm、高度为100mm的圆柱体沥青混合料试件。试件脱模后，将试件置于25℃的环境箱中养护12h。为了消除试验机的上、下压板与试件端部的摩擦，在试件上、下端各垫一块聚四氟乙烯薄膜。将试件置于工作台后，先对试件加载进行100N的预压，持续1min，使试件与上、下加载板接触良好。然后，迅速加载到预定的荷载，加载试件为3 600s，每秒采集一个数据点。2种胶结料的AC－13C沥青混合料在不同荷载水平下的蠕变柔量曲线如图3所示。利用式（4），对蠕变柔量数据进行非线性拟合。25℃温度下的沥青混合料可以认为是粘弹性固体，因而Ee＞0，η0→∞。蠕变柔量拟合曲线如图4所示。

图3 蠕变柔量曲线Fig.3 Compliance curves

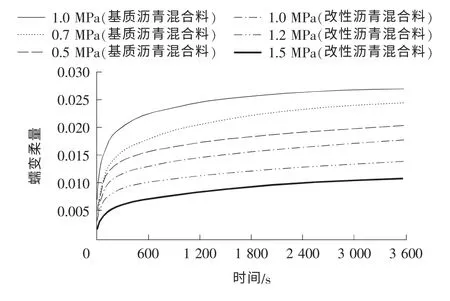
图4 蠕变柔量拟合曲线Fig.4 Nonlinear fitting of compliance curves

从图3，4中可以看出，不同荷载水平下的2种沥青混合料蠕变柔量参数符合沥青混合料的蠕变性质，非线性拟合相关系数在0.998以上。这说明拟合的蠕变柔量方程能预测沥青混合料的蠕变性能。

4 计算及结果分析

根据推导出来的松弛模量与蠕变柔量之间的矩阵转换关系式（6），利用蠕变柔量拟合结果，通过求解沥青混合料松弛模量与蠕变柔量矩阵，得到松弛强度。为了使时间点tk覆盖较宽时间跨度范围，本研究分别采用配置法和最小二乘法2种方法，求解矩阵方程式（6）。tk为预先给定的一系列时间点，而且tk（k＝1，2，…，p）的选择基于求解方法。对于配置法，tk＝1×10k－4（k＝1，2，…，8）；对于最小二乘法，tk＝10（k－1）／2－3（k＝1，2，…，20）。

4.1 配置法求解方程组

配置法是指预先指定配置点，配置点个数与待求未知量个数相同，通过求解方程组，得到所求的未知量。运用配置法，时间点取tk＝1×10k－4（k＝1，2，…，8）并代入式（7），（8），矩阵A变成一个8×8的方阵，矩阵B是一个8×1的矩阵。松弛模量未知参数为8个，实际上是求解含有8个方程的方程组，未知量为8个，未知量与方程数量相等。化简方程组式（6），E＝A－1B，求解出矩阵E，即沥青混合料松弛模量。通过计算，得到松弛强度，其结果见表2。

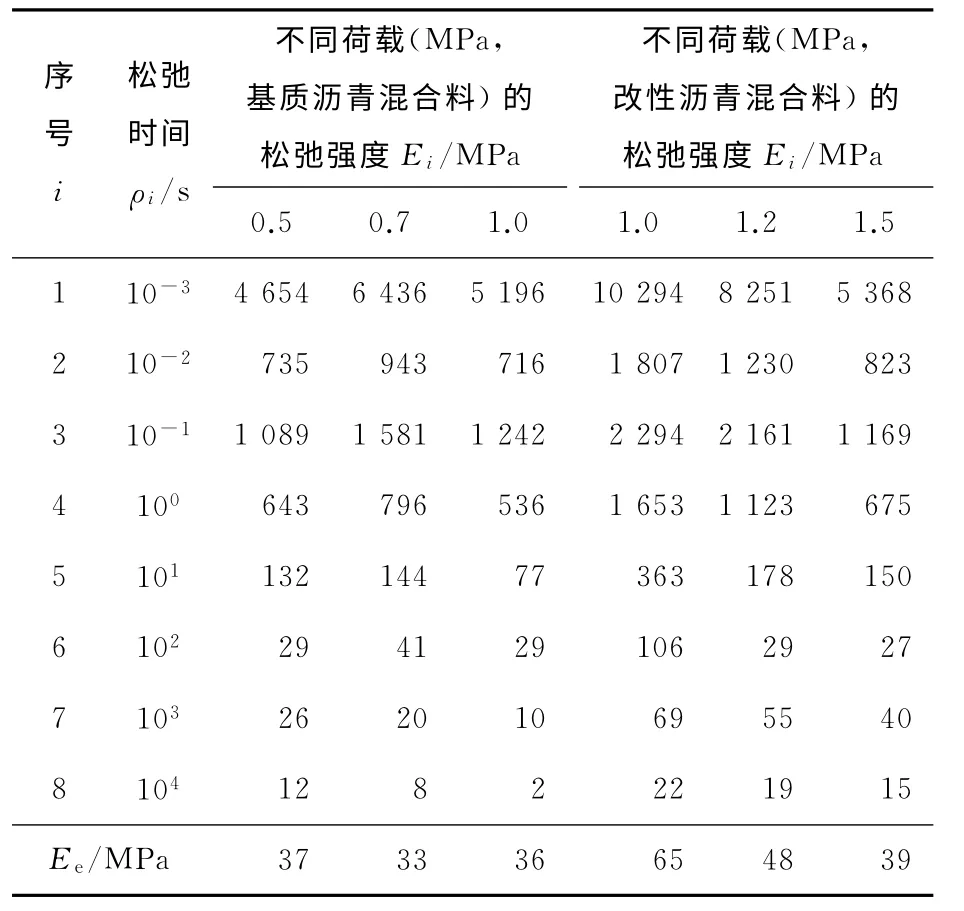
表2 由AC－13C蠕变柔量计算松弛模量结果Table 2 Relaxation modulus results calculated by the AC－13Ccreep compliance

4.2 最小二乘法求解方程组

当选取的时间点大于未知量个数时，利用最小二乘法，求解未知量。时间点取tk＝10（k－1）／2－3（k＝1，2，…，20），同理，代入式（7），（8），矩阵A变成一个20×8的矩阵，矩阵B是一个20×1的矩阵。然而，蠕变柔量未知参数为8个，方程数量为20个，方程数量大于未知量个数，属于线性超定方程组，方程组没有精确解。运用最小二乘法，即min‖AE－B‖2，求出D的最优近似解。可以用ATAE＝ATB求解，但比较低效。常见的解法是对矩阵A进行QR分解，即（A＝QR）。因而，有min‖AE－B‖2＝min‖QRE－B‖2＝min‖REQTB‖2。这个过程可以通过Matlab编程实现。通过将有关参数代入Matlab程序中进行计算，得到松弛强度，其结果见表3。

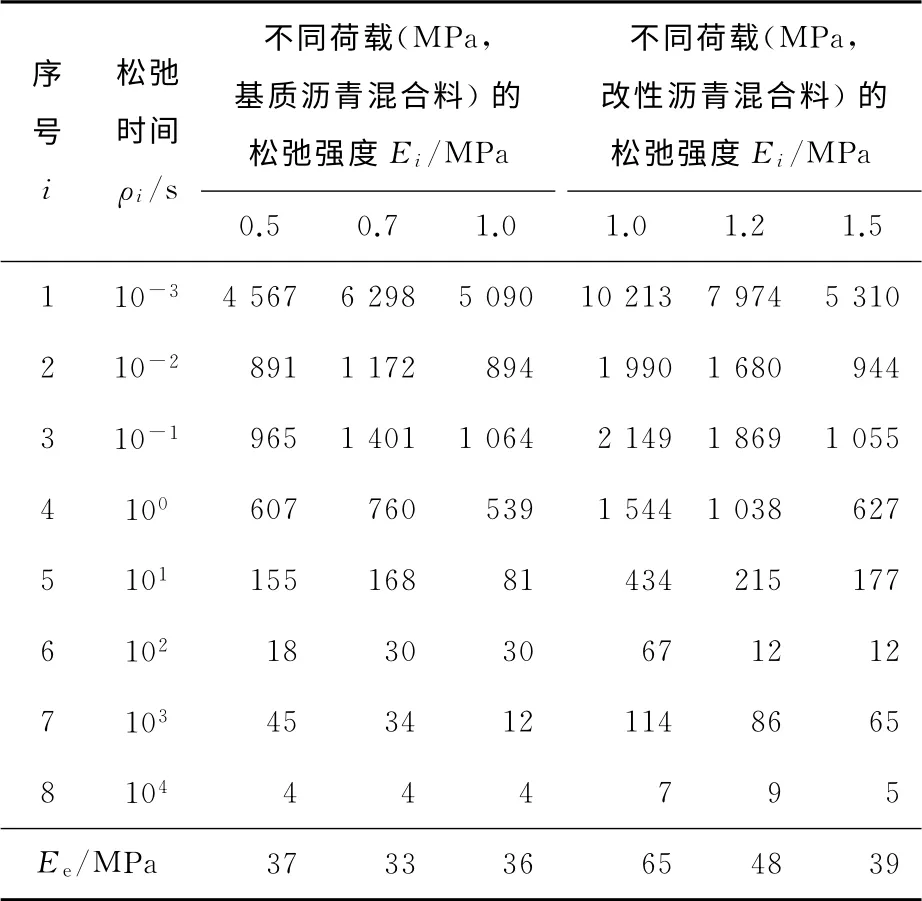
表3 由AC－13C蠕变柔量计算松弛模量结果Table 3 Relaxation modulus results calculated by the AC－13Ccreep compliance

4.3 结果分析

基于配置法和最小二乘法，求解的松弛模量曲线如图5所示。这2种方法计算得到的松弛模量曲线符合沥青混合料松弛性质。这表明：利用较为容易实现的单轴蠕变实验，通过蠕变柔量与松弛模量之间的转换关系，可以得到基于Prony级数沥青混合料的松弛模量。

从图5中可以看出，利用配置法与最小二乘法求解得到的松弛模量曲线重合。这表明该2种方法得到的松弛模量相似度非常高。对于基质沥青混合料，500s之后的松弛模量曲线趋于稳定；对于改性沥青混合料，1 000s之后的松弛模量曲线趋于稳定。这2种方法的计算结果差别较小，因而，在实际计算过程中，推荐选用方程数量较少的配置法进行转换计算，得到基于Prony级数的松弛强度，可以利用这些参数，对沥青混合料的粘弹性能作进一步的分析。

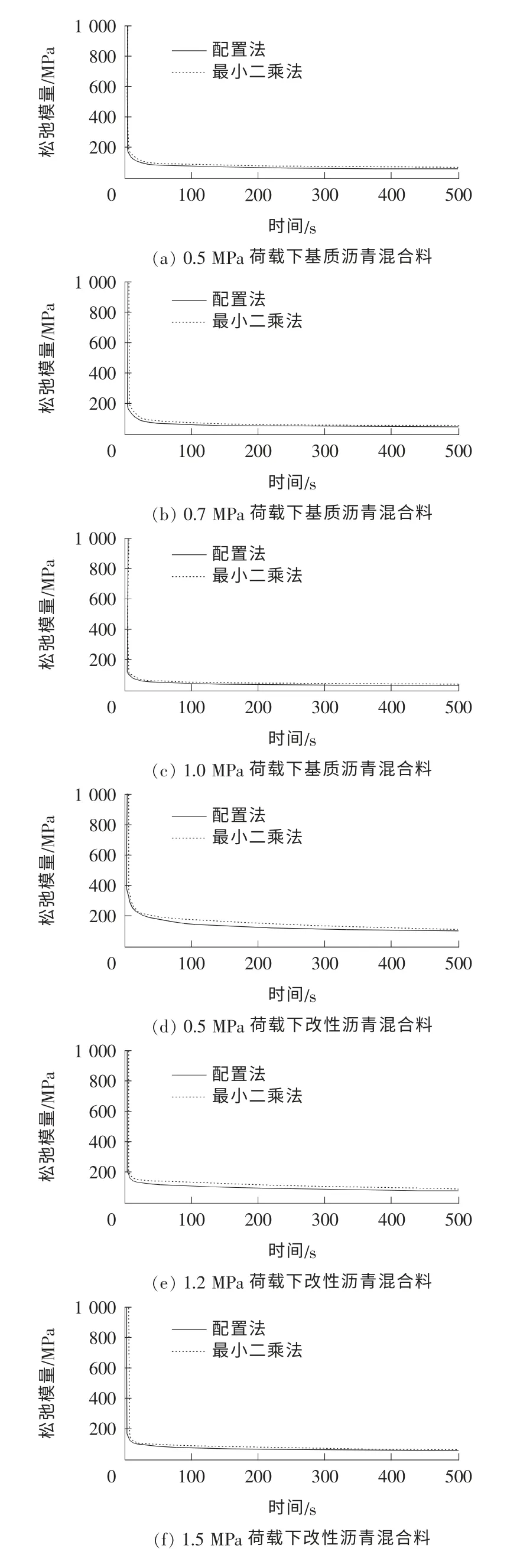
图5 不同荷载下AC－13C沥青混合料松弛模量曲线Fig.5 Relaxation modulus curves of AC－13C asphalt mixture with different loadings

5 结论

1）对基质沥青与SBS沥青两种胶结料的AC－13C沥青混合料在25℃温度环境下进行不同荷载水平的单轴静载蠕变试验。研究结果表明：不同荷载水平下的2种沥青混合料延迟强度数符合沥青混合料的蠕变性质，基于Prony级数的蠕变柔量方程的非线性拟合相关系数在0.998以上，拟合的蠕变柔量方程能较好地预测沥青混合料的蠕变性能。

2）利用拟合的蠕变柔量方程结果，根据沥青混合料松弛模量与蠕变柔量之间的转换关系，利用配置法和最小二乘法，确定蠕变柔量Prony级数方程的有关参数，计算得到的松弛模量曲线符合沥青混合料松弛性质。这表明：利用较为容易实现的单轴蠕变实验，通过蠕变柔量与松弛模量之间的转换关系，可以得到基于Prony级数的沥青混合料的松弛模量。

3）利用配置法和最小二乘法，得到的松弛模量曲线接近重合。这说明2种方法得到的松弛模量相似度非常高。该2种方法的计算结果差别较小，因而，在实际计算过程中，推荐选用方程数量较少的配置法进行转换计算。

4）基于实现容易和操作方便的蠕变实验，避免了误差较大的松弛试验。通过粘弹性参数之间的相互转换关系，得到基于Prony级数的松弛强度，可以利用这些参数，对沥青混合料的粘弹性能作进一步的分析。

（References）：

［1］张肖宁.沥青与沥青混合料的粘弹力学原理及应用［M］.北京：人民交通出版社，2006.（ZHANG Xiaoning.Viscoelastic mechanics theory and the application of asphalt and asphalt mixtures［M］.Beijing：China Communications Press，2006.（in Chinese））

［2］Monismith C L，Coetzz N F.Reflection cracking：Analysis，laboratory studies and design consideration［A］.Proceedings of Association of Asphalt Paving Technologists［C］.Chicago：［s.n.］，1980：290－293.

［3］周志刚，钱国平，郑健龙.沥青混合料粘弹性参数测定方法的研究［J］.长沙交通学院学报，2001，17（4）：23－28.（ZHOU Zhi－gang，QIAN Guo－ping，ZHENG Jian－long.Research on viscoelastic parameters determination method of asphalt mixture［J］.Journal of Changsha Communications University，2001，17（4）：23－28.（in Chinese））

［4］郑健龙，吕松涛，田小革.沥青混合料粘弹性参数及其应用［J］.郑州大学学报，2004，25（4）：8－15.（ZHENG Jian－long，LV Song－tao，TIAN Xiao－ge.Viscoelastic parameters of the asphalt mixture and its application［J］.Journal of Zhengzhou University，2004，25（4）：8－15.（in Chinese））

［5］赵延庆，唐积民，白龙.利用沥青混合料复数模量确定松弛模量研究［J］.建筑材料学报，2012（4）：498－502.（ZHAO Yan－qing，TANG Zhi－ming，BAI Long.Determination of relaxation modulus using complex modulus of the asphalt mixture［J］.Journal of Building Materials，2012（4）：498－502.（in Chinese））

［6］Yan H Q，Zhang X N，Zhang L J.Methods of fitting the Prony series of viscoelastic models of the asphalt mixture based on dynamic modulus［A］.Proceedings of the Third International Conference on Transportation Engineering［C］.Chengdu：［s.n.］，2011：1384－1389.

［7］刘孝敏，唐志平，李欣增.复柔量－蠕变柔量和复模量－松弛模量转换公式的讨论［J］.中国科学技术大学学报，1989，19（4）：476－485.（LIU Xiao－ming，TANG Zhi－ping，LI Xing－zeng.Discussion on complex compliance－creep compliance and complex modulus－relaxation modulus conversion formula［J］.Journal of China University of Science and Technology，1989，19（4）：476－485.（in Chinese））

［8］Park S W，Schapery R A.Methods of interconversion between linear viscoelastic material functions.Part I－a numerical method based on Prony series［J］.International Journal of Solids and Structures，1999，36（11）：1653－1675.

［9］张丽娟.基于蠕变试验的沥青混合料本构关系及车辙预估方法研究［D］.广州：华南理工大学，2009.（ZHANG Li－juan.Research on constitutive relations of asphalt mixtures and the method of rutting prediction based on creep tests［D］.Guangzhou：South China University of Technology，2009.（in Chinese））