基于重整化群和模糊概率法的岩土边坡稳定性

付宗志，刘 涛

（1.长沙有色冶金设计研究院有限公司，湖南长沙 410011；2.西北矿冶研究院矿山工程研究所，甘肃白银 730900）

传统的岩土边坡稳定性分析是以边坡安全系数Fs来判别边坡的稳定性。该方法具有一定的局限性，它通过数值模拟的方法得出边坡的安全系数Fs。大量的工程实践［1－5］表明，并非Fs＞1边坡就是稳定的，也不是Fs＜1边坡就会破坏。一些学者通过研究［6－9］发现，影响边坡稳定性的因素往往是随机变化的，用确定性的方法很难充分考虑岩土参数变化对边坡稳定性造成的影响。因此，有必要应用数学的方法，在考虑岩土参数随机性和模糊性的同时，对边坡的稳定性进行研究。

Logistic函数是一种常见的S形函数。Logistic映射是研究动力系统、混沌及分形等复杂系统行为的一个经典模型。Logistic映射又叫Logistic迭代，是一个时间离散的动力系统。

重整化群是一种用于解决多体问题的有力工具。该方法基于统计分形的原理，将小标尺下系统简单特性扩展到大标尺下系统复杂特性的计算，并取得了巨大的成功。重整化群已应用于地震预测、矿柱稳定性［10］、采空区安全评价［11］及采空区突水预测［12］等多个领域。

1 重整化群分析模型

1.1 重整化群简介

重整化群最早是应用于量子场论当中而得到公认。该方法通过研究系统内部组成单元之间的联系和系统单元之间的自相似变换，从宏观上对系统的一些规律进行描述，该方法是解决临界问题的有效工具。

重整化群是通过改变系统中观测尺度来获取系统参数变化规律的方法。假设系统在某个观测尺度下所获的物理参数为p，将观测尺度放大n倍，这时获得的物理参数记为p′。如果将尺寸变换函数记为fn，那么p与p′的关系为：

如果观测尺度再放大n倍，有：

如果将式（2）变成一般情况下的关系式，那么其变换函数f具有的性质为：

1.2 边坡演化的一维重整化群模型

传统的重整化群方法在研究岩石破裂时，假设一级原包由2个基本单元组成，那么一级原包中有1个及1个以上的单元破裂，则一级原包就破坏了。一级原包所有可能的情况如图1所示。一级原包发生破坏的概率为：

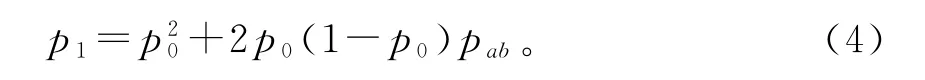
式中：p0为基本单元的破坏概率为2个单元都破坏的概率；pab为1个单元破坏后向邻近单元应力转移的条件概率，且应力向邻近为破坏的单元转移概率是相等的。

应力转移的条件概率为：

式中：pa为单元破坏前邻近单元的破坏概率；pb为单元破坏后邻近单元的破坏概率。

假设基本单元的破坏概率由Weibull分布给出，其破坏概率函数为：

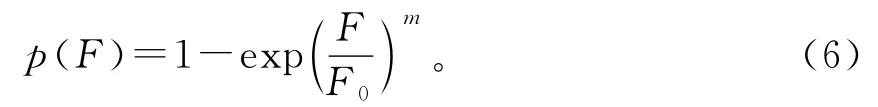
式中：F0为基本单元的强度；m为表征一级原包强度相似性的相关参数。

单元破坏后邻近单元的破坏概率为：

当m＝2时，一级原包发生破坏的概率为：

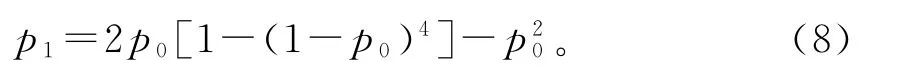
根据logistic一维映射递推关系，可得到n级原包的破坏失稳概率为：

式（9）即为一维重整化群方程，将式（9）写成函数形式：

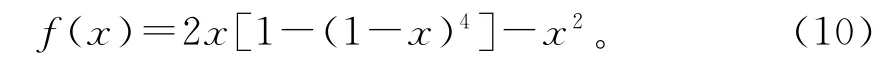
在0≤x≤1的范围内求解式（10），可得方程（10）存在3个不动点，即x＝0，0.206，1。根据判断准则，当｜（df（x）／dx）｜x＞1时，x为不稳定不动点；反之，当｜（df（x）／dx）｜x＜1时，x为稳定不动点。分别将x＝0，0.206，1带入判据df（x）／dx，得到的结果分别为：0，1.62，0。这说明0和1为稳定不动点，0.206为不稳定不动点。当x＝0时，表示没有单元破坏，系统处于稳定状态；当x＝1时，表示系统中全部单元破坏，系统处于极限不稳定状态。故x＝0.206是系统两种状态的分界点。即：当x＞0.206时，系统向不稳定的方向发展；当x＜0.206时，系统向稳定的方向发展。

图1 2个单元组成一级原包的所有可能情况Fig.1 All the possibilities of two units composed of original package

1.3 二维情况

二维情况下，1个一级原包由4个基本单元构成，2个二级原包由4个一级原包构成。与一维情况下的分析方法一致，假设p0为基本单元的破坏概率，根据式（8）可求出一级原包的破坏概率。同理，二级原包的破坏概率［12］为：

根据Logistic映射递推关系，n级原包的破坏失稳概率［13］为：

用Matlab软件求解式（12），可得x＝0.170 7为系统的临界点。

1.4 三维情况

三维情况下，1个一级原包由8个基本单元构成，1个二级原包由8个一级原包构成。假设p0为基本单元的破坏概率，根据基本单元的破坏概率，可算出一级原包的破坏概率。同理，根据一级原包的破坏概率，二级原包的破坏概率为：

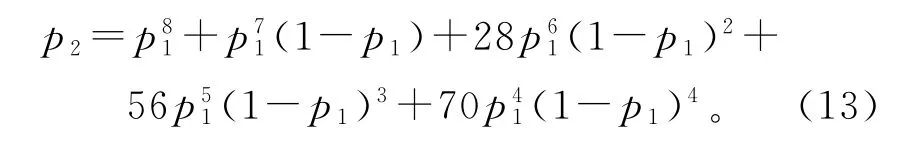
据Logistic映射递推关系，n级原包的破坏失稳概率为：

用Matlab软件求解式（14），可得x＝0.159 9为系统的临界点。

2 边坡稳定分析的模糊概率法

2.1 模糊概率

在边坡稳定性分析中，边坡的安全性用功能函数Z来表示。

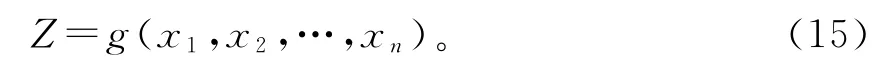
式中：xi（i＝1，2，…，n）为基本随机变量。

在模糊数学中，可将边坡失稳的概率定义为：

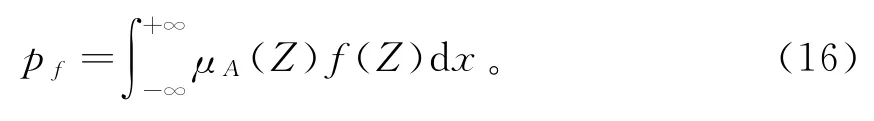
式中：pf为边坡失稳概率；μA（Z）为功能函数Z的隶属函数；f（Z）为Z的概率密度函数。

2.2 功能函数

在边坡稳定分析中，安全系数为：

式中：R为边坡的抗滑力矩；S为边坡的滑动力矩。

功能函数为：

根据瑞典条分法，安全系数为：

式中：m为边坡分条数；Wi为分条的重力；bi为分条的宽度；αi为第i个分条底部与水平方向的夹角；c为岩土的内聚力；φ为岩土的内摩擦角。

2.3 隶属函数

对于岩土边坡而言，当隶属函数越接近于1，表明边坡破坏的可能性越大；反之，隶属函数越接近于0，表明岩土边坡的破坏可能性越小。假设

结合式（20），采用分段线性分布，其隶属函数为：

2.4 概率密度函数

假设功能函数Z为非正态分布，那么可通过中心点法，求得功能函数Z的均值μZ和方差σZ。

式中：μxi为xi（i＝1，2，…，n）的均值为在中心点对功能函数求偏导数。

则概率密度函数为：

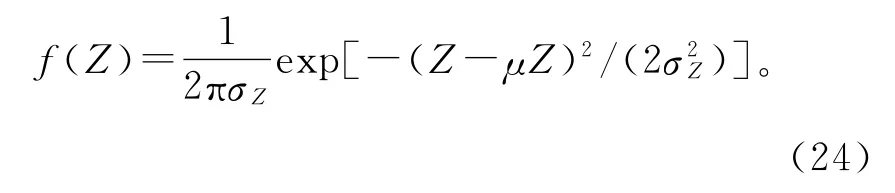
将式（24）代入式（16），可计算出边坡工程的失稳概率。对于具体的边坡工程，依据模糊概率法计算边坡的失稳概率，再与重整化群法计算出的边坡系统临界失稳概率进行比较。若其结果大于失稳概率且大于临界概率，则边坡失稳；反之，则边坡不失稳。

3 工程实例

某岩土边坡如图2所示。该滑动面滑弧半径为150m，分条数m＝8，条宽b＝10m，取内聚力c、内摩擦角φ的正切f＝tanφ为基本随机变量，随机变量的取值：E（c）为18.36，D（c）为44.5，E（f）为0.419 4，D（f）为0.003 4。

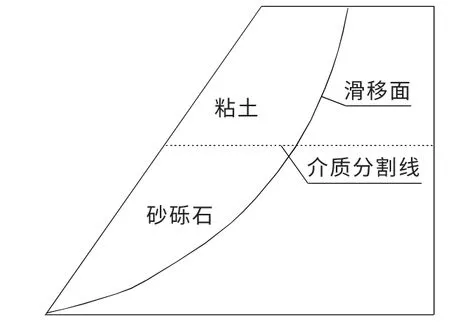
图2 边坡剖面Fig.2 Sectional view of the slope

通过中心点法计算，μZ＝0.235，σZ＝0.085，将均值μZ和方差σZ代入式（24）和式（16），得：

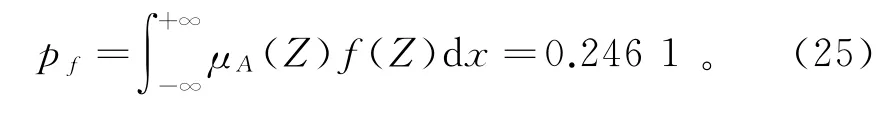
4 结论

1）根据重整化群法，建立了岩土边坡稳定性分析模型。考虑系统应力重分布对边坡稳定性的影响，将露天边坡失稳破坏的复杂问题转化为边坡失稳概率与临界失稳概率之间比较的问题，并计算得出了一维、二维及三维情况下露天边坡失稳破坏的临界概率，它们分别为0.206，0.170 7及0.159 9。

2）用模糊概率的方法对边坡的稳定性进行分析，得到了边坡失稳概率的计算方法。

3）将该方法应用于某岩土边坡稳定性分析，通过计算，得出该边坡的失稳概率为0.246 1，大于三维情况下边坡失稳的临界概率0.159 9。这说明该边坡是不稳定的，具有整体失稳的可能性。

（References）：

［1］谭晓慧.边坡稳定分析的模糊概率法［J］.合肥工业大学学报：自然科学版，2001，24（3）：442－446.（TAN Xiao－hui.The stability analysis of slope by a fuzzy probability method［J］.Journal of Hefei University of Technology：Natural Science，2001，24（3）：442－446.（in Chinese））

［2］段永伟，胡修文，吁燃，等.顺层岩质边坡稳定性极限平衡分析方法比较研究［J］.长江科学院院报，2013，30（12）：65－68.（DUAN Yong－wei，HU Xiu－wen，YU Ran，et al.Comparative study on limit equilibrium methods for the stability analysis of the bedding rock slope［J］.Journal of Yangtze River Scientific Research Institute，2013，30（12）：65－68.（in Chinese））

［3］陈建宏，王凯，钟富生.多重影响因素下的边坡稳定性评价方法及应用［J］.科技导报，2013，31（20）：20－25.（CHEN Jian－hong，WANG Kai，ZHONG Fusheng.Approach and application of rock slopes’stability assessment under the comprehensive effect of multiple factors［J］.Science ＆Technology Review，2013，31（20）：20－25.（in Chinese））

［4］丁丽宏.基于改进的灰关联分析和层次分析法的边坡稳定性研究［J］.岩土力学，2011，32（11）：3437－3441.（DING LI－hong.Research on the estimation of the slope stability based on the improved grey correlation analysis and analytic hierarchy process［J］.Rock and Soil Mechanics，2011，32（11）：3437－3441.（in Chinese））

［5］付士根.基于模糊随机可靠性的边坡稳定性评价［J］.中国安全科学学报，2012，8（8）：98－101.（FU Shigeng.Stability assessment of opencast mines slope based on the fuzzy stochastic reliability［J］.Journal of Safety Science and Technology，2012，8（8）：98－101.（in Chinese））

［6］崔建林，赵德安，余云燕，等.基于模糊概率的边坡稳定性研究［J］.兰州交通大学学报，2012，31（6）：20－23.（CUI Jian－lin，ZHAO De－an，YU Yun－yan，et al.Stability study of the slope based on the fuzzy probability［J］.Journal of Lanzhou Jiaotong University，2012，31（6）：20－23.（in Chinese））

［7］王宇，曹强，李晓，等.边坡渐进破坏的模糊随机可靠性研究［J］.工程地质学报，2011，11（9）：852－858.（WANG Yu，CAO Qiang，LI Xiao，et al.Fuzzy asymptotic theory based reliability analysis for slope progressive failure［J］.Journal of Engineering Geology，2011，11（9）：852－858.（in Chinese））

［8］刘章军，陈飞，周宜红.岩质路堑深边坡稳定性评价的模糊概率方法［J］.岩土力学，2008，29（z1）：368－372.（LIU Zhang－jun，CHEN Fei，ZHOU Yi－hong.Stability evaluation of the depth cutting slope in rock mass based on the fuzzy probability method［J］.Rock and Soil Mechanics，2008，29（z1）：368－372.（in Chinese））

［9］杨坤，周创兵，张昕，等.边坡块状结构岩体模糊随机可靠性分析［J］.岩石力学与工程学报，2006，25（2）：407－413.（YANG Kun，ZHOU Chuang－bing，ZHANG Xin，et al.Fuzzy－random reliability analysis of blocky rock mass in slopes［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（2）：407－413.（in Chinese））

［10］周子龙，李夕兵，赵国彦.民窿空区群级联失稳评价［J］.自然灾害学报，2007，16（5）：91－95.（ZHOU Zi－long，LI Xi－bing，ZHAO Guo－yan.Evaluation of the cascading collapse for private mined zone groups［J］.Journal of Natural Disasters，2007，16（5）：91－95.（in Chinese））

［11］郭生茂，刘涛，程刚，等.基于RG法的空区群矿柱临界破坏条件研究［J］.金属矿山，2014（8）：125－128.（GUO Sheng－mao，LIU Tao，CHENG Gang，et al.Pillar critical failure condition of mined－out zone groups based on RG method［J］.Metal Mine，2014（8）：125－128.（in Chinese））

［12］廖九波，邹洋，马驰，等.深部开采突水机制的细观分析和临界破坏行为［J］.中国矿山工程，2012，42（1）：66－71.（LIAO Jiu－bo，ZOU Yang，MA Chi，et al.Micromechanical analysis and critical failure actions of water－inrush mechanism in deep mining［J］.China Mine Engineering，2012，42（1）：66－71.（in Chinese））

［13］郝柏林.从抛物线谈起：混沌动力学引论［M］.上海：上海科技教育出版社，1993.（HAO Bo－lin.Starting with parabolas：An introduction to chaotic dynamics［M］.Shanghai：Shanghai Science and Technology Education Press，1993.（in Chinese））