正交各向异性介质中多方位三维转换波叠前时间偏移

黄中玉,余 波,王于静,徐亦鸣

(1.中国石油化工股份有限公司石油勘探开发研究院,北京100083;2.中国石油化工集团公司多波地震重点实验室,北京100083;3.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

正交各向异性介质中多方位三维转换波叠前时间偏移

黄中玉1,2,余 波3,王于静3,徐亦鸣3

(1.中国石油化工股份有限公司石油勘探开发研究院,北京100083;2.中国石油化工集团公司多波地震重点实验室,北京100083;3.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

目前大多数转换波叠前时间偏移(PSTM)算法只考虑了VTI各向异性介质对转换波旅行时的影响，而具有垂直裂缝的HTI各向异性介质具有较强的速度方位各向异性特点,不同传播方向的速度按照椭圆规律变化,仅使用VTI各向异性参数而不考虑速度方位变化对旅行时的影响,将导致多方位三维转换波叠前偏移成像质量下降。针对上述问题,提出一种基于正交各向异性介质的多方位三维转换波PSTM偏移算法,其转换波旅行时计算公式同时考虑了VTI和HTI各向异性参数,更加接近于地层介质的实际情况。由于转换波还受到映射在水平径向分量(R)和切向分量(T)的快、慢横波影响,因此需要在转换波叠前时间偏移之前进行R,T分量的快、慢横波分离。在常规三维转换波资料处理的基础上,利用基于正交各向异性介质的多方位三维转换波PSTM偏移算法对西南地区某实际资料进行了测试处理,结果表明,转换波叠前时间偏移结果在构造解释上更加合理,地层特征更加清晰,证实了算法的合理性和实用性。

转换波;正交各向异性介质;横波分裂;叠前时间偏移

目前有四类各向异性问题可以用地球物理技术来解决。它们分别为具有垂直对称轴的横向各向同性(VTI)、具有水平对称轴的横向各向同性(HTI)、正交各向异性(VTI+HTI)以及具有倾斜对称轴的横向各向同性(TTI)。当层状介质的地层厚度远小于地震波长时,地震波在水平和垂直方向的传播速度不同,横向速度大于垂向速度，由这种水平层状地层导致的速度各向异性称为VTI各向异性,即具有垂直对称轴的横向各向同性性质。地震波在具有定向排列垂直裂缝的地层中传播时,平行裂缝方向传播的地震波速度快、振幅能量强,而垂直裂缝方向传播的地震波速度慢、振幅能量弱，速度和振幅在不同方位上呈现椭圆性规律变化。在这种地层中横波还将发生分裂,分别以快横波速度和较强能量平行裂缝方向以及以慢横波速度和较弱振幅能量垂直裂缝方向传播。由这种垂直裂缝地层导致的方位速度各向异性称为HTI各向异性,即具有水平对称轴的横向各向同性性质。实际储层往往不只是存在单一的一种各向异性,而是两种或多种各向异性共存。特别是裂缝型油气藏,VTI+HTI组成的正交各向异性问题更为油气资源勘探开发人员所关注[1]。

对于VTI各向异性介质的转换波(PS/C波)叠前偏移技术,Dai等[2]全面阐述了如何从多分量资料中交互分析和提取纵横波垂直速度比、转换波等效速度、有效速度比及转换波各向异性参数,并在转换波各向异性参数与纵波(P)和横波(S)各向异性参数之间建立起一种联系,从而实现VTI各向异性介质的三维转换波偏移速度建模和叠前时间偏移(PSTM)处理。对于HTI各向异性介质,Grechka等[3]给出了P波NMO速度随方位角变化的基本公式,这种速度变化的趋势可以在不同方位按照椭圆规律进行拟合,当地震波传播方向与各向异性主轴方向或裂缝主方向平行时,传播速度值最大,当地震波传播方向与各向异性主轴方向或裂缝主方向垂直时,传播速度值最小。Jenner[4]提出了综合VTI和HTI各向异性的P波叠前时间偏移方法,给出了一个有效的工作流程并用实际资料进行了验证。

本文将Grechka方位各向异性速度公式扩展到转换波速度,并利用转换波速度与P波和S波速度之间的关系将转换波速度方位各向异性换算为P波和S波速度方位各向异性。在转换波偏移旅行时计算公式中,类似于Jenner同时考虑VTI和HTI各向异性参数,正确计算转换波在VTI+HTI介质中的精确旅行时,从而解决了正交各向异性介质中多方位三维转换波叠前时间偏移问题。考虑到HTI介质中的横波分裂问题,我们首先利用Alford[5]提出的基本旋转公式对水平径向分量(R)和切向分量(T)的转换波做快、慢横波分离,得到相对单一的PS1快波和PS2慢波;然后再进行转换波的VTI+HTI各向异性偏移处理,得到单一而非混合的快、慢横波波场,使成像剖面的质量得到提高,地层构造解释更加合理。

1 基本公式和理论

1.1 正交各向异性介质中转换波基本公式

对于正交各向异性介质,转换波叠前时间偏移旅行时计算同时考虑VTI和HTI各向异性参数的公式可以表述为：

(1)

式中：tPS是转换波双程旅行时;tP0是P波零偏移距的双程旅行时,tS0是S波零偏移距的双程旅行时;xP是震源点到成像点的水平距离,xS是成像点到接收点的水平距离;vP(α)是P波速度场,vS(α)是S波速度场,α是炮检方向和HTI介质主方向(裂缝主方向)之间的夹角;ηeff是P波VTI各向异性参数,ζeff是S波VTI各向异性参数。这里纵波和横波速度以及它们的各向异性参数可以由经典的转换波四参数导出,它们分别是纵、横波垂直速度比γ0和有效速度比γeff,转换波VTI各向异性参数χeff,和转换波等效速度vc。纵波、横波和转换波VTI各向异性参数与方位无关,只有速度是方位角的函数,因此我们需要解决速度随方位角变化的问题。

Grechka等[3]给出的纵波NMO速度随方位角变化的基本公式可以推广到横波和转换波的速度。我们改写转换波方位速度与快波速度和慢波速度的关系式如下：

(2)

式中：vc是与方位角有关的转换波等效速度,可以是NMO速度,也可以是偏移速度;vcfast,vcslow分别是平行和垂直HTI各向异性介质主方向(裂缝方向)的转换波等效快、慢波速度;方位角α定义为炮检方向与裂缝方向之间的夹角,即自然坐标(裂缝系统)和采集坐标之间的夹角。而转换波速度与纵、横波速度的关系则由下式确定：

(3)

式中：vP，vS和vc分别表示纵波、横波和转换波的NMO速度或偏移速度。VTI各向异性叠前时间偏移处理方法是在(1)式的偏移距高阶项中加入VTI各向异性参数项,修正转换波非双曲线旅行时,提高旅行时计算精度,从而解决中、远偏移距道集在偏移处理中出现的欠(过)偏移问题[6-7]。而HTI方位各向异性叠前偏移处理方法是通过引入速度方位各向异性参数,解决偏移速度受方位角变化影响而导致的偏移成像质量下降的问题。VTI和HTI各向异性同时存在构成了正交各向异性介质,结合(1)式、(2)式和(3)式以及转换波各向异性参数与纵、横波各向异性参数之间的关系式,即可解决转换波在正交各向异性介质中的叠前时间偏移技术问题。

1.2 横波分裂基本方程

Crampin[8]对弹性波在各向异性介质中的传播理论进行了详尽的讨论,Alford[5]在此基础上阐述了方位各向异性弹性介质中横波偏振分裂的现象,给出了由一组正交单位向量震源产生，且垂直于方位各向异性介质主轴，沿垂直方向传播的弹性波一维方程。为了更直观地解释这套理论,这里进一步解释横波分裂的现象。首先给出自然坐标系和采集坐标系的定义：由自然裂缝系统组成自然坐标系,沿平行裂缝方向传播的是快横波S1,沿垂直裂缝方向传播的是慢横波S2。由炮检方向组成采集坐标系,沿炮检方向传播的是径向分量(R分量),沿垂直炮检方向传播的是切向分量(T分量),满足右手坐标系法则。自然坐标系与采集坐标系之间的夹角称为裂缝方位角。在这种坐标系统下,采用一组正交方向的震源激发，相互垂直的水平分量接收,得到2×2C数据,Alford给出了一维弹性波在方位各向异性介质中的传播方程[5]：

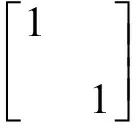
(4)

式中：e是偏微分算子,用以描述在方位各向异性介质中弹性波传播的性质和速度的时空变化;δ(z)为狄拉克函数,定义了源的空间位置;g(t)表明源的时间变化。源方向矩阵定义了一组正交性质的震源,与方位各向异性介质的自然坐标系一致。为了求解方程(1),当炮检方向的采集坐标系与方位各向异性介质的自然坐标系之间夹角为θ时,Alford的旋转矩阵[5]定义为：

(5)

对于2×2C分量数据,借助于上述旋转公式,快、慢横波分裂的基本公式可以改写为：

(6)

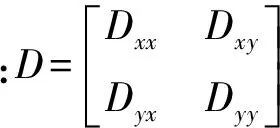
Gaiser[9]将公式(6)推广到转换波的2×2C分量,即两个正交P波震源激发,两个正交水平分量接收,得到转换横波分裂公式：

(7)

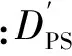
在Alford旋转矩阵的基础上还衍生出其它不同类型的转换波裂缝检测方法。本文主要关注的是,在已知裂缝方向进行快、慢横波分离后的多方位三维转换波正交各向异性叠前时间偏移成像。

2 实际资料测试处理

实际多方位三维转换波资料来自我国西南地区,三维观测系统排列片总计29片,但我们可使用的数据只有13和14排列片。图1显示了工区整个排列片分布，设计满叠加次数达160次,而13，14两个排列片数据的平均叠加次数只有25次,最高覆盖次数40次。对研究区多方位三维转换波资料进行了常规叠前预处理、转换波VTI各向异性速度分析以及转换波VTI各向异性叠前时间偏移处理。图2为三维转换波数据体在纵测线L490上进行VTI各向异性三维速度分析得到的转换波等效速度vc，纵横波垂直速度比γ0和有效速度比γe，以及转换波VTI各向异性参数χeff的VTI各向异性速度模型。图3为纵测线L490三维转换波VTI各向异性叠前时间偏移成像剖面,剖面上各反射波组信噪比高,主要反射层位基本可以在全区追踪解释。但在剖面上的方框和椭圆所示部分,整体反射波组能量较弱,连续性变差,尤其是剖面方框部分,一般认为这是受边界效应的影响所致,属于偏移处理中的正常现象。

图1 三维观测系统排列片

图2 L490线VTI各向异性速度分析得到的转换波VTI各向异性速度四参数模型

在偏移处理过程中,我们还发现偏移孔径过大会造成偏移成像效果变差,这显然是方位各向异性对偏移成像的影响所致。为此,我们尝试进行分方位角道集的处理分析,对R,T分量在0～180°按15°间隔抽取方位角道集,共计形成12个扇区的方位角道集。由于数据只有两个排列片,实际有效的方位角数据只有9个扇区。针对9个扇区数据,只需要进行转换波等效速度分析(VTI各向异性速度模型的其它3个参数不变),就能得到各个扇区的VTI各向异性速度场。用各个扇区的VTI各向异性速度模型做三维转换波VTI各向异性动校正叠加处理,将局部叠加剖面按方位角顺序依次排列,如图4所示。图4右下方叠合显示了观测系统的方位角分布图,可见数据观测的方位角呈窄带状分布,趋于北西—东南向,正东—西向的观测方位分布相对较少,因此数据在0和180°左右的方位扇区内没有足够的数据可使用,这也是为什么我们的方位角数据只显示到0～135°的原因。

图3 L490线三维转换波VTI各向异性偏移剖面

图4 方位角扇区中转换波叠加剖面(叠合显示了成像测井检测的裂缝发育方向、正北起算的扇区分布示意图、观测系统的方位角分布图)

分析图4中的叠加剖面,可以发现90°～105°扇区相对其它扇区反射波组能量最强和旅行时最短这两个重要特征。因此,可以断定该扇区方位很有可能与区域裂缝发育的主方向一致,导致在这个方向分裂的快横波具有能量强和传播速度快的特征。根据横波分裂的快、慢波偏振方向符合正交性的原则,与之成90°差异的0～15°扇区可作为慢横波偏振方向,在该扇区内转换波叠加剖面反映出反射波组能量弱、走时长的分裂慢横波的特征。而30°～45°扇区的数据基本不能成像,主要原因是数据缺失引起的成像质量差,不能真实地反映慢波的信息。在图4中部90°～105°扇区叠加剖面上叠合显示了裂缝主方向所在的扇区分布图(从正北起顺时针90°～105°红色扇区所示)。根据唐建明等[10]成像测井成果，该区裂缝发育主方向为正北90°(见图4左上角)，与本文方法得到的裂缝检测结果一致,为我们进一步开展HTI方位各向异性叠前偏移处理奠定了基础。

选择90°～105°扇区的速度作为快波速度场,0～15°扇区的速度作为慢波速度场，结合裂缝方位角参数,进行多方位三维转换波VTI+HTI正交各向异性叠前时间偏移处理,得到L490线时间偏移成像剖面，如图5所示。与图3相比,图5中反射波组的连续性和能量强度得到明显改善(图中椭圆部分所示)。特别是方框中的成像效果，在图3中被认为是由边界效应引起的波组连续性差、反射能量较弱的现象,在图5中得到明显改善。其它测线的偏移结果也得到了同样的改善[11]。但在图5所示偏移剖面上，反射波组层位增多,并且由于聚焦性好在图3中表现不明显的层位突变尖锐的现象在图5 中表现明显(见图5方框处),这在层位构造解释上不太合理。

图5 L490线三维转换波VTI+HTI正交各向异性时间偏移剖面

对于图5所示时间偏移成像剖面中反射波组层位较多的现象,分析认为是因为R分量中包含了快、慢转换横波的映射,且都有合适的速度成像所致。为此,我们利用已知的裂缝发育主方向信息对R,T分量进行转换快、慢横波分离处理,得到分离后的快、慢转换波PS1,PS2后,对快、慢转换横波进行VTI+HTI正交各向异性叠前时间偏移处理。图6为L490线三维转换快波PS1的VTI+HTI正交各向异性叠前时间偏移剖面,与图5相比，图6 最大的变化是反射层的成像时间向上抬升(见图中方框部分),为快转换波反射特征。其次,图6的波组个数有所减少,波组关系清晰,没有快、

慢转换波一起混波成像的现象,整个剖面上波组视频率有所提高。此外,图6的层位构造解释没有突变尖锐的现象,更符合地质解释的意义[12]。对分离后的PS1波用快波速度做VTI各向异性叠前时间偏移,却没有得到比图6更好的成像效果,如图7所示。图7整体上能量聚焦性稍差,但成像时间和构造形态基本一致。可见R,T分量只是在振幅上进行了投影分离,在速度上没有能够得到很好的补偿校正,因此速度模型依然适用于方位各向异性,需要用VTI+HTI正交各向异性叠前时间偏移才能获得好的成像剖面。

图8a为L490线三维转换慢波PS2的VTI+HTI正交各向异性叠前时间偏移剖面，图8b为L490线三维转换波T分量快、慢横波分离前的VTI+HTI正交各向异性叠前时间偏移剖面,对比可见分离后的转换慢波PS2成像剖面总体表现出反射能量明显减弱、旅行时增加(速度略低)的转换慢波特征。

图6 快、慢波分离后L490线三维转换快波(PS1)VTI+HTI正交各向异性时间偏移剖面

图7 快、慢波分离后L490线三维转换快波(PS1)VTI各向异性时间偏移剖面(偏移速度场采用快波速度模型)

3 结束语

多方位/全方位三维转换波资料的叠前时间偏移处理,除了需要考虑水平层状介质的VTI各向异性对转换波中、远偏移距非双曲旅行时计算的影响,还要考虑由高角度垂直裂缝导致的HTI方位各向异性对转换波速度的影响。本文提出的结合VTI+HTI的正交各向异性三维转换波叠前时间偏移方法,能够同时很好地解决这两方面的问题,明显改善了多方位三维转换波叠前时间偏移剖面反射波组的连续性和聚焦性,从而提高三维转换波叠前时间偏移成像品质。

对没有进行快、慢波分离的R，T分量偏移时，由于混合了快波PS1和慢波PS2，三维转换波VTI+HTI的正交各向异性偏移成像剖面出现了混波成像低频化、反射波组增多、反射层位旅行时降低等现象。进行快、慢波分离后再进行三维转换波VTI+HTI的正交各向异性偏移,能够明显提高成像剖面的视频率,反射波组关系清晰、反射波旅行时正确、反射波多相位的现象减少、反射界面构造解释结果具有实际地质意义。

下一步的研究工作是开展分方位扇区转换波R,T分量的VTI各向异性偏移处理,在此基础上进行快、慢转换波分裂补偿处理,并将补偿后的PS1波和PS2波以及将其返回到R,T分量的VTI各向异性偏移处理结果与正交各向异性转换波偏移处理结果进行比较,寻找多方位三维转换波叠前偏移更加合理有效的处理方案。

致谢：本文分方位角扇区的处理、各扇区速度分析、VTI各向异性速度分析以及裂缝方向分析结果来自于中国石油化工股份有限公司石油物探技术研究院多方位三维转换波资料早期处理的成果,对于能够直接应用VTI各向异性速度场、各分扇区的速度场以及裂缝方位信息进行多方位三维转换波VTI+HTI的正交各向异性偏移方法研究并发表本研究成果表示感谢！

[1] 黄中玉,孙建库,朱仕军,等.多分量地震技术[M].北京：石油工业出版社,2007:20-23

Huang Z Y,Sun J K,Zhu S J,et al.Multi-component seismic technology[M].Beijing:Petroleum Industry Press,2007:20-23

[2] Dai H C,Li X Y.Anisotropy migration and model building for 4C seismic data:a case study from Alba[J].Expanded Abstracts of 71stAnnual Internat SEG Mtg,2001,795-798

[3] Grechka V,Tsvankin I,Chen J K.Generalized Dix equation and analytic treatment of normal-moveout velocity for anisotropic media[J].Geophysical Prospecting,1999,47(2):117-148

[4] Jenner E.Combining VTI and HTI anisotropy in pre-stack time migration:workflow and data examples[J].The Leading Edge,2011,30(7):732-739

[5] Alford R M.Shear data in the presence of azimuthally anisotropy[J].Expanded Abstracts of 56thAnnual Internat SEG Mtg,1986,476-479

[6] 黄中玉,曲寿利,王于静,等.层状各向异性介质转换波克希霍夫叠前时间偏移[J].地球物理学报,2009,52(12):3109-3115 Huang Z Y,Qu S L,Wang Y J,et al.Kirchhoff prestack time migration of PS-wave data for the layered anisotropic medium[J].Chinese Journal of Geophysics,2009,52(12):3109-3115

[7] 黄中玉,王于静.一种有效的三维PS波保幅叠前时间偏移方法[J].石油物探,2014,53(4):431-436 Huang Z Y,Wang Y J.An effective 3D PS-wave true-amplitude prestack time migration method[J].Geophysical Prospecting for Petroleum,2014,53(4)：431-436

[8] Crampin S.Suggestions for a consistent terminology for seismic anisotropy[J].Geophysical Prospecting,1989,37(7):753-770

[9] Gaiser J E.Minimization of 4C Alford data matrix for non-orthogonal PS-wave reflection modes[J].68thEAEG Conference and Exhibition,2006,H039

[10] Tang J M,Huang Y,Xu X R,et al.Application of converted-wave 3D/3-C data for fracture detection in a deep tight-gas reservoir[J].The Leading Edge,2009,28(7):826-837

[11] Huang Z Y,Wang Y J.Pre-satck time migration for PS-wave data in orthorhombic symmetry media[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014,1910-1913

[12] Huang Z Y,Wang Y J.A technique to improve PS-wave image in VTI+HTI media[J].77thEAEG Conference and Exhibition,2015,N11602

(编辑：戴春秋)

Multi-azimuth 3D converted wave prestack time migration in orthotropic medium

Huang Zhongyu1,2,Yu Bo3,Wang Yujing3,Xu Yiming3

(1.SinopecExploration&ProductionResearchInstitute,Beijing100083,China;2.SinopecKeyLaboratoryofMultiComponentsSeismicTechnology,Beijing100083,China;3.SinopecGeophysicalResearchInstitute,Nanjing211103,China)

Most of the migration algorithms for converted wave prestack time migration (PSTM) only consider the VTI anisotropic medium effect.HTI anisotropic medium induced by vertical fractures has stronger azimuth velocity anisotropy,so velocity fields with different propagation directions will vary in the ellipse rule.Imaging quality of PSTM for multi-azimuth 3D converted wave data will reduce by using VTI anisotropy parameters without considering HTI anisotropy parameters in orthotropic medium.According to the above problem,we proposed a multi-azimuth 3D converted wave PSTM based on orthogonal anisotropic medium.The traveltime formula of the proposed PSTM algorithm simultaneously considers the VTI and HTI anisotropic parameters.This equation makes multi-azimuth 3D converted wave data processing closer to the actual formation medium.However,converted wave is also influenced by fast and slow shear waves mapping toR- andT-component unlike compression wave,therefore shear wave separation needs to be done forR- andT-component before converted wave PSTM in orthotropic medium.It is necessary to separate PS-wave into PS1-wave and PS2-wave fromR- andT-component in orthotropic medium for multi-azimuth 3D converted wave data.The multi-azimuth 3D converted-wave PSTM based on orthotropic medium is applied on the seismic data in Southwest China,the structure interpretation is more reasonable and characteristics of events are clearer on the results of PSTM for multi-azimuth 3D converted wave after PS1 and PS2 wave separation,which demonstrates the rationality and practicability of our algorithm.

converted wave,orthotropic medium,shear wave splitting,prestack time migration

2015-03-09;改回日期：2015-05-21。

黄中玉(1956—),男,教授级高级工程师,主要从事多分量地震资料处理方法、多波地震属性反演方法研究以及多分量处理系统研发工作。

国家科技重大专项项目(2011ZX05005-005-006)资助。

P631

A

1000-1441(2015)04-0435-08

10.3969/j.issn.1000-1441.2015.04.010