基于贝叶斯理论的孔隙流体模量叠前AVA反演

李 超,印兴耀,张广智,刘 倩,张世鑫

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中海油研究总院,北京100028)

基于贝叶斯理论的孔隙流体模量叠前AVA反演

李 超1,2,印兴耀1,张广智1,刘 倩1,张世鑫2

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中海油研究总院,北京100028)

孔隙流体模量是一种极其敏感的流体指示因子,对该参数进行地震尺度的估算在含油气储层识别中具有重要的意义。首先在孔隙弹性介质理论的指导下,推导了包含孔隙流体模量的Zoeppritz方程的线性近似方程;然后在贝叶斯理论框架下,假设先验分布服从四元柯西分布、似然函数服从高斯分布,建立了包含正则化约束的叠前AVA反演方法。模型试算结果表明,利用该方法估算孔隙流体模量,能够提高流体识别的精度;实际资料的试应用取得了较好效果,证明了该方法的有效性和实用性。

流体识别;孔隙流体模量;叠前AVA反演;贝叶斯理论

基于地震资料的储层流体识别技术始于20世纪70年代,利用高于周围振幅的强反射振幅寻找地下含气储层的“亮点”技术得到广泛应用[1-2]。1987年,Smith等[3]率先提出利用纵、横波速度相对变化量的加权叠加来判别储层含烃异常,并给出了流体因子的概念。Goodway等[4]提出了使用拉梅参数和密度进行流体指示的LMR方法。Gray等[5]消除了密度项影响,直接以拉梅参数为流体因子进行储层含流体识别。Quakenbush等[6]提出了泊松阻抗概念,通过组合纵、横波阻抗来区分岩性和流体。基于Biot-Gassmann理论,Russell等[7-8]指出流体项f可以直接作为一项流体因子参与流体检测。近些年,叠前AVO/AVA反演技术的进步极大地促进了地震流体识别技术的发展[9-11]。印兴耀等[12-13]提出利用叠前反演方法直接反演Gassmann流体项,进行精确的流体识别。宗兆云等[14]建立了利用纵、横波模量表示的孔隙弹性理论和反射系数近似方程,并发展了基于纵、横波模量反演的流体识别方法。

目前,常用的流体因子在流体识别的过程中会存在一定的误差和假象,主要是受岩石固体部分的影响[15-16]。因此要提高流体识别的精度,需要一个不受岩石固体部分影响的流体因子。孔隙流体模量Kf是表征孔隙中充填流体的抗压缩能力的物理量,它独立于岩石骨架,不受固体部分的影响,因而在指示流体性质方面有着独特的优势[17]。本文在孔隙弹性介质理论的基础上,提出了包含孔隙流体模量的Zoeppritz方程的线性近似方程;然后利用该近似方程,基于贝叶斯理论框架构建了叠前反演方法,形成了地震尺度的孔隙流体模量估算体系。

1 流体因子的提出

1.1 常规流体因子敏感性分析

基于地震资料的流体识别通常是利用流体因子对储层孔隙内的流体性质进行检测。流体因子的选择是流体识别成败的关键,因此需要一种能够充分反映孔隙流体特征的流体因子。在此,我们建立一个简单的岩石模型,在其孔隙内充填油(气)和水,并计算孔隙度变化在0～0.35，含水饱和度变化在0～1时的几种常用的流体指示因子的值,计算结果如图1和图2所示。

图1是孔隙流体为油和水混合物的情况下的计算结果。图1a至图1d中的流体因子分别是纵波阻抗、纵横波速度比、拉梅参数λ和Gassmann流体项。从图1中可以看出,如果含水饱和度一定,这几种流体因子的值都会随孔隙度的变化而剧烈变化,也就是说,这些流体指示因子的值受孔隙度的影响,而不能与含水饱和度的值一一对应,表明这几种常用的流体因子很容易受岩石固体部分的影响,不能很好地指示孔隙流体的性质。

图2是孔隙流体为气和水混合物的情况下的计算结果。图2中的情况与图1类似,几种流体因子受孔隙度影响都较大,其中图2d中含水饱和度较低时,Gassmann流体项的变化曲线近乎于直线,这是由于尺度差异造成的,若放大显示低含水饱和度部分(图2e),其变化趋势与图1d类似,这表明Gassmann流体项本身的流体敏感性高于其它几种流体因子,但是仍然会受固体部分的影响。

1.2 孔隙流体模量

这些常用的流体因子显然不适用于高精度的流体识别,因此要寻找受岩石固体部分影响小甚至不受岩石固体部分影响的流体因子。孔隙流体模量Kf是表征孔隙中充填流体的抗压缩能力的弹性参数,这是流体本身固有的性质,不受孔隙及岩石骨架的影响。图3显示的是孔隙流体模量在不同孔隙度和含水饱和度情况下的值。图3a中的孔隙流体是油和水混合物,图3b中的孔隙流体是气和水混合物。比较图3a和图3b可以看出,在含水饱和度一定时,孔隙流体模量不随孔隙度的变化而变化;而当含水饱和度变化时,孔隙流体模量相应地发生变化,因而孔隙流体模量与含水饱和度一一对应,这是理想的流体指示因子的性质。因此,若可以进行地震尺度的孔隙流体模量估计,则可以更加精确地进行储层流体识别。

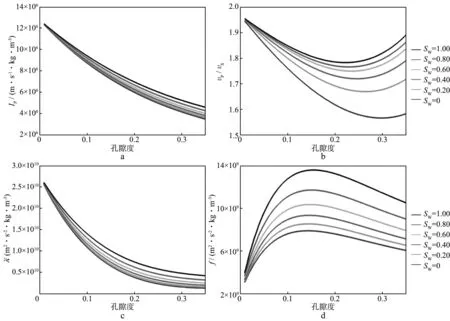
图1 流体因子随孔隙度和含水饱和度变化(流体为油和水)曲线

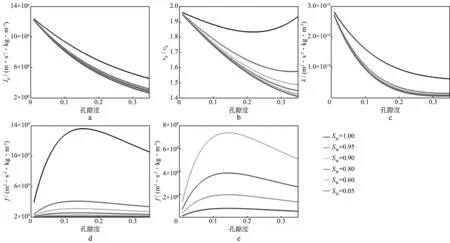
图2 流体因子随孔隙度和含水饱和度变化(流体为气和水)曲线

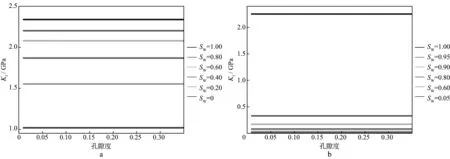
图3 孔隙流体模量随孔隙度和含水饱和度的变化曲线

2 孔隙流体模量直接反演

2.1 包含孔隙流体模量的近似方程的建立

地下岩石实际上是由固体矿物和孔隙流体组成的多孔双相介质。孔隙流体的存在必然会影响多孔岩石的力学特征,从而使介质岩石表现出一定的弹性异常。Gassmann在一系列假设前提下,研究了不排水情况下的岩石力学性质,推导了表征双相介质弹性模量参数的Gassmann方程[18]。直到现在,在基于地震信息估算岩石弹性模量方面,特别是针对碎屑岩储层来说,Biot-Gassmann理论的表现仍然最稳健,在实际应用中的使用频率也最高。Gassmann方程的表达式为：

(1)

式中：Ksat,μsat分别为饱和岩石的体积模量和剪切模量;Kf为孔隙流体模量;Kdry,μdry分别为干燥岩石体积模量和剪切模量;Km为岩石基质体积模量;φ为孔隙度。Gassmann方程的体积模量方程等式右边的第2项是流体项f,即：

(2)

Han等[19]研究了Biot-Gassmann理论中的孔隙流体与岩石骨架的固体效应对岩石模量的影响,提出由于Km≫Kf,所以有：

(3)

因此,可以得到流体项的近似表达式为：

(4)

我们将G(φ)看做一个整体,称为骨架因子G(无量纲)。假设流体项f中包含的岩石骨架矿物与孔隙度综合作用均由骨架因子G来表示(G与孔隙度φ的具体关系在此不作讨论),由(2)式近似得到(3)式的过程中产生的误差也包含在G中,因此公式(4)可以变为：

f=GKf

(5)

公式(4)在孔隙度较大时比较精确,而在孔隙度较小时会有一定的误差,并且随着孔隙度降低误差逐渐增大;公式(5)由于不是近似式,因此不会受孔隙度大小的影响。

Russell等基于Biot-Gassmann理论研究了多孔饱和流体多孔介质的AVO理论,推导了新的反

射系数近似方程：

(6)

式中：θ为平均角度;γdry,γsat分别为干岩、饱和岩石纵横波速度比;Δf/f,Δμ/μ,Δρ/ρ分别为流体项、剪切模量和密度的相对变化率。

将公式(5)代入公式(6),可得：

(7)

令η=Gμ,则：

(8)

经过简单的运算即可得到：

(9)

公式(9)就是包含孔隙流体模量的反射系数近似方程。

2.2 近似方程精度验证

为了检验推导出的AVO近似方程的精确程度,建立4个两层地层模型,模型参数如表1所示。4个模型的地层界面分别属于第1类至第4类AVO类型。针对这几个模型分别用精确的Zoeppritz方程、Russell近似方程以及公式(9)计算两个地层界面处的纵波反射系数,结果如图4所示。

图4a至图4d中的横坐标是平均角度,纵坐标是纵波反射系数。红色曲线是利用精确Zoeppritz方程计算的结果,粉色点线是利用Russell近似方程计算的结果,蓝色点线是利用公式(9)计算的结果。从图4中可以看出,采用公式(9)计算的精度与采用Russell近似方程计算的精度接近。对于第1,2,3类AVO模型,采用公式(9)计算的精度接近于采用精确Zoeppritz方程计算的精度;计算第4类AVO模型时,在角度较小时(小于30°),采用公式(9)计算的精度较高,随着角度的增加,与采用精确Zoeppritz方程计算的误差逐渐增大。总的来说,公式(9)的精度能够满足地震反演的需求。

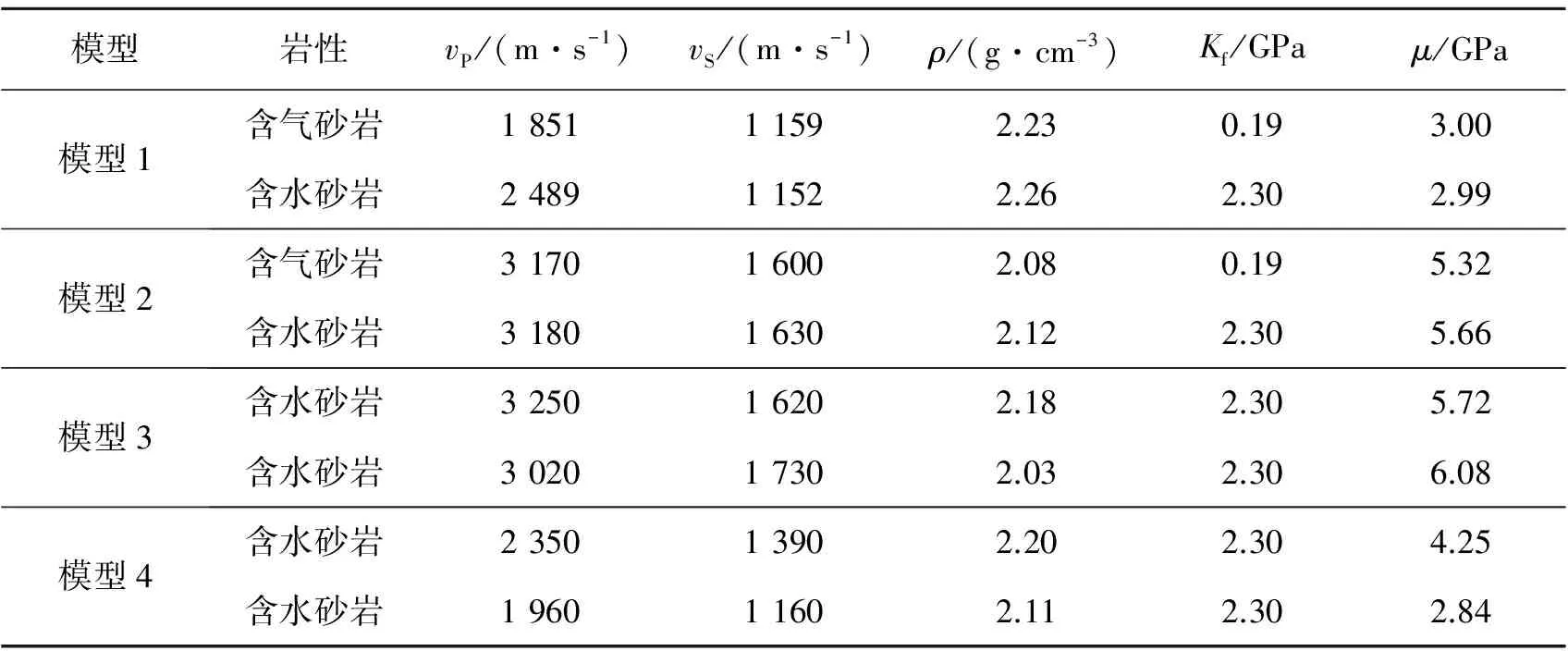
表1 模型参数

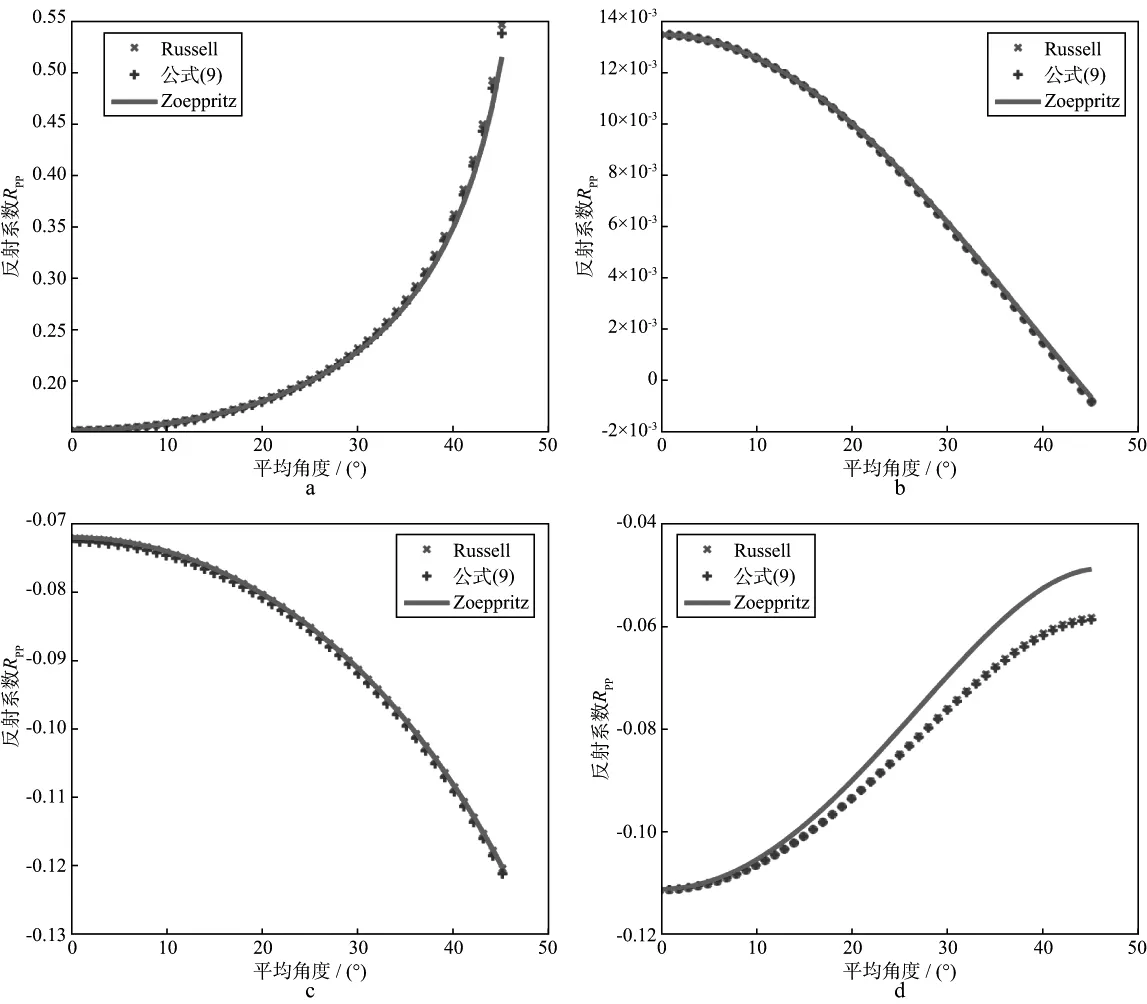
图4 采用不同模型计算的纵波反射系数

2.3 测井尺度孔隙流体模量估计

在实际应用中,无法利用常规的测井方法直接测量孔隙流体模量Kf和骨架因子G,因此需要根据岩石物理理论进行间接计算。有多种可以用来计算孔隙流体模量的方法,本文选取基于岩石物理建模的计算方法。在Gassmann方程中,若可以准确的计算出饱和岩石体积模量、干燥岩石体积模量以及岩石基质的体积模量等参数,就可以准确的计算孔隙流体模量Kf。

计算岩石基质的模量最常用的方法是VRH理论。Voigt模型提出的N种矿物组成的复合介质的有效体积模量KV的计算公式为：

(10)

式中：KV是Voigt有效体积模量;fi是第i种组分的体积分量;Ki是第i种组分的体积模量。Voigt有效体积模量代表上边界,利用Reuss模型给出有效体积模量的下边界ＫＲ：

(11)

利用Voigt-Reuss-Hill平均得到岩石基质的体积模量：

(12)

干岩石体积模量Kdry和岩石基质体积模量Km的关系可以通过建立岩石物理模型得到。岩石物理模型需要根据实际储层特点建立,这里假设所研究的储层为典型的砂泥岩储层,以最为常用的Xu-White模型[20]为例进行计算。

Keys和Xu提出了砂岩的干岩石体积模量的表达式[21]：

(13)

由测井资料可以获取纵、横波速度以及密度信息,在此基础上根据方程(14)可以得到饱和岩石体积模量：

(14)

利用公式(12)至公式(14)得到饱和岩石体积模量Ksat,干燥岩石体积模量Kdry和岩石基质体积模量Km后,结合公式(1)即可求得测井曲线对应的孔隙流体模量曲线;然后,将孔隙流体模量带入公式(5) 即可得到骨架因子G。

(15)

(16)

2.4 基于贝叶斯理论的AVA反演

叠前AVA反演需要综合地质、测井和地震资料,它以包含丰富地下信息的叠前地震反射资料为主要资料,以地质和测井资料作为约束,来揭示地下储层的属性及其含流体特征。为了更好地利用待反演参数的先验信息和提高反演结果的合理性,本文采用基于贝叶斯理论的AVA反演方法。

由于地震数据是4个不同角度的部分角度叠加道集,因此公式(9)按照入射角不同,以矩阵形式表示为：

(17)

考虑n个界面的情况,将矩阵进行块化处理并加入子波矩阵,得到：

(18)

(18)式可简记为：

Gm=d

(19)

基于贝叶斯理论得到的反射系数的后验概率密度函数可表示为：

(20)

式中：d表示部分角度叠加地震数据;m表示待反演角度反射系数;P(m|d)表示后验概率密度函数;P(d|m)表示描述数据d和反射系数m之间关系的似然函数;P(m)是先验概率密度函数;P(d)表示边缘分布,在只考虑后验分布的形状时,其数值可以取常数。

假设地震资料背景噪声服从高斯分布,地震数据和反射系数之间的关系可以用服从高斯分布的似然函数来描述,即

(21)

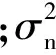
由于柯西分布能够突出小反射系数,能提高反演结果的分辨率,因此,假设先验信息服从柯西分布。考虑到各待反演参数之间的相关性,这里采用四元柯西分布：

(22)

式中：N为地震数据样点数;Φi=(Di)TΨ-1Di;Ψ是一个4×4的系数矩阵,Ψ需要使用最大期望(Expectation Maximization,EM)算法计算;Di是4×4N的矩阵,定义为：

(23)

由贝叶斯公式可以得到后验概率密度分布为：

(24)

将(24)式代入边缘化公式,取对数后得到最大化后验概率分布目标函数为：

J(m)=JG(m)+JCauchy(m)

(25)

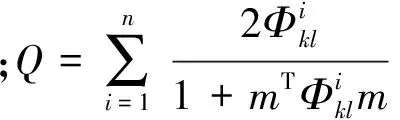
(25)式通过柯西先验分布加入稀疏约束,在压制噪声影响的同时,提高了反演结果的稀疏性。但是，由于地震资料是带限的,所以反演结果也是带限的。为了改善反演剖面的横向连续性,提高反演结果的预测精度,通过加入平滑正则约束项和点约束项,对反演结果低频分量进行补偿。

为了对反演结果低频分量进行补偿,在目标函数中加入平滑正则约束项和点约束项,得到

(26)

式中：平滑正则约束项JSmooth(m)=α‖C1m-ξ1‖2;点约束项JPoint(m)=β‖C2m-ξ2‖2。其中,α,β为加权系数,控制约束信息的相对使用量。可以看出,平滑正则约束项和点约束项的数学表达式相同,但物理意义却不同,主要体现在积分矩阵C的构建上。在平滑正则约束项中,C1和ξ1是由反射系数序列时间采样点的数目和低频模型或非常平滑单井模型计算得到;而在点约束项中,C2和ξ2是由约束点的位置和对应位置处测井数据或井插值数据计算得到。

因此,(26)式即为最终的目标函数,对目标函数求梯度并令其等于0,得到反演方程：

(27)

式中：λ为加权系数。

从(27)式所示的反演方程可以看出,该方程有一定的弱非线性性,因此采用重加权迭代最小二乘算法进行求解即可得到各项的相对变化量,再进行积分即可得到最终结果。

反演流程如图5所示。

图5 基于贝叶斯理论的AVA反演流程

3 模型试算

为验证本文方法的可行性和稳定性,用某实际工区的井数据建立模型进行试算。利用实际测井资料计算得到的模型曲线如图6所示。采用主频为35Hz的雷克子波和精确Zoeppritz方程进行正演模拟得未加噪声的合成地震记录(图7)。

图6 用于模型试算的井数据

图7为未加噪声的合成地震记录。通过合理的角度分析进行叠加得到部分角度叠加道集,然后利用本文提出的反演方法实现孔隙流体模量反演。图8为无噪声合成数据反演结果，图中实线表示模型的值,虚线表示反演结果。反演结果表明,无噪声情况下,该方法获取的孔隙流体模量与真实值吻合程度较高。

图7 未加噪声的合成地震记录

图8 未加噪声合成地震记录的反演结果

为了进一步检验该方法的稳定性,对合成地震记录中加入信噪比为2∶1的高斯随机噪声,图9是加入噪声后的合成地震记录。同样,经过角度分析进行叠加得到部分角度叠加道集并进行孔隙流体模量反演。图10是在地震数据中加入高斯随机噪声(信噪比为2∶1)后的反演结果。从图10中可以看出,孔隙流体模量反演结果仍与模型值基本吻合,但密度项的误差相比其它3项略大,这是因为密度项的系数权值低,因而对反射系数的影响相对较小;其它两个参数的反演结果也较为准确,从而证明该方法具有一定的抗噪性。

图9 加入信噪比为2∶1的高斯随机噪声后的合成地震记录

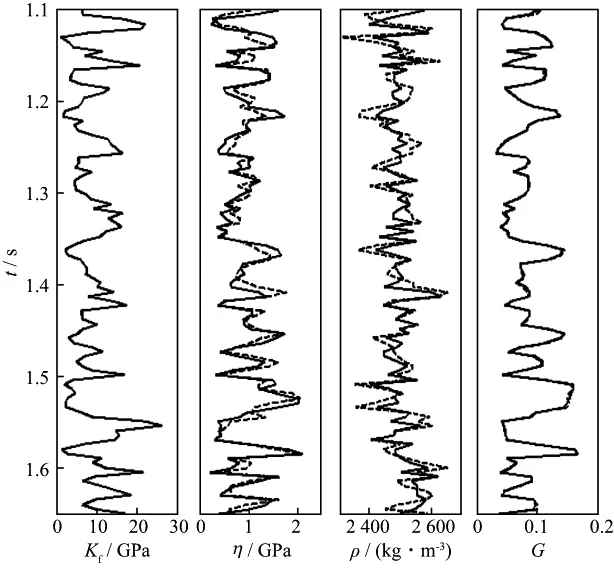
图10 加入信噪比为2∶1的高斯随机噪声后的反演结果

4 实例应用

将本文所述方法应用于中国东部某油田的实际资料。在进行叠前地震反演之前,需要对地震数据进行保幅处理,包括精细的波前扩散补偿、震源组合与检波器组合效应的校正、反Q滤波、地表一致性处理、叠前去噪处理、去除多次波等,并假设处理后的层间多次波、各向异性的影响可以忽略不计。由于输入地震数据是部分角度叠加道集,所以要根据已知的速度信息,将叠前CMP或CRP道集转换到角度域,再根据实际入射角范围,进行分角度叠加。图11是由小到大的4个角度部分叠加剖面。图中,在CDP55处有一口井(A井),紫色直线是A井的井轨迹,井轨迹处的柱状体表示测井解释成果,其中,蓝色部分表示非储层,绿色部分表示含水砂岩,红色部分表示含油砂岩;深度为1.56s处有一套含水储层,1.58s处有一套含油储层。首先利用常规反演方法反演得到Gassmann流体项f(图12a),从图12a中可以看出,在两个储层位置均有低值异常显示,但是含油储层和含水储层的异常值一样,无法区分。然后利用本文提出的反演方法实现孔隙流体模量反演Kf(图12b),从图12b中可以看出,在两个储层位置均有低值异常显示,而且含油储层的值比含水储层的值更低,可以进行区分。该反演结果与岩石物理分析结果以及实际钻井结果吻合,从而证明了方法的实用性和优越性。

图11 不同中心角度的叠加道集剖面

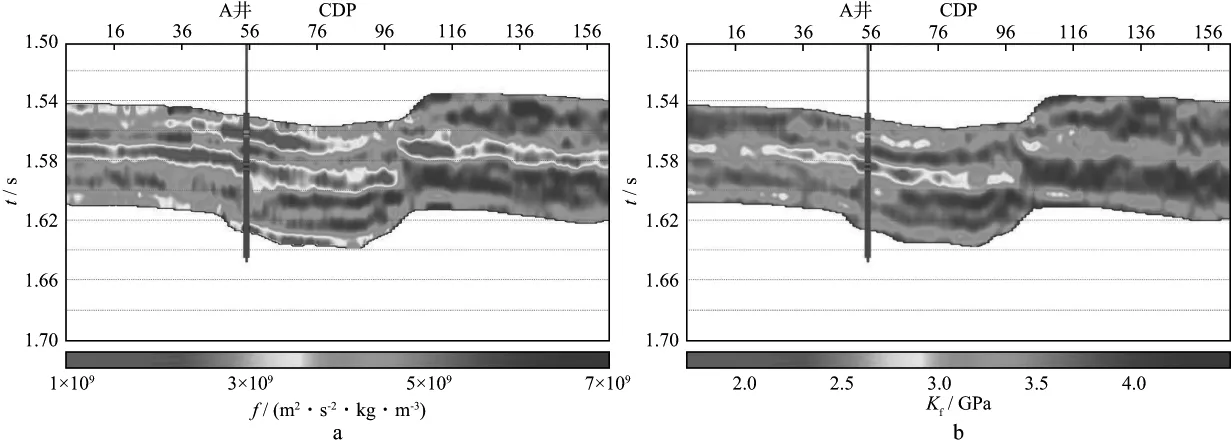
图12 叠前AVA反演结果剖面

5 结论与讨论

储层流体识别是地震勘探的重要目标之一,孔隙流体模量作为独立的流体指示因子,不受岩石固体部分的影响,流体敏感性高。本文在孔隙弹性介质理论的基础上,提出利用孔隙流体模量作为流体因子,并推导了包含孔隙流体模量的Zoeppritz方程的线性近似方程。在贝叶斯理论的框架下,以柯西分布作为先验分布,高斯分布作为似然函数,建立了相应的叠前AVA反演方法。利用该方法进行叠前反演可以直接估算孔隙流体模量,提高储层流体识别的精度。模型试算可以看出该方法精度高,而且有一定的抗噪性。将其应用于实际工区资料反演,流体识别效果很好,说明了该方法应用于实际生产的可行性。

[1] Backus M M,Chen R L.Flat spot exploration[J].Geophysical Prospecting,1975,23(3):533-577

[2] Ostrander W J.Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence[J].Geophysics,1984,49(10):1637-1648

[3] Smith G C,Gidlow P M.Weighted stacking for rock property estimation and detection of gas[J].Geophysical Prospecting,1987,35(9):993-1014

[4] Goodway B,Chen T,Downton J.Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters： “λρ”,“μρ”,“λμfluid stack”,from P and S inversions[J].Expanded Abstracts of 67thAnnual Internat SEG Mtg,1997,183-186

[5] Gray D,Goodway B,Chen T.Bridging the gap:using AVO to detect changes in fundamental elastic constants[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999,852-855

[6] Quakenbush M,Shang B,Tuttle C.Poisson impedance[J].The Leading Edge,2006,25(2):128-138

[7] Russell B H,Hedlin K,Hilterman F J,et al.Fluid-property discrimination with AVO:a Biot-Gassmann perspective[J].Geophysics,2003,68(1):29-39

[8] Russell B H,Gray D,Hampson D P.Linearized AVO and poroelasticity[J].Geophysics,2011,76(3):C19-C29

[9] Buland A,Omre H.Bayesian linearized AVO inversion[J].Geophysics,2003,68(1):185-198

[10] Downton J E.Seismic parameter estimation from AVO inversion[D].Calgary:University of Calgary,2005

[11] Yin X Y,Yang P J,Zhang G Z.A novel prestack AVO inversion and its application[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,2041-2045

[12] 印兴耀,张世鑫,张繁昌,等.利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J].石油地球物理勘探,2010,45(3):373-380 Yin X Y,Zhang S X,Zhang F C,et al.Utilizing Russell approximation based elastic wave impedance inversion to conduct reservoir description and fluid identification[J].Oil Geophysical Prospecting,2010,45(3):373-380

[13] 印兴耀,宗兆云,吴国忱.非均匀介质孔隙流体参数

地震散射波反演[J].中国科学:地球科学,2013,43(12)：1934-1942 Yin X Y,Zong Z Y,Wu G C.Seismic wave scattering inversion for fluid factor of heterogeneous media[J].Science in China:Earth Sciences,2013,43(12)：1934-1942

[14] 宗兆云,印兴耀,吴国忱.基于叠前地震纵横波模量直接反演的流体检测方法[J].地球物理学报,2012,55(1)：284-292 Zong Z Y,Yin X Y,Wu G C.Fluid identification method based on compressional and shear modulus direct inversion[J].Chinese Journal of Geophysics,2012,55(1)：284-292

[15] 张世鑫.基于地震信息的流体识别方法研究与应用[D].青岛：中国石油大学(华东),2012 Zhang S X.Methodology and application of fluid identification with seismic information[D].Qingdao:China University of Petroleum,2012

[16] 印兴耀,曹丹平,王保丽,等.基于叠前地震反演的流体识别方法研究进展[J].石油地球物理勘探,2014,49(1)：22-34 Yin X Y,Cao D P,Wang B L,et al.Research progress of fluid discrimination with pre-stack seismic inversion[J].Oil Geophysical Prospecting,2014,49(1)：22-34

[17] 印兴耀,李超,张世鑫.基于双相介质的地震流体识别[J].中国石油大学学报(自然科学版),2013,37(5):38-43 Yin X Y,Li C,Zhang S X.Seismic fluid discrimination based on two-phase theory[J].Journal of China University of Petroleum (Edition of Natural Sciences),2013,37(5):38-43

[18] Gassmann F.Uber die elastizitat,poroser medien[J].Vierteljahrsschrift der Natruforschenden Gesellschaft in Zurich,1951,96：1-23

[19] Han D H,Batzle M.Gassmann’s equation and fluid-saturation effects on seismic velocities[J].Geophysics,2004,69(2)：398-405

[20] Xu S,White R E.A new velocity model for clay-sand mixtures[J].Geophysical Prospecting,1995,43(1):91-118

[21] Keys R G,Xu S Y.An approximation for the Xu-White velocity model[J].Geophysics,2002,67(5):1406-1414

[22] Eshelby J D.The determination of the elastic field of an ellipsoidal inclusion and related problems[J].Proceedings of the Royal Society of London,1957,241(1226):376-396

(编辑：顾石庆)

Prestack AVA inversion for pore fluid modulus based on the Bayesian theory

Li Chao1,2,Yin Xingyao1,Zhang Guangzhi1,Liu Qian1,Zhang Shixin2

(1.CollegeofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China; 2.CNOOCResearchInstitute,Beijing100028,China)

Pore fluid modulus is an extremely sensitive fluid indicator.It is significant to estimate pore fluid modulus for reservoir fluid discrimination in seismic scale.Based on the poroelastic theory,a Zoeppritz approximation equation containing the pore fluid modulus is derived.Then in the theoretical framework of Bayesian theory,we assume that the prior distribution can be modelled via the four-variable Cauchy distribution and the likelihood function follows the Gaussian distribution.The objective function of prestack AVA inversion is constructed containing the regularized constraint.A synthetic data test shows that the estimation of pore fluid modulus with this method improves the accuracy of fluid identification,and the application results of actual seismic data demonstrates its effectiveness and practicability.

fluid discrimination,pore fluid modulus,prestack AVA inversion,Bayesian theory

2014-11-12;改回日期：2015-01-29。

李超(1987—),男,博士,主要从事储层预测和流体识别方面的研究工作。

国家重点基础研究发展计划(973计划)项目(2013CB228604,2014CB239201)、国家油气重大专项(2011ZX05014-001-010HZ)、中国石油科技创新基金项目(2011D-5006-0301)、中央高校基本科研业务费专项资金项目(11CX06003A)共同资助。

P631

A

1000-1441(2015)04-0467-10

10.3969/j.issn.1000-1441.2015.04.014