裂缝性孔隙介质频变AVAZ反演方法研究进展

刘喜武,董 宁,刘宇巍

(中国石油化工股份有限公司石油勘探开发研究院,北京100083)

裂缝性孔隙介质频变AVAZ反演方法研究进展

刘喜武,董 宁,刘宇巍

(中国石油化工股份有限公司石油勘探开发研究院,北京100083)

由于尺度的限制,利用地震方法进行裂缝参数定量表征一直是地球科学的难题。基于裂缝性孔隙介质动态等效理论的频变AVAZ反演方法给出了研究思路。首先介绍了裂缝性孔隙介质的等效介质理论研究进展,分析比较了各种裂缝性储层岩石静态等效介质模型和动态等效介质模型;然后给出了基于Chapman模型的裂缝参数和渗透率定量表征的正问题数学模型以及反演问题求解的方法和策略,以及基于模型数据的数值计算结果;最后讨论了频变AVAZ反演方法目前存在的问题和进一步研究方向。

多尺度裂缝;频率依赖地震各向异性;AVAZ;裂缝参数;定量反演

世界油气勘探开发实践表明,几乎所有的油气藏都和裂缝有关,超过60%的油气藏可以归结为裂缝型油气藏[1]。裂缝在大多数碳酸盐岩和非常规致密油气、页岩油气储层中具有至关重要的作用,为储层提供了基本的存储空间和运移通道。天然裂缝控制致密低渗透油气藏的成藏过程、富集规律、单井产能及开发方式,更是非常规页岩油气形成“甜点”的关键要素。裂缝型油藏管理的关键举措就是对裂缝储层的地质、地球物理、油层物理参数进行精确的描述与建模[2],裂缝的预测和定量表征是基础和关键。随着国内外大量裂缝型油藏的发现与开发,专家学者对于裂缝性储层裂缝参数的描述和裂缝分布的预测进行了大量的研究,取得了一些进展[2],包括野外露头描述地质学方法、实验室岩心分析方法和成像测井、在产油田类比法、测井评价方法(井筒斯通利波、PEF测井、声波和密度测井、漏失循环、钻孔崩塌、偶极子声波测井等)、地震预测方法、利用动态生产数据预测裂缝、裂缝尺寸和开度分布的地质统计学方法等等。然而,由于裂缝发育的非均质性强、目标难确定、数据的尺度限制和融合困难等原因,裂缝性油气藏勘探成功率仅30%～40%,地层围压条件下裂缝的定量预测和评价仍是世界级的难题,裂缝预测和定量表征问题的解决依然任重道远,特别是地震、测井和地质等不同尺度裂缝预测方法的多尺度融合尚无明确思路。

由于地震裂缝预测方法的横向分辨能力和空间展布预测优势,在裂缝系统识别、裂缝性储层预测和精细描述技术中具有重要地位,得到广泛而深入的研究。但是,由于地震波分辨尺度的限制,目前地震方法裂缝定量预测和描述还在探索之中。地震裂缝预测主要有三类方法,适应不同的裂缝尺度:一是叠后地震几何属性[3],如曲率、相干、不连续性、蚂蚁追踪等,主要适用于裂缝展布尺寸大于地震波长的宏观尺度断层级别的裂缝,表现为地震同相轴的错断;二是叠前地震绕射波成像方法[4],属于新兴的技术,主要适用于裂缝尺度与波场差不多的群集裂缝,利用绕射波场进行成像,进行断点和裂缝分布直接成像;三是利用叠前地震数据(方位)各向异性的裂缝预测[3],主要针对裂缝尺度小于地震波长的弥散裂缝预测,通过P波或S波地震各向异性分析,定性描述裂缝强度和裂缝方位,或定量反演裂缝参数。对于利用地震叠前各向异性方法识别小于波长尺度裂缝的能力,地球物理学界开展了广泛而深入的研究,特别是P波各向异性裂缝预测方法,该方法是本文阐述的重点。

利用地震各向异性进行复杂裂缝系统的预测也要遵从一般物理系统研究的程序:裂缝系统建模与模型参数化,物理规律描述即正问题建立,裂缝系统参数的反演。随着地震采集技术的进步(宽/全方位),从裂缝岩石物理建模、正演模拟、各向异性属性椭圆拟合定性预测裂缝,到含流体裂缝性孔隙介质裂缝储层参数定量反演的频变AVAZ方法,即多尺度裂缝频率依赖地震各向异性定量表征方法,取得了重要的进展。鉴于纵波三维地震应用的广泛性和经济性,本文仅对裂缝性孔隙介质地震P波AVAZ裂缝预测和流体识别方法的研究进展和发展趋势进行阐述分析,论述多尺度裂缝频率依赖AVAZ定量表征方法的研究进展,包括裂缝性孔隙介质岩石物理建模与弹性性质分析、频变AVAZ分析与裂缝参数定量反演。

1 裂缝性孔隙介质的等效介质理论

岩石物理理论一般可以划分为三大类[2]:①不详细描述微观非均匀性(如孔隙形状、孔隙连通性和流体分布等)的非均匀岩石的宏观模型,Biot-Gassman理论及其众多的扩展(如双孔隙模型)当属此类;②基于包含的模型,从微观特征的描述(包括孔隙几何特征和流体分布)到预测非均匀岩石的宏观弹性性质和水动力特性,Hudson模型、Xu-white模型、Chapman模型都属于此类,描述复杂的裂缝性储层需要采用此类理论和方法;③包括岩石在内的合成材料物理特性的边界模型,如Voigt-Reuss边界和Hashin-Shtrikman边界。

由于裂缝具有复杂的地质特征,对裂缝性孔隙介质进行详细的微观描述需要众多参数,很多参数无法从地球物理响应中观测,或者没有地震响应。为了模拟裂缝性介质的地震波响应,采用“等价介质表示”或“等效介质理论”,把复杂的裂缝性介质从数学上用一种均匀介质代替,但是两者具有相同的宏观地震响应特征,也称为裂缝性岩石等效介质建模。裂缝型储层等效介质模型建立起了地震数据与储层特征之间的联系。

传统的裂缝等效介质模型,也称静态等效介质理论,未考虑岩石孔隙和流体的存在,反映裂缝在长波长极限(低频极限,与频率变化无关)地震数据的响应,各向异性分析只能定性推断方位上裂缝的走向和裂缝密度(发育强度)的空间分布,但是无法定量获得裂缝几何结构细节信息(如裂缝尺寸、裂缝开度等),因为基于静态等效介质模型的地震各向异性分析对这些裂缝参数不敏感[5]。采用基于地震各向异性理论发展起来的技术进行裂缝系统的识别和描述在过去30余年里取得了长足的进步,提出很多技术,用于估计裂缝的方位和密度,并实际应用中取得了一定的效果,如AVAZ技术,其中地震各向异性与裂缝性储层裂缝参数的联系就是通过静态等效介质理论建立的。

裂缝性储层中的细观尺度裂缝在地震频段可引起重要的地震波频散和衰减,研究地震各向异性的频率依赖特性,可以定量获得裂缝参数的有关信息(如裂缝尺寸和开度)和流体饱和度,进而获得裂缝性储层的渗透率分布[5],这就需要发展能够描述全频段内裂缝型储层岩石中地震波传播特性的频率依赖的“动态等效介质模型”。

1.1 裂缝性储层岩石静态等效介质模型

在地震波长远大于裂缝长度和间距(长波长极限)假设条件下,微观局部非均匀裂缝岩石可用一种等价的宏观均匀介质来表示。如果非均匀或裂缝是定向排列的,等价均匀介质的平均弹性性质则为各向异性。大多数裂缝储层岩石介质等效模型假设是频率(尺度)独立的,不能区分微裂隙、地层尺度或中尺度(均小于地震波长)的裂缝。

Hudson模型是孤立的裂缝模型[6]。Hudson理论基于对弹性固体介质中具有薄硬币状椭圆裂隙或包含物情况下平均地震波场的散射理论分析(平滑方法),等效弹性常数刚度张量表示为:

(1)

其中，c(0)是无裂缝各向同性背景岩石的弹性常数张量,c(1)和c(2)为考虑裂隙之间相互作用一阶和二阶校正量,e为地球物理定义的裂缝密度,定义为:

(2)

式中：N为裂隙的数目；V是裂隙的体积,令γc=N/V,称为数密度,即单位体积的裂隙数量；a是裂隙的长轴半径；φ为裂隙孔隙度；α为裂隙的横纵比。对于地层限制裂缝,其密度定义为:

(3)

式中：H为裂缝层的裂缝高度；L为裂缝长度；S为裂缝间距。Hudson模型已被Hudson和合作者们拓展为更为宽泛的裂缝分布情形,由于其简单灵活,目前仍是工业界和学术界使用最为广泛的裂缝模型之一。

另一类裂缝等效介质模型,称为滑动界面或位移不连续性模型,又称线性滑移理论,以Schoenberg最为著名[7],实际上是众多研究者的贡献。这类模型忽略裂缝的形状和微小结构,假设裂缝是一个被二维无限面包围着的薄层,即在理想状态下将裂缝看作为一个零厚度的平面,假设与裂缝附近未扰动的岩石相比,跨越裂缝的应变则非常大,至少要大一个数量级,跨越裂缝面的位移与作用于裂缝面上的应力呈线性关系,且位移不连续,但旋转不变。裂隙应变与应力之间满足:

(4)

式中：ε为裂隙介质的平均应变张量；σ为裂隙介质的平均应力张量；S0无裂缝均匀介质基质的柔度张量；Sf为由于裂隙存在引起的额外柔度张量。

最初的Hudson理论和线性滑移理论,都是假设裂隙嵌入不含孔隙的单一固体均匀弹性介质中,没有考虑孔隙存在对地震波传播的影响,此后Hudson理论和线性滑移理论均有较大的改进和发展[2]。

Thomson等径孔隙模型[8],考虑一组定向裂缝与等径孔隙之间的流体流动作用,给出低频和中高频两种情况下各向异性参数及弹性参数柔度矩阵的表达式。低频情况下,在地震波半个周期内,流体的压力有足够的时间达到完全平衡,岩石处于松弛极限状态,这时该模型预测的地震波传播特性与各向异性Gassmann方程[9]一致。中高频情况下,在地震波半个周期内,流体来不及流动,流体流动效应可以忽略,裂缝等价于孤立情况,岩石处于非松弛极限状态,这时该模型预测的地震波传播特性与Hudson模型[6]中孤立裂缝状态一致。为克服Hudson模型和Thomson模型对裂缝的硬币形状且稀疏分布的假设,Gurevich利用线性滑动模型和各向异性Gassmann方程,直接由非裂缝性孔隙岩石的弹性参数和干裂缝岩石的裂缝柔度参数,推导出裂缝性孔隙介质的等效弹性模量[10],对裂缝的形状和密度没有限制,在描述含定向裂缝的流体饱和岩石的弹性性质方面与Thomson等孔隙模型具有等价性。

Jackobsen等[11-12]提出T矩阵方法来模拟渗透率,也属于一种静态等效介质模型。

静态等效介质模型描述的都是高频段或低频段极限情况下裂缝性储层岩石的弹性响应,换句话说,就是与频率变化无关,只能得到裂缝密度和裂缝走向信息。众多来自裂缝性储层的地震数据表明,实际储层中地震波会发生较强的速度频散,也就是储层的弹性响应具有频率依赖性,发展能够描述裂缝性储层岩石地震波传播特性的全频段动态等效介质理论和模型不但可以获得裂缝密度和方位的信息,还可以描述多尺度裂缝的几何尺寸的细节信息,如裂缝的长度和开度等,对于渗透率的预测十分重要。

1.2 含流体裂缝性孔隙介质岩石动态等效介质模型

裂缝性储层岩石实际上是一种含流体裂缝性孔隙介质,由于孔隙和流体的存在以及孔隙中流体和裂缝中流体之间的流动作用,对地震波的传播特性具有重要影响,当孔隙度较大时(大于8%),影响更为显著。能够同时考虑细观尺度裂缝(Fracture)、微观裂隙(Crack)、背景介质的孔隙微观结构以及地震波传播过程中裂缝与孔隙之间流体的流动作用的等效介质理论模型，可以更精细有效地描述实际裂缝性储层岩石,基于此类模型建立的正演和反演方法,才能更好地定量表征裂缝参数(裂缝开度、长度、裂缝密度和走向)和流体性质。

Hudson等考虑连通裂隙之间以及裂隙与等径孔隙之间的流体流动,发展了一种能够考虑全频段内地震波传播特性的动态等效介质模型,弹性模量表达式为频率的连续函数[13]。高频极限时,与Thomsen等径孔隙模型等价,在低频极限时与Thomsen等径孔隙模型及各向异性Gassmann方程不一致,因此不能在全频段内有效。

Parra[14]结合孔隙弹性BISQ(Biot-Squirt)模型和Thomson等径孔隙模型,考虑微裂缝与孔隙之间的流体局部喷射流动,建立了一种动态等效介质模型,通过各向异性孔隙弹性(Anisotropic Poroelastic,APE)理论研究含有一组定向排列微裂隙的流体饱和岩石中波速度频散和衰减,由于流体流动考虑的是微观孔隙和裂隙尺度,预测的速度频散和衰减主要是在声波和超声频段,对地震频带段的衰减和频散的估计严重偏低。

Chapman[15]对孔隙弹性模型进行扩展,引入一套定向排列的中观尺度裂缝,基于流体喷射流动机制,提出了一种动态等效介质模型。该模型考虑了中观和微观两种尺度的流体流动,能够对地震频段地震波的频散和衰减给出合理的解释,且在低频、高频极限情况下,与各向异性Gassmann方程、Hudson孤立裂缝模型等价,表明其有效性。近年来一些学者基于此模型开展裂缝参数反演研究,反演结果与实际观测结果吻合良好[16]。Jakobson[17]和Chapman[18]采用T矩阵法将裂缝性孔隙介质中波场诱导的流体流动的地震波场尺度和波传播方向上压力梯度导致的全局流(达西流)以及在微观和细观尺度和不同于波传播方向上压力梯度导致的喷射流进行统一处理,提出了一种更为完善的等效介质理论模型。

Chapman裂缝性孔隙介质等效介质模型(图1)假设岩石的孔隙空间由各向同性的球形等径孔隙、定向或随机分布的椭球形微裂隙，以及定向排列的裂缝组成。其中微裂隙和孔隙的尺寸与颗粒的尺度相当,裂缝的尺寸要远大于颗粒的尺度但仍然小于地震波长尺度。Chapman模型考虑了两种不同尺度的裂缝,微裂隙之间、微裂隙与等径孔隙之间可相互连通,每条裂缝可与多个微裂隙或孔隙连通,但每个微裂隙和孔隙至多与一条裂缝连通。当裂缝性孔隙介质存在波诱导的流体压力梯度时,Chapman模型考虑两种尺度波场诱导的流体流动以及达到新的流体压力平衡时的状态,即,裂缝与微裂隙或球形等径孔隙之间的中观、细观尺度(大于孔隙尺寸,小于波场尺寸,典型的尺寸为数十厘米)达西流体流动状态,以及微裂缝与孔隙之间或不同方向微裂隙之间(微观颗粒尺度)喷射流体流动状态。

图1 Chapman[18]裂缝孔隙介质示意

Chapman模型的等效刚度张量表达式为:

C=C0-ΦpC1-εcC2-εfC3

(5)

式中：C0为岩石基质的各向同性弹性张量,可用固体颗粒的拉梅参数λ0,μ0表示；校正项中C1,C2和C3分别为来自孔隙、微裂隙和裂缝的附加贡献,它们都是拉梅常数、流体和裂缝性质、频率、与喷射流相关的弛豫时间等参数的函数；Φp,εc和εf分别为孔隙度、裂隙密度和裂缝密度。进出裂缝的流体对应低频特征频率ωf和大时间尺度松弛时间常数τf,取决于裂缝的尺寸;微观颗粒尺度的流体流动对应传统的喷射流特征频率(声波和超声波之间的频段)ωm和较小时间尺度的松弛时间常数τm。τf和τm之间的关系为:

(6)

式中：af是裂缝的半径；ag是颗粒的尺寸(孔隙和微裂隙尺度)。其物理意义是:随着裂缝半径的增加,裂缝表面积和体积的比值减小,达到流体压力平衡时将会有更多的流体通过单位表面积,因而需要更多的时间;与裂缝中流体流动相关的这一较大的流体压力弛豫时间τf导致地震频段内出现速度频散和衰减,也就是定向裂缝引起的各向异性具有频率相关性。

τm则由下式给出:

(7)

式中：cv为单个裂隙的体积；c1为裂隙与孔隙之间连接的数目；k为骨架的渗透率；η为流体的粘滞系数;σc=(πμr)/[2(1-υ)]为临界应力,或裂隙空间可压性的倒数,r为裂隙的横纵比,υ为泊松比；Kc=σc/kf,kf为流体的体积模量。

Chapman模型等效刚度张量取决于固体颗粒的拉梅系数λ0和μ0,岩石的密度ρ,孔隙度Φp，裂隙密度εc和裂缝密度εf,裂缝半径和裂隙半径的比r=af/ag,以及微裂隙尺度的喷射流弛豫时间τm。为克服低孔隙度适用性限制和拉梅系数计算弹性模量的误差,引入在某一频率f0下经过微裂隙和孔隙校正后的拉梅常数Λ和Υ,及校正的扰动函数Φc,p,则固体颗粒的拉梅系数λ0和μ0表示为:

(8)

则(5)式可进一步表示为:

(9)

其中，f是频率,张量的各个分量具体参数表达式(5个)在此略去,其中的参数最不容易确定的是弛豫时间τm,一般通过实验数据或根据经验给定。当球形孔隙的孔隙度远大于裂隙的孔隙度且研究频段低于微观喷射流的固有频率时,(9)式中与微裂隙有关的第3项可以略去,可使模型进一步简化。对一组垂直裂缝HTI介质5个独立等效粘弹性刚度参数C11,C13,C33，C44和C55的响应特征进行了分析[5],图2为各刚度参数的实部曲线;图3 为各刚度参数的虚部曲线。刚度参数分别是频率f，裂缝长度l和裂缝开度a的函数(由岩石物理模型给出)。观察到地震频段(1～100Hz)频散和衰减现象,特别是大尺度(0.2m)和开度(10-5m)的裂缝,也提示频变AVAZ地震反演裂缝,与裂缝几何尺寸关系密切,且不唯一。

Jakobsen[12]推导了等效渗透率张量公式,为裂缝参数(裂缝密度、裂缝长度,裂缝开度和方位裂缝方向等)的函数,表明等效渗透率对裂缝密度和和裂缝开度敏感,而几乎与裂缝长度无关。

图2 刚度参数的实部曲线(不同颜色曲线表示裂缝的长度和开度等几何参数不同)[5]

图3 刚度参数的虚部曲线(不同颜色曲线表示裂缝的长度和开度等几何参数不同)[5]

2 基于裂缝性孔隙介质等效模型的AVAZ正问题与分析

裂缝导致的岩石弹性性质的变化可以利用某些特别的地震属性进行检测,如振幅随方位的变化、横波双折射、波传播速度随方位的变化等。利用反射波振幅信息进行裂缝检测和裂缝参数的反演一直是裂缝性储层描述研究中的热点和难点。总结起来目前可以分为两类:一是从反射波数据中提取AVO属性,根据AVO属性随方位角度的变化,进行椭圆拟合,定性估计裂缝发育方位和发育强度;二是裂缝参数的定量反演,以裂缝介质等效模型描述裂缝性储层,根据相应的裂缝介质理论,建立反射波振幅随偏移距和方位角变化的关系,得到反射系数与裂缝参数的函数关系,从而反演出裂缝参数。上述理论均是基于弹性各向异性等效介质理论,裂缝介质中传播的地震波不发生速度频散和衰减,即静态等效介质理论。实践表明:裂缝性储层中传播的地震波由于波场诱导的流体在中观尺度裂缝和孔隙之间流动,而发生显著的频散和衰减,具有频率依赖的动态特征,需要考虑粘弹性各向异性等效介质理论,如Chapman等效介质模型,这种频率相关性与裂缝参数(裂缝密度、裂缝尺寸、裂缝开度、裂缝方位等)和流体性质参数(流体粘滞系数、体积模量等)密切相关。

基于动态等效介质理论,充分考虑频散和衰减,研究上覆各向同性均匀介质与裂缝性孔隙介质分界面处地震反射问题,进行频率依赖各向异性AVAZ分析,能够分析裂缝性孔隙介质储层参数变化的响应特征,对于裂缝检测、裂缝参数和流体性质定量反演具有重要意义。

基于Chapman模型,将频率依赖复值等效刚度张量引入HTI介质Ruger方程,就可以分析计算界面处PP波反射系数,这个反射系数显然是入射角θ,方位角φ(观测方位的方向与对称轴方向的差值),频率ω,以及裂缝模型参数矢量m的函数:

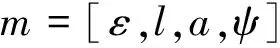
(10)

即裂缝模型参数,其中ε是裂缝的密度,l是裂缝长度,a为裂缝的横纵比,ψ为裂缝的走向。根据摄动法,Ruger方程PP波反射系数[22]如下:

(11)

图4 不同入射角PP波反射系数随方位角和频率的变化[22]

图5 不同入射角PP波反射系数随方位角和频率的变化[22]

利用不同入射角、方位角和分频的地震反射数据,可以构建非线性裂缝模型参数正问题:

(12)

函数G表达式基于Ruger近似方程与裂缝性孔隙介质岩石物理模型参数化关系式[5]。

3 裂缝性孔隙介质裂缝参数与各向异性渗透率反演

根据建立的正问题数学模型,利用频率依赖的地震AVAZ数据,可以反演裂缝性孔隙介质的裂缝密度、裂缝长度、裂缝孔径、裂缝方位等裂缝参数,进而可以确定等效的裂缝渗透率[5,12]。对应(12)式,反问题就是从不同地震频率、方位角和入射角相应的地震反射数据d,估算裂缝的模型参数m。实际上,由于地震数据存在不确定性,反问题的求解,需要采用统计模型处理观测误差,一般采用贝叶斯统计估计方法,即最大后验概率估计。假设模型参数满足高斯分布,使后验对数似然函数最大化,反问题的目标函数可表述为[5,12]:

(13)

式中：Cd为地震数据的协方差矩阵；mprior和Cm分别为裂缝参数的均值向量和协方差矩阵。采用蒙特卡洛方法实现贝叶斯随机反演。实际上,反问题求解的最大后验概率估计与吉洪诺夫正则化具有相同的解的形式。

Ali[5]给出了模型数据的数值算例。F-AVAZ数据基于动态等效岩石物理模型Ruger公式计算(公式(11)),作为观测数据。反演采用蒙特卡洛-马尔科夫模拟方法。将野外露头观测的裂缝长度作为先验约束信息,反演得到裂缝密度(ε)、长度(l)、开度(a)、方位(ψ)以及渗透率张量,结果如图6和图7所示；图中标注为模型给定的裂缝参数值和渗透率参数。

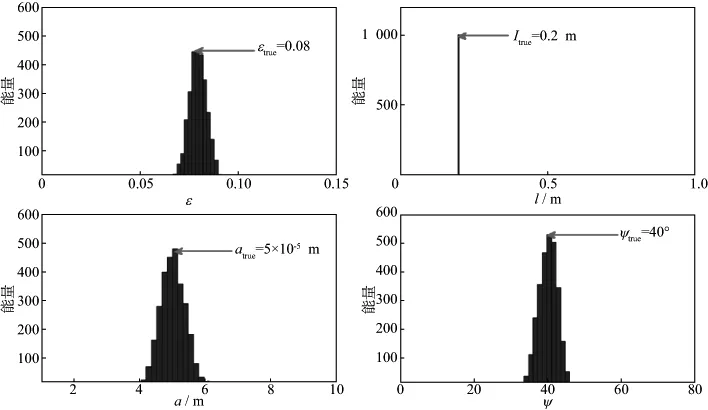
图6 模型数据裂缝参数先验约束反演结果[5]

图7 模型数据等效渗透率张量参数先验约束反演结果[5]

4 结束语

基于动态岩石物理等效介质理论的频变AVAZ反演方法,充分考虑地震波频散和衰减,为裂缝密度、长度、开度、方位等裂缝参数和渗透率参数等定量表征提供了非常有价值的思路。目前的研究进展,仅限于单个反射界面理论模型的计算数据,对于模拟地震数据和实际地震数据,利用该方法成功实现裂缝和渗透率定量表征还存在很多问题。特别是对于实际地震数据,需要考虑方位各向异性友好处理、保幅、分频、反演的实现策略等实际问题,尚未见到有效的技术流程和应用结果。需要进一步研究实际数据反问题的数学模型、反演方法和实现策略,地质和测井先验信息如何进行融合和约束则是关键。

[1] 曾联波,柯式镇,刘洋.低渗透油气储层裂缝预测研究方法[M].北京:石油工业出版社,2010:1-187 Zeng L B,Ke S Z,Liu Y.Fracture prediction methods for reservoirs with low porosity and permeability[M].Beijing:Oil Industry Press,2010:1-187

[2] Liu E,Martinez A.Seismic fracture characterization:concepts and practical applications [M].The Netherlands:EAGE,2012:1-280

[3] Chorpra S,Marfurt K J.Seismic attributes for prospect identification and reservoir characterization[M].Tulsa:Society of Exploration Geophysicists,2007:1-480

[4] Zhang J F,Zhang J J.Diffraction imaging using shot and opening-angle gathers:a prestack time migration approach[J].Geophysics,2014,79(2):S23-S33

[5] Ali A,Jakobsen M.Anisotropic permeability in fractured reservoirs from frequency-dependent seismic amplitude versus angle and azimuth data[J].Geophysical Prospecting,62(2):2014,293-314

[6] Hudson J A.Wave speeds and attenuation of elastic waves in material containing cracks[J].Geophysical Journal of Royal Astronomical Society,1981,64(1):133-150

[7] Schoenberg M,Sayers C.Seismic anisotropy of fractured rock[J].Geophysics 1995,60(1):204-211

[8] Thomsen L.Elastic anisotropy due to aligned cracks in porous rock[J].Geophysical Prospecting,1995,43(6):805-829

[9] Brown R,Korringa J.On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid[J].Geophysics,1975,40(4):608-616

[10] Gurevich B.Elastic properties of saturated porous rocks with aligned fractures[J].Journal of Applied Geophysics,2003,54(3-4):203-218

[11] Jakobsen M,Hudson J A,Johansen T A.T-matrix approach to shale acoustics[J].Geophysical Journal International,2003,154(2):533-558

[12] Jakobsen M,Liu E,Chapman M.Estimation of anisotropic permeability in fractured reservoirs[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007,99-103

[13] Hudson J A,Liu E,Crampin S.The mechanical properties of materials with interconnected cracks and pores[J].Geophysical Journal International,1996,124(1):105-112[14] Parra J O.Poroelastic model to relate seismic wave attenuation and dispersion to permeability anisotropy[J].Geophysics,2000,65(1):202-210

[15] Chapman M.Frequency dependent anisotropy due to meso-scale fractures in the presence of equantporosity[J].Geophysical Prospecting,2003,51(5):369-379

[16] Maultzsch S,Chapman M,Liu E,et al.Modelling frequency-dependent seismic anisotropy in fluid-saturated rock with aligned fractures,implication of fracture size estimation from anisotropic measurements[J].Geophysical Prospecting,2003,51(5):381-392

[17] Jakobsen M,Chapman M.Unified theory of global flow and squirt flow in cracked porous media[J].Geophysics,2009,74(2):WA65-WA76

[18] Chapman M.Modelling the effect of multiple sets of mesoscale fractures in porous rock on frequency-dependent anisotropy[J].Geophysics,2009,74(6):D97-D103

[19] Rüger A.Variation of P-wave reflectivity with offset and azimuth in anisotropic media[J].Geophysics,1998,63(3):935-947

[20] Tsvankin I.Reflection moveout and parameter estimation for horizontal transverse isotropy[J].Geophysics,1997,62(2):614-629

[21] 兰慧田.裂缝性孔隙介质波场模拟与频变AVO储层参数反演[D].吉林长春:吉林大学,2014 Lan H T.Seismic wave field modeling and frequency dependent AVO inversion of reservoir properties for fractured porous media[D].Jilin:Jilin University,2014

(编辑:朱文杰)

Progress on frequency-dependent AVAZ inversion for characterization of fractured porous media

Liu Xiwu,Dong Ning,Liu Yuwei

(SinopecExplorationandProductionResearchInstitute,Beijing100083,China)

It is still a challenge to use seismic method to characterize fractures quantitatively due to seismic data resolution scale.Based on dynamic effective medium modeling theory,Frequency-dependent amplitude versus angle and azimuth (F-AVAZ) inversion might give a prospective solution according to recent research progress.In this paper,a survey on F-AVAZ inversion method and its application for fracture parameters characterization is displayed.Firstly,the progress on the equivalent medium theory of fractured porous medium is introduced,and the static equivalent medium model and dynamic equivalent medium model of different fractured reservoirs are compared.On the basis of Chapman effective medium modeling theory,a forward model for quantitatively predicting fracture parameters and effective permeability tensors is investigated.Then a discussion on inversion methods and strategies are given with some numerical results.Finally,some challenges for application to real seismic data are presented and some possible research clues are given for further study.

multi-scale fractures,frequency-dependent seismic anisotropy,AVAZ,fracture parameters,quantitative inversion

2014-07-18;改回日期:2014-11-01。

刘喜武(1971—),男,副教授,研究方向为地震各向异性裂缝预测。

国家重点基础研究发展计划(973计划)(2014CB239104)和国家科技重大专项(2011ZX05066-002)联合资助。

P631

A

1000-1441(2015)02-0210-08

10.3969/j.issn.1000-1441.2015.02.013