基于杨氏模量、泊松比和各向异性梯度的裂缝介质AVAZ反演方法

杜炳毅,杨午阳,王恩利,张广智,高建虎

(1.中国石油勘探开发研究院西北分院,甘肃兰州730020;2.中国石油大学(华东)地球科学与技术学院,山东青岛266580)

基于杨氏模量、泊松比和各向异性梯度的裂缝介质AVAZ反演方法

杜炳毅1,杨午阳1,王恩利1,张广智2,高建虎1

(1.中国石油勘探开发研究院西北分院,甘肃兰州730020;2.中国石油大学(华东)地球科学与技术学院,山东青岛266580)

为了全面地描述裂缝介质的储层特征、流体性质和各向异性特征，提出了由宽方位叠前道集数据直接获取裂缝介质弹性参数和各向异性梯度参数的振幅随方位角变化(Amplitude Versus Azimuth,AVAZ)反演方法。首先推导了基于杨氏模量、泊松比和各向异性梯度的各向异性AVO方程,通过与Ruger近似进行对比,分析了该方程的近似精度。然后利用实际测井资料和二维逆掩断层模型建立了不同方位角的合成叠前角度道集,对未加噪声和信噪比为3的宽方位叠前角度道集进行了AVAZ反演方法测试,结果表明,未加噪声和信噪比为3的合成宽方位叠前道集均能反演得到符合地震反演精度的杨氏模量(E),泊松比(σ)和各向异性梯度(Γ),噪声对杨氏模量的反演影响较小,不含噪声时泊松比和各向异性梯度的反演精度更高,与真实值吻合程度较高。

杨氏模量;泊松比;各向异性梯度;裂缝介质;AVAZ反演

Thomsen[1]提出了弱各向异性介质理论,引入了弱各向异性参数,为各向异性的研究奠定了基础;Ruger[2]对HTI介质的反射与透射特征进行了详细的研究,推导了纵波反射系数近似公式,并分析了方位各向异性与入射角和方位角的关系;Bakulin等[3]和Sayers等[4]利用带有线性滑动边界条件的有限平行裂缝和硬币型裂缝理论来估计各向异性参数与裂缝结构之间的关系,进而估测裂缝的发育方向和裂缝密度,利用各向异性差值判断裂缝的含油气性。AVAZ反演中弹性参数和各向异性参数的反演具有很多的不确定性,不同的学者对此进行了相关的研究。Subhashis等[5]利用纵波和转换波随入射角和方位角的变化特征进行AVAZ反演，得到稳健的各向异性参数估计值;Downtown等[6-7]运用贝叶斯理论估计HTI介质AVAZ反演的弹性参数预测值的不确定性,提出了同步弹性参数反演,加入岩石物理模型的约束,克服了AVAZ反演的固有缺陷,从而定量地解释AVAZ反演的稳定性。

为了更好地识别裂缝储层特征,孔丽云等[8]深入分析了裂缝孔隙、裂缝弱度、裂缝渗透率等参数对双孔隙裂缝介质地震各向异性的影响。P波反射振幅与弹性参数之间的关系是裂缝性储层反演研究的主要问题之一,刘军迎等[9]认为裂缝储层的反射振幅随着观测方位的变化而变化,表现出明显的方位各向异性特征,可以应用该特征来预测碳酸盐岩储层中的裂缝密度及发育方向。张广智等[10]研究了裂缝弹性参数的各向异性AVO反演方法,准确地得到了反映储层特征的纵波阻抗、横波阻抗以及各向异性梯度。陈怀震等[11-12]研究了纵波动力学特征与裂缝流体因子、缝隙流体因子、裂缝密度、入射角和方位角等因素之间的关系特征,通过合成的模型数据对该方法的适用性进行了详细的分析。宗兆云等[13]分析了纵波模量、横波模量、杨氏模量和泊松比对储层反射特征的影响,提出了利用叠前AVO反演方法直接估算纵波模量、横波模量、杨氏模量和泊松比的算法,避免了间接求取带来的误差累积,为裂缝型储层的识别提供了更加可靠的理论依据;宗兆云等[14]通过建立纵横波模量、密度以及各向异性差值与纵波反射系数之间的关系,进一步估测地层的地应力,这对页岩气储层的评价是非常有利的。裂缝储层的弹性阻抗也表现为强方位各向异性特征,通过方位各向异性弹性阻抗反演可以获取表征裂缝性质的弹性参数和各向异性参数[15-16]。

杨氏模量是表示岩石抗压缩能力的物理量,表征了储层的岩性特性;泊松比是横向应变与纵向应变的比值绝对值,与储层流体性质有关。为了全面地描述裂缝介质的储层特征、流体性质和各向异性特征,本文在上述研究的基础上,建立了裂缝介质的纵波反射系数与杨氏模量、泊松比和各向异性梯度之间的关系,利用模型数据对新的AVAZ反演算法进行测试,取得了较好的应用效果。

1 方法原理

裂缝介质的各向异性特征可以由Thomsen提出的弱各向异性参数ε(v),δ(v),γ来表征,它们与弹性矩阵之间的关系为[1]：

(1)

Ruger研究了各向异性半空间界面的地震波反射特征,推导了纵波反射系数随入射角、方位角变化的关系式[2],如(2)式所示：

(2)

按照扰动理论,分为背景场和扰动场,可以将纵波的AVO近似方程表示为：

(3)

(4)

(5)

宗兆云推导了纵波近似反射系数与杨氏模量(E),泊松比(σ)和密度反射系数之间的变化关系式[14]：

(6)

(7)

式中:C是一个常数;g为纵波速度的幂指数。

对其求一阶偏导,求出密度反射系数与纵波速度反射系数的关系：

(8)

最后,可以求得密度反射系数与杨氏模量反射系数、泊松比反射系数的函数表示式：

(9)

将其代入到(6)式中,进一步得到：

(10)

Chen等[11]指出,在入射角小于30°的情况下,可以令sin2θtan2θ≈0,(5)式可以进一步简化为：

(11)

Ruger定义各向异性梯度Γ为：

(12)

最终,可以得到基于杨氏模量、泊松比和各向异性梯度的P波AVAZ近似方程：

(13)

在上述推导的基础上,选取两层的裂缝介质模型,相关参数如表1所示,对新推导的纵波AVAZ近似方程进行精度分析。由Ruger近似得到曲线和新推导公式的近似曲线对比结果(图1),对比发现,在入射角较大的情况下,新推导方程的近似精度与Ruger近似吻合程度较高,因此,利用该方程进行裂缝介质AVAZ反演可以提高裂缝预测的精度。

表1 裂缝模型参数

在不同方位角和入射角的情况下,可以将(13)式表示为矩阵的形式：

(14)

图1 新推导方程与Ruger近似方程的精度对比

令：

(15)

(16)

(17)

(14)式可以表示为：

d=Gm

(18)

利用最小二乘算法求取出模型参数的最佳估算值：

(19)

2 实际模型测试

2.1 实际工区测井资料合成叠前角度道集的AVAZ反演方法测试

为了验证反演算法的有效性,本文选取某实际工区的纵波速度、横波速度和各向异性参数等测井曲线(图2),利用新推导的公式求取不同入射角(0～30°)和方位角(0,30°,60°,90°)的P波AVO反射系数,并且与40Hz的雷克子波褶积得到不同方位角的叠前合成角度道集,对其添加信噪比为3的随机噪声。分别对不含噪声和信噪比为3的合成数据进行算法测试。图3是密度和纵波速度的幂指数拟合,拟合点基本分布在公式(7)所表示的曲线附近,说明密度和纵波速度之间满足关系式(7)。

图4是不含噪声时合成的不同方位角(0,30°,60°,90°)的叠前角度道集;图5是未加噪声合成数据经过基于杨氏模量、泊松比和各向异性梯度反演得到的反演结果与真实结果的对比;图6是信噪比为3时合成的不同方位角(0,30°,60°,90°)的叠前角度道集;图7是信噪比为3的合成数据经过基于杨氏模量、泊松比和各向异性梯度反演得到的反演结果与真实结果的对比。对比图7与图5可以看出，噪声对杨氏模量的反演影响较小；不含噪声时泊松比和各向异性梯度的反演精度更高，与真实值吻合程度较高。

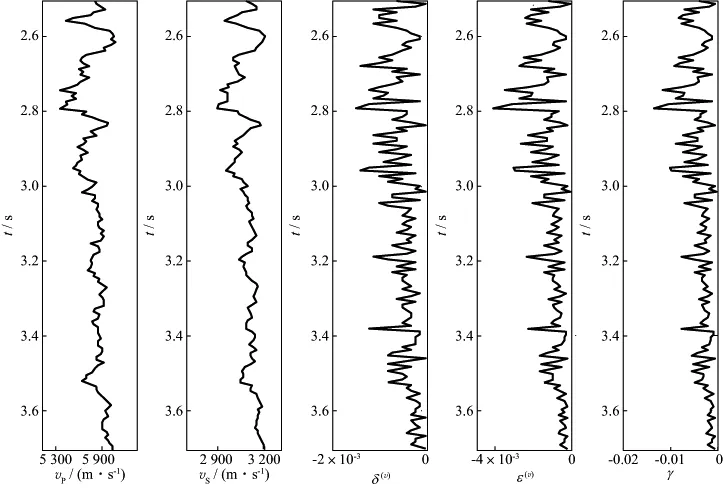
图2 某实际工区的测井曲线

图3 密度和纵波速度的幂指数拟合

图4 不加噪声时合成的不同方位角的叠前角度道集

图5 未加噪声合成数据的杨氏模量、泊松比和各向异性梯度反演值(红色)与真实值(蓝色)对比

图6 信噪比为3时合成的不同方位角的叠前角度道集

图7 信噪比为3合成数据的杨氏模量、泊松比和各向异性梯度反演值(红色)与真实值(蓝色)对比

2.2 二维逆掩断层模型测试

再应用上述AVAZ反演方法对二维逆掩断层模型进行算法测试,进一步验证该算法的合理性。图8给出了二维逆掩断层的原始模型剖面,分别是杨氏模量剖面(图8a)、泊松比剖面(图8b)和各向异性梯度剖面(图8c)。通过正演模拟得到二维逆掩断层模型不同方位角(0,30°,60°,90°)的合成地震角度道集,并且加入信噪比为3的随机噪声。利用含噪声合成地震记录直接通过AVAZ反演获取二维逆掩断层模型的杨氏模量、泊松比和各向异性梯度,反演结果如图9所示。由图9可以看到，杨氏模量、泊松比和各向异性梯度均能准确反映该模型的构造特征,清晰地展示了地层界面,具有很强的横向连续性。测试结果进一步验证了新的P波AVAZ近似公式的正确性和反演算法的有效性。

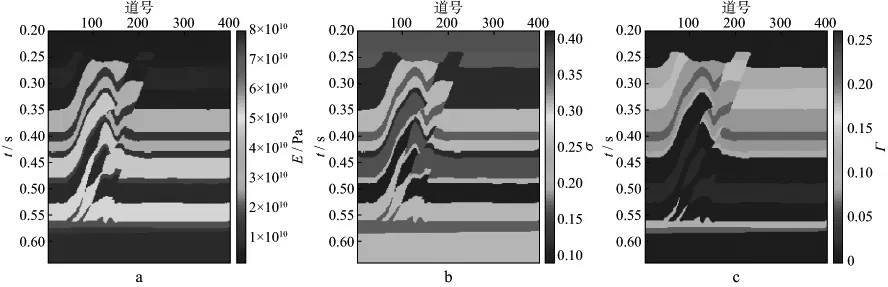
图8 二维逆掩断层模型的杨氏模量(a)、泊松比(b)和各向异性梯度(c)的原始剖面

图9 二维逆掩断层模型合成道集(信噪比为3)的杨氏模量(a)、泊松比(b)和各向异性梯度(c)的反演结果

3 结论与认识

本文推导了基于杨氏模量、泊松比和各向异性梯度的方位各向异性AVO方程,提出了一种AVAZ反演算法；选用某实际工区的测井数据和二维逆掩断层模型合成不同方位角的叠前角度道集测试了该AVAZ反演算法,为裂缝介质参数反演的发展提供了新的思路。通过以上研究工作可以得出以下结论与认识。

1) 对新推导的方位各向异性AVO方程进行精度分析,通过与Ruger近似方程对比,可以看出新推导的方程能够满足裂缝介质AVAZ反演的精度要求。

2) 选择实际井资料模型和二维逆掩断层模型,合成不同方位角的叠前角度道集对AVAZ反演算法进行测试,结果表明,杨氏模量、泊松比和各向异性梯度的反演结果与真实值吻合程度较高,能够反演裂缝储层的构造特征和岩性特征等信息。

3) 值得指出的是，裂缝介质中流体的识别是裂缝介质研究的主要目的之一,因此，下一步需要对基于上述AVAZ反演结果的裂缝流体识别进行深入的研究。

[1] Thomsen L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954-1966

[2] Ruger A.Reflection coefficients and azimuthal AVO analysis in anisotropic media[D].Colorado:Colorado School of Mines Golden,1996

[3] Bakulin A,Grechka V,Tsvankin I.Estimation of fracture parameters from reflection seismic data—part I:HTI model due to a single fracture set[J].Geophysics,2000,65(6):1788-1802

[4] Sayers C M,Simon D.Azimuth-dependent AVO in reservoirs containing non-orthogonal fracture sets[J].Geophysical Prospecting,2001,49(1):100-106

[5] Subhashis M,Diana G.Azimuthal reflectivity and quantitative evaluation of anisotropic parameters from seismic data a feasibility study[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,182-185

[6] Downton J,Gray D.AVAZ parameter uncertainty estimation[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006,234-238

[7] Downton J,Roure R.Azimuthal simultaneous elastic inversion for fracture detection[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010,263-267

[8] 孔丽云,王一博,杨慧珠.裂缝诱导HTI双孔隙介质中的裂缝参数分析[J].地球物理学报,2012,55(1):189-196 Kong L Y,Wang Y B,Yang H Z.Fracture parameters analyses in fracture -induced HTI double-porosity medium[J].Chinese Journal of Geophysics,2012,55(1):189-196

[9] 刘军迎,雍学善,杨午阳,等.基于叠前方位振幅的大港—埕海地区奥陶系风化壳裂缝储层的叠前预测[J].地球物理学进展,2012,27(4):1588-1597 Liu J Y,Yong X S,Yang W Y,et al.Pre-stack fracture reservoir bed estimation of Ordovician weather layer of Dagang-Chenghai area based on azimuthal pre-stack seismic amplitude[J].Progress in Geophysics,2012,27(4):1588-1597

[10] 张广智,陈怀震,印兴耀,等.基于各向异性AVO的裂缝弹性参数叠前反演方法[J].吉林大学学报(地球科学版),2012,42(3):845-871 Zhang G Z,Chen H Z,Yin X Y,et al.Method of fracture elastic parameter inversion based on anisotropy AVO[J].Journal of Jilin University(Earth Science Edition),2012,42(3):845-871

[11] Chen H Z,Zhang G,Yin X.AVAZ inversion for elastic parameter and fracture fluid factor[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012,1-5

[12] 陈怀震,印兴耀,高成国,等.基于各向异性岩石物理的缝隙流体因子AVAZ反演[J].地球物理学报,2014,57(3):968-978 Chen H Z,Yin X Y,Gao C G,et al.AVAZ inversion for fluid factor based on fracture anisotropic rock physics theory[J].Chinese Journal of Geophysics,2014,57(3):968-978

[13] 宗兆云,印兴耀,吴国忱.基于叠前地震纵横波模量直接反演的流体检测方法[J].地球物理学报,2011,55(1):284-292 Zong Z Y,Yin X Y,Wu G C.Reflection coefficient equation and pre-stack inversion with Young’s modulus and poisson ratio[J].Chinese Journal of Geophysics,2011,55(1):284-292

[14] 宗兆云,印兴耀,张峰,等.杨氏模量和泊松比反射系数近似方程及叠前地震反演[J].地球物理学报,2012,55(11):3786-3794 Zong Z Y,Yin X Y,Zhang F,et al.Reflection coefficient equation and pre-stack seismic inversion with Young’s modulus and poisson ratio[J].Chinese Journal of Geophysics,2012,55(11):3786-3794

[15] Zong Y Z,Yin X Y,Wu G C.AVAZ inversion and stress evaluation in heterogeneous medium[J].Expanded Abstracts of 83rdAnnual Internat SEG Mtg,2013,428-431

[16] 陈怀震,印兴耀,杜炳毅,等.裂缝型碳酸盐岩储层方位各向异性弹性阻抗反演[J].地球物理学进展,2013,28(6):3073-3079 Chen H Z,Yin X Y,Du B Y,et al.Azimuthal anisotropic elastic impedance inversion in fractured layered carbonate rock reservoir[J].Progress in Geophysics,2013,28(6):3073-3079

[17] 窦喜英,韩立国,刘春成,等.裂缝型HTI介质中的弹性阻抗[J].吉林大学学报地球科学版,2012,42(4):1192-1197 Dou X Y,Han L G,Liu C C,et al.Elastic impedance in fracture medai[J].Journal of Jilin University(Earth Science Edition),2012,42(4):1192-1197

(编辑：陈 杰)

AVAZ inversion based on Young’s modulus,Poisson’s ratio and anisotropy gradient in fractured media

Du Bingyi1,Yang Wuyang1,Wang Enli1,Zhang Guangzhi2,Gao Jianhu1

(1.NorthwestBranch,ResearchInstituteofPetroleumExploration&Development,Petrochina,Lanzhou730020,China; 2.SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China)

In order to fully describe the reserroir characteristics,fluid properties and anisotropy in fractured media,we proposed an algorithm of Amplitude Versus Azimuth (AVAZ) inversion to obtain elastic parameters and anisotropy parameters of fractured media by using wide azimuthally pre-stack seismic data.Firstly,a new P-wave azimuth AVO approximate equation based on Young’s modulus,Poisson’s ratio and anisotropy gradient is deduced.The precision of this new equation was analyzed and compared with Ruger’s equation.Then,we utilized actual log data and 2D overthrust model to generate synthetic pre-stack angle gathers of wide-azimuth data.The algorithm is tested through the wide-azimuth synthetic angle gathers without noise and with random noise (SNR=3) respectively.The result shows that the inverted Young’s modulus,Poisson’s ratio and anisotropy gradient without noise is estimated exactly and agreed with the original data.Meanwhile,the inversion result of the data with random noise (SNR=3) is stable and can meet the demand of seismic inversion.Noise causes less influence on the inversion of Young’s modulus,the invesion accuracy of Poisson’s ratio and anisotropy gradient is higher without noise which is well coinciding with the actual data.

Young’s modulus,Poisson’s ratio,anisotropy gradient,fractured media

2014-09-13;改回日期：2014-12-19。

杜炳毅(1985—),男,硕士,主要从事叠前地震反演和储层流体识别方面的研究。

国家科技重大专项(2011ZX05019-008-005)资助。

P631

A

1000-1441(2015)02-0218-08

10.3969/j.issn.1000-1441.2015.02.014