非局部平均滤波噪声压制方法及其在VSP资料逆时偏移中的应用

王维红，郭雪豹，石 颖

(东北石油大学地球科学学院，黑龙江大庆163318)

非局部平均滤波噪声压制方法及其在VSP资料逆时偏移中的应用

王维红，郭雪豹，石 颖

(东北石油大学地球科学学院，黑龙江大庆163318)

基于双程波的逆时偏移会产生低频成像噪声，在成像后运用拉普拉斯滤波法可以取得较好的压噪效果，但是，该方法严重依赖于角度参数，使得滤波后的成像剖面上常常存在同相轴不光滑和噪声压制不完全的情况。基于叠后地震资料同相轴结构的特点，为进一步提高逆时偏移叠加数据的信噪比，引入了非局部平均滤波法，针对拉普拉斯滤波后的成像数据进行进一步的压噪处理。非局部平均滤波法将输入的地震数据分解为不含噪声的地震数据和噪声数据两部分，利用不同成像点与其它成像点间的相似系数，实现滤波处理。二维复杂模型VSP正演模拟数据逆时偏移结果的试算表明，应用非局部平均滤波后的剖面信噪比得到进一步提高，同相轴的连续性明显增强。实际VSP资料逆时偏移低频噪声压制试处理也表明非局部平均滤波方法具有计算精度高、算法稳定性好和易于实现的特点。

非局部平均;噪声压制;逆时偏移;垂直地震剖面;拉普拉斯滤波

随着计算机硬件技术的发展，近年来基于双程波方程的逆时偏移方法得到了快速发展和应用[1-2]。除地面地震资料的逆时偏移成像外，井中地震资料，特别是VSP资料的逆时偏移技术也得到一定程度的发展，为井中地震高精度成像奠定了基础[3-5]。在逆时偏移方法研究中，一般来说选择互相关成像条件进行成像计算，互相关成像条件可为成像提供准确的动力学特性[6]，而且实现方法简单，但是该成像条件会使逆时偏移结果产生大量强振幅的低频噪声[7]。对于低频噪声的压制，主要有波场延拓噪声压制方法、应用有效成像条件的噪声压制方法和成像后滤波的噪声压制方法等。

Baysal等[8]提出了无反射波动方程来压制低频噪声，但由于该方法与叠前逆时偏移噪声的产生机理有本质上的区别，所以不适用于叠前处理;Leowenthal等[9]提出通过平滑速度模型来减少反射波。对入射角较大的情况，上述两种方法依旧会产生反射，因此噪声压制效果不很明显。Fletcher等[10]提出了双程无反射方程来压制低频噪声，该方法在方程中引入密度项，使得波阻抗为常数，虽然解决了逆向散射的问题，但只在垂直入射时应用效果好，随着入射角度的增大，反射波的能量逐渐增强，该方法的实用性就变得很差。应用有效成像条件压制噪声的实质就是对互相关成像条件进行改进，以达到噪声压制的效果。Kaelin等[11]通过实验得出结论，可以借助检波照明来改善成像条件，分别试验了波场分解成像条件、归一化成像条件、坡印廷矢量成像条件和立体成像条件，这些方法存在的共同缺陷是对噪声不能有效完全压制，使得地震成像数据体的解释和应用受到很大影响。成像后滤波法中最简单的是高通滤波，但这种方法对噪声压制不彻底，并且会破坏有效波场的低频信息[12]。Guitton等[13]提出在波数域对噪声进行压制，分别对微分滤波、拉普拉斯滤波、最小平方滤波进行了试验。Zhang等[14]指出在叠加偏移的角道集中，通过对大反射角的噪声抑制来消除噪声是逆时偏移低频噪声压制的有效方法，并提出在成像过程中引入拉普拉斯算子进行噪声压制，运用拉普拉斯滤波，相当于给角道集加权。拉普拉斯滤波法在逆时偏移的研究中的应用较为广泛且有效。

非局部平均(Non-local Means，NLM)滤波最早由Buades等[15]提出的，该算法利用成像点窗口与临近窗口间的相似性来加强构造信息，从而实现随机噪声的压制。非局部平均方法最初应用于图像处理，由于非局部平均算法对每一个成像点降噪时需要计算全部成像点的相似系数，因此具有较大的计算量[16]。许多学者为减少计算时间做了不同的研究，Sheng等[17]将算法在GPU上运行，取得了较好的效果。Mahmoudi等[18]、Brox等[19]为减少每个成像点的计算时间，将求取相似系数限制在成像点为中心的一个范围内。这些改进算法较原本的算法节省了大量的计算时间。目前非局部平均算法已成功应用于医学数据、雷达数据、音频数据、显微成像等领域[20-23]。Bonar等[24]将该方法引入地震资料处理中，进行了地震资料随机噪声压制处理。对应用拉普拉斯滤波压制低频噪声后的逆时偏移地震数据体，再应用非局部平均滤波方法进行噪声的压制处理，可进一步提高地震数据的信噪比，为地震资料的精细解释和有效应用提供高质量的基础数据。

1 非局部平均算法原理

非局部平均滤波依据图像结构或地震数据同相轴结构的特点，在不同像素点通过对图像结构增强，实现噪声压制的目的[24]。其基本原理如下。

对一含有噪声的成像结果I，可应用下式表示：

(1)

式中：U为不含噪声的成像数据;N表示噪声。

(2)

式中：w(m,k)为m和k之间成像值的相似性，其满足0≤w(m,k)≤1且∑kw(m,k)=1。其中，每个m都存在与k相关的相似系数。为定量表示相似性，定义Nm为以m为中心的窗口，为计算Nm和Nk之间的相似性，采用高斯加权欧几里得距离表示：

(3)

(4)

式中：x0，y0为高斯函数中心，其中坐标x，y与上式中的l项对应，u为偏离参数。

Nm和Nk之间的相似系数可以表示为：

(5)

图1说明了成像点间相似系数计算原理，图中虚线框内列出了4个图像框。计算以框1中圆点为中心的窗口与以周围点为中心的窗口之间的相似系数，如计算框1中心点与框2中心点之间的相似系数。首先确定窗口大小，即以点为中心的框所包括的数据大小;然后对框1与框2之间的数据计算高斯欧几里得距离;最后算出两框中心点之间的相似系数。Budas等[15]给出的非局部平均滤波是对全局计算相似系数，也就是说对于图1，需要计算框1中心点与成像体内其余所有点之间的相似系数，这样会产生较大的计算量。所以，仅用以框1圆点为中心的虚线边框内的所有点来计算相似系数，可大大减小计算量，提高计算效率。

图1中仅就框1和框2内点的顺序计算相似系数可能较为片面，实际上为使滤波效果更好，应充分考虑输入数据的不同对称性。图2给出了以成像点为中心的窗口的选取，在计算成像点之间相似系数的时候，如计算框1中心点和框2中心点相似系数时，对框2做如图2所示的翻转，并分别与框1求取相似系数，取其中最大值作为该点的相似系数，可使滤波效果更好。

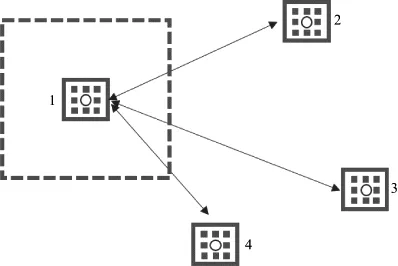
图1 成像点间相似系数计算原理

图2 成像点窗口对称性示意

2 VSP资料逆时偏移中的低频噪声

众所周知，单程波偏移结果没有强能量噪声或者说不存在成像噪声，是由于单程波偏移方法限制了波场的传播方向，炮点正向延拓的波场遇到反射面时只考虑向下传播，因此成像只发生在炮点与检波点波场传播方向相反的位置。

与单程波偏移方法不同，基于双程波的逆时偏移会产生低频噪声。根据Claerbout[6]提出的时间一致性成像原理及互相关成像条件，成像点位于震源波场外推与接收波场外推时间相一致之处。对于双程延拓的逆时偏移来说，由于不限制传播方向，在射线路径上的每个点都满足ts=tr，也就是说在整个射线传播的路径上，成像条件都是满足的，因此会在整条射线传播路径上成像。如果直接利用公式作为成像条件，会产生非常强的低频噪声，特别是在浅层强反射界面上方，产生的低频噪声足以将浅层构造完全淹没。图3给出了叠前逆时偏移低频噪声的产生机制[7]。

逆时偏移低频噪声压制应用最为广泛的方法是拉普拉斯滤波法。Zhang等[14]采用对大反射角的噪声抑制法来压制低频噪声，指出拉普拉斯滤波相当于给角道集加权。拉普拉斯算子噪声压制方法简单易操作，一般将其写成二阶差分的形式用于逆时偏移成像后滤波，对噪声压制效果较为明显。

二维拉普拉斯算子可表示为：

(6)

在波数域可以表示为

(7)

其中，kx和kz分别为x和z方向的波数。kI为成像域中的波数矢量kI=kr-ks,其中ks和kr分别为震源处波场和检波点处波场的波数矢量。

图3 逆时偏移低频噪声产生机制(据刘红伟等[7])

由余弦定理得到：

(8)

由(7)式和(8)式可得:

(9)

从(9)式可以看出，采用拉普拉斯算子进行噪声压制相当于给逆时偏移成像结果乘以一个权系数，这个系数与入射角θ有关，θ越大，权系数越小;θ越小，权系数越大。当θ=90°时，噪声可完全消除。为满足保幅的处理要求，在将拉普拉斯算子用于逆时偏移数据体的噪声压制时，(9)式中的速度v可以直接从速度模型提取，频率ω需要在成像前完成补偿。

为试验VSP逆时偏移低频噪声压制效果，设计了如图4所示的复杂二维理论模型，纵向、横向网格点数分别为800和600，网格间距均为5m。采用地面放炮井中接收的观测方式。震源从地表左端100m开始，向右每隔100m模拟一炮VSP记录，共39炮。设计两口VSP井接收，分别放于模型的最左端和最右端，分别记为1号井(左端)和2号井(右端)，井中自地表开始部署600个检波器，检波器的间隔为5m。震源为主频30Hz的Ricker子波，时间采样间隔(计算步长)为0.5ms，采样点数为5000。图5给出的是左端1号井的正演炮记录，图5a为第1炮的炮记录(震源位于模型地表100m处)，图5b为第20炮的记录，也就是震源位于模型地表中间位置(偏移距2000m)的正演单炮记录。可以看出，图5a的上行波和下行波同相轴很清晰，易于识别;图5b震源远离井口，波场特征变得比较复杂，同相轴很难识别，同时也表现出了复杂构造模型的特点。

图4 双井变偏VSP的井间二维速度模型

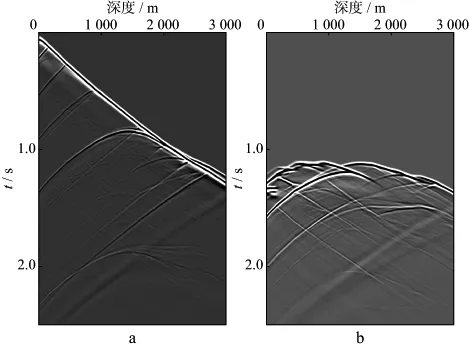
图5 正演模拟的左端1号井VSP单炮记录

基于二维声波方程，采用优化十二阶差分，对以上模拟VSP数据进行了逆时偏移计算。图6a为变偏VSP逆时偏移互相关成像的结果，具有明显的低频噪声；图6b为经拉普拉斯滤波后的成像数据，可以看出低频噪声得到较好的压制，表明拉普拉斯滤波方法可以取得不错的低频噪声压制效果。但从图6b中也可以看出，在高速地质体的两侧，同相轴的光滑性和连续性都不令人满意，对后续地质构造解释造成较大困难。

图6 模拟VSP数据逆时偏移结果(a)和经拉普拉斯滤波法压制低频噪声后的结果(b)

3 非局部平均滤波法噪声压制

基于非局部平均滤波基本理论，编程实现了非局部平均滤波噪声压制方法。对图6给出的经拉普拉斯滤波后的成像数据体进行非局部平均滤波处理。在实际处理时，所需输入的速度文件可直接从逆时偏移的速度模型读出，理论上讲，输入的模型越精确，滤波后噪声压制效果越好。为检验方法的实用性，将图4所示的二维速度模型进行平滑，平滑之后的速度模型如图7所示，用该模型作为非局部平均滤波求取相似系数的输入速度文件。将以上模拟VSP数据的逆时偏移结果(图6a)进行拉普拉斯滤波后(图6b)，再进行非局部平均滤波获得的结果如图8所示。对比图6b，可以看出图8中噪声明显减少，同相轴的光滑性和连续性均得到增强。为更清晰地对比两种方法的噪声压制效果，进行局部放大显示。图9a是图6b的局部放大图，图9b是图8对应位置的局部放大，对比可知，经非局部平均滤波后，成像数据体的噪声得到明显压制，地震资料的信噪比得到有效提高，为后续地震资料的精细解释和应用提供了高质量的基础数据。

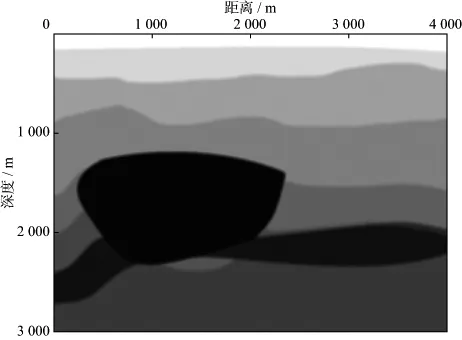
图7 图4所示速度模型平滑后的结果

图8 图6b剖面再经非局部平均滤波后的结果

图9 图6b剖面(a)和图8剖面(b)去噪效果的局部放大显示

为进一步测试非局部平均滤波方法的实际应用效果，对某地区实际变偏VSP数据进行了试处理。该数据共411炮，40级检波器接收。速度模型横向和纵向网格间距均为10m，时间步长为0.5ms。图10给出了实际VSP数据逆时偏移结果的低频噪声压制效果对比，图10a为逆时偏移结果经拉普拉斯滤波后的成像剖面，图10b为进一步进行非局部平均滤波后的成像剖面。对比图10a与图10b可以看出，在没有改变同相轴形态的情况下，应用非局部平均滤波后偏移噪声进一步得到压制，剖面整体信噪比得到了有效提高。

需要说明的是，非局部平均滤波方法是对叠后的数据体进行滤波操作，因此其计算时间与叠前偏移的炮数无关，仅与偏移数据体的网格大小和非局部平均滤波所采用的计算参数有关，以图10b所给出的实际数据为例，非局部平均滤波计算时间为105s，可见该滤波方法的计算效率很高，具有很强的实用性。

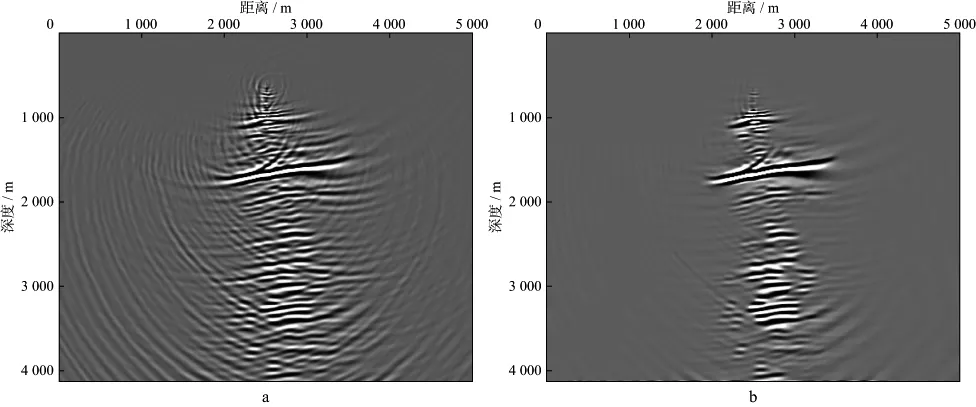
图10 实际变偏VSP数据逆时偏移结果的低频噪声压制效果对比

4 结论与建议

1) 基于双程波动方程的逆时偏移是当前复杂构造地震成像中精度高、应用广泛的方法，但是该方法会产生能量很强的低频噪声。在当前的低频噪声压制方法中，拉普拉斯滤波法应用效果较好。

2) 非局部平均滤波噪声压制方法应用地震数据中不同成像点与其它成像点之间的相似性进行噪声压制，对逆时偏移后的成像数据体几乎没有任何假设，具有较强的适应性。另外，该方法在叠后数据体上进行噪声压制处理，计算效率较高，易于实现，可根据成像数据体的情况选择不同的计算参数。

3) 在应用拉普拉斯滤波对理论模拟的复杂构造变偏VSP数据逆时偏移成像结果进行低频噪声压制后，再应用非局部平均滤波噪声压制方法可使数据的信噪比得到进一步提高，同相轴的连续性得到增强。实际数据试算结果表明该方法可有效应用于VSP地震资料逆时偏移中。当然，该方法也可以应用于地面地震资料逆时偏移成果数据的低频噪声压制，具有广泛的适用性。

[1] Zhang Y,Duan L,Xie Y. A stable and practical implementation of least-squares reverse time migration[J]. Geophysics,2015,80(1):23-31

[2] 刘文卿,王西文,刘洪，等. 盐下构造速度建模与逆时偏移成像研究及应用[J].地球物理学报,2013,56(2):616-625 Liu W Q,Wang X W,Liu H,et al. Application of velocity modeling and reverse time migration to subsalt structure[J]. Chinese Journal of Geophysics (in Chinese),2013,56(2):612-625

[3] 孙赞东. 三维三分量VSP方法原理及应用[M]. 北京:石油工业出版社,2011:1-4 Sun Z D. The principle and application of 3D three-component VSP method[M]. Beijing:Petroleum industry press,2011:1-4

[4] 朱金明,严俊华. VSP逆时偏移处理[J]. 石油地球物理勘探,1991,26(5):564-570 Zhu J M,Yan J H. VSP reverse-time migration[J]. Oil Geophysical Prospecting,1991,26(5):564-570

[5] 朱金明,董敏煜,李承楚. VSP的双程无反射波动方程逆时偏移[J]. 石油地球物理勘探,1989,24(3):256-270 Zhu J M,Dong M Y,Li C C. VSP reverse-time migration using two-way nonreflection wave equation[J]. Oil Geophysical Prospecting,1989,24(3):256-270

[6] Claerbout J F. Toward a unified theory of reflector mapping[J]. Geophysics,1971,36(3):467-481

[7] 刘红伟,刘洪,邹振,等. 地震叠前逆时偏移中的去噪与存储[J]. 地球物理学报,2010,53(9):2171-2180 Liu H W,Liu H,Zou Z,et al. The problems of denoise and storage in seismic reverse time migration[J]. Chinese Journal of Geophysics (in Chinese),2010,53(9):2171-2180

[8] Baysal E,Kosloff D,Sherwood J. A two-way nonreflecting wave equation[J]. Geophysics,1984,49(2):132-141

[9] Loewenthal D,Stoffa P A,Faria E L. Suppressing the unwanted reflections of the full wave equation[J]. Geophysics,1987,52(7):1007-1012

[10] Fletcher R F,Fowler,Kitchenside P. Suppressing artifacts in prestack reverse-time migration[J]. Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005,2049-2051

[11] Kaelin B,Guitton A. Imaging condition for reverse time migration[J]. Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006,2594-2598

[12] Mulder W,Plessix R. One-way and two-way wave-equation migration[J]. Expanded Abstracts of 73rdAnnual Internat SEG Mtg,2003,881-884

[13] Antoine Guitton,Bruno Kaelin,Biondo Biond. Least-square attenuation of reverse time migration artifacts[J]. Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006,2348-2352

[14] Zhang Y,Sun J. Practical issues of reverse time migration:true amplitude gathers,noise removal and harmonic-source encoding[J]. First Break,2009,26(1):29-35

[15] Buades A,Coll B,Morel J M. A review of image denoising algorithms,with a new one[J]. Multiscale Modeling and Simulation,2005(4):490-530

[16] Buades A,Coll B,Morel J M. Image denoising methods:a new nonlocal principle[J].SIAM Review,2010,52(1):113-147

[17] Sheng B,Li P,Sun H. Image-based material restyling with fast non-local means filtering[J]. Proceedings of the 2009 Fifth International Conference on Image and Graphics,2009,841-846

[18] Mahmoudi M,Sapiro G. Fast image and video denoising via nonlocal means of similar neighborhoods[J]. IEEE Signal Processing Letters,2005,12,839-842

[19] Brox T,Kleinschmidt O,Cremers D. Efficient nonlocal means for denoising of textural patterns[J]. IEEE Transactions on Image Processing,2008,17(7)：1083-1092

[20] Coupé P,Yger P,Prima S,et al. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images[J]. IEEE Transactions on Medical Imaging,2008,27(4):425-441

[21] Deledalle C A,Denis L,Tupin F. NL-InSAR:nonlocal interferogram estimation[J]. IEEE Transactions on Geoscience and Remote Sensing,2011,49(4):1441-1452

[22] Zoican S. Speech de-noising system with nonlocal means algorithm[J]. 9thInternational Symposium on Electronics and Telecommunications(ISETC),2010,315-318

[23] Wei D Y,Yin C C. An optimized locally adaptive non-local means denoising filter for cryo-electron microscopy data[J]. Journal of Structural Biology,2010,172(1):211-218

[24] Bonar D,Sacchi M. Denoising seismic data using the nonlocal means algorithm[J]. Geophysics,2012,77(1):A5-A8

(编辑：朱文杰)

Non-local means filtering denoising approach and its application in VSP reverse time migration seismic data

Wang Weihong,Guo Xuebao,Shi Ying

(CollegeofEarthSciences,NortheastPetroleumUniversity,Daqing163318,China)

Low-frequency noise is the inherent property of reverse-time migration (RTM) based on two-way wave equation.Filtering after imaging is widely used to suppress this kind of noise,especially Laplacian filtering method.But the result of Laplacian method depends on angle parameters,the case of rough events and residual noises always exist.In order to improve signal to noise ratio of imaging data of reverse-time migration,Non-local Means (NLM) filtering approach is introduced in this paper,which is used to suppress noise based on the characteristics of event structure of post-stack seismic data,and is applied to the seismic data after Laplacian filtering.By using NLM method,the input seismic data can be divided into noise and data,and the similarity coefficient of different imaging points is applied to realize filtering.For 2D complicated theoretical model,we carried out forward modeling and RTM on VSP data.The results demonstrate that the combination of Laplacian and NLM filtering is better than the result of Laplacian filtering.Moreover,the application of actual VSP seismic data also suggests NLM filtering has advantages in computational accuracy,stability and practicability.

non-local means,noise suppression,reverse time migration,vertical seismic profiling (VSP),Laplacian filtering

2014-09-25;改回日期：2014-12-08。

王维红(1975—)，男，博士，副教授，现主要从事地震资料数字处理方面的研究。

国家自然科学基金项目(41474118)和国家高技术研究发展计划(863)(2012AA061202)资助。

P631

A

1000-1441(2015)02-0165-07

10.3969/j.issn.1000-1441.2015.02.007