基于局部运动学属性参数的窄方位角三维多域插值算法研究与应用

刘春成,杨 锴,杨小椿,薛 冬

(1.中海油研究总院,北京100027;2.同济大学海洋地质国家重点实验室,上海200092)

基于局部运动学属性参数的窄方位角三维多域插值算法研究与应用

刘春成1,杨 锴2,杨小椿1,薛 冬1

(1.中海油研究总院,北京100027;2.同济大学海洋地质国家重点实验室,上海200092)

基于局部运动学属性参数的三维多域插值算法在实际地震数据处理中具有广阔的应用前景。但这种算法通常仅适用于宽方位角三维地震数据,而海洋三维地震数据往往是窄方位角的,这就给传统算法的实现带来了一定的难度。为此,提出了一种适应于窄方位角三维地震数据的三维多域插值与规则化新算法,并设计了相应的实现流程。其策略是通过零偏移距三维频率-波数(F-K)域时间偏移与反偏移,结合零偏移距三维输出道成像方式的共反射面元成像算法(CRS-OIS),获得高信噪比的叠后模型道数据;再通过反叠加生成三维叠前CMP模型道道集,提取其运动学属性参数,基于这些运动学属性参数拟合原始三维叠前数据,从而获得信噪比向模型道逼近的优化后叠前数据体。南海深水区某三维窄方位角地震数据的试应用结果表明,新的算法完全适应窄方位角三维地震数据的特点,有效提高了数据的信噪比和规则化程度,证明了新算法的稳定性和可靠性。

三维多域插值;局部运动学属性参数;窄方位角;共反射面元;多次聚焦

无论在陆地还是海洋三维地震数据处理中,插值与规则化都是一个非常重要的处理环节。陆地资料处理中会有不规则炮检点分布的问题,海洋资料处理中会有方位角校正或者面元均一化的问题。二者都会遭遇目标反射层信噪比太低,需要提高目的层信噪比、改善其资料品质的共同问题。无论实现何种目标,基于三维数据的多域插值都是一个很好的选择方案。在三维多域插值与数据规则化方面,国内外学者根据不同的数学变换算法得到了大量研究成果[1-6]。比较看来,基于局部运动学属性参数的时空域多域插值仍是最为简洁的三维插值与规则化算法。因为该算法直接在时空域内实施,无需在不同数据域之间进行变换,因此易于实现。这方面的典型代表就是基于局部运动学属性参数的多次聚焦多域插值算法[7]与共反射面元多域插值算法[8]。

在三维处理方面,多次聚焦成像算法会遭遇理论上的困难,但是共反射面元成像算法则没有这方面的困难。无论是文献[9]提出的输出道成像方式的共反射面元成像算法(CRS-OIS),还是文献[10]提出的部分CRS叠加算法,都可以顺畅地推广到三维情况。由于CRS-OIS算法将CRS叠加解释为一个大面元偏移到零偏移距(MZO)操作,不再纠结于局部运动学属性参数的物理意义,使得局部运动学属性提取过程得到大幅度简化。二维CRS-OIS算法仅需要2个参数[11],三维CRS-OIS算法仅需要3个参数[12]。当仅实施CRS-OIS算法的第一步,即“沿着共偏移距数据内的局部同相轴进行弥散”时,事实上就已经完成了基于CRS-OIS的数据插值或规则化[13-14]。如果数据本身是比较规则的话,那么第一步弥散后,叠前数据的信噪比将大幅度提高。文献[15]和文献[16]展示了上述思路在中国西部陆上二维、三维地震数据上的应用实例。与传统的三维部分CRS叠加算法需要8个参数相比,三维CRS-OIS算法是一个更为经济的选择。

需要注意的是,无论三维CRS-OIS或三维部分CRS叠加算法都要求输入数据为宽方位数据。因为一旦缺乏足够的方位角信息,三维局部同相波包(3D local coherent wave-packet)的运动学特征就无从把握,这个判断适用于时空域或是任一种数据变换域。这就使得基于运动学属性参数(实际上就是局部同相性)的共反射面元算法或者多次聚焦算法在应对三维窄方位角地震数据时遭遇很大困难。

由于海上地震观测方式的特殊性,到目前为止大多数海洋三维地震数据都是窄方位角的。早期采集的陆地三维数据也是如此,其实陆地宽线地震数据就可以认为是窄方位角三维观测的极端情况。针对这种窄方位角三维数据的插值与规则化究竟如何进行,也是工业界长期以来关注的问题。

我们认为,对于窄方位角三维地震数据,有必要着眼于叠后数据与叠前数据之间的映射关系,引入高精度的数据映射算法来实施其插值、规则化或提高信噪比处理。也就是说,对于局部同相性的追踪必须从叠前回到叠后来进行,在叠后有效提高信噪比之后,再通过高精度数据映射算法获得高品质的叠前数据体。文献[6]首先提出了基于共偏移距相移法偏移-反偏移与CRS-OIS相结合获得高品质叠前道集的思路,并在西部山地低信噪比数据上获得了不错的应用效果;文献[17]则利用信号重构实现信噪比的提高,也是一种很好的思路。

本文将文献[6]的数据映射算法从二维拓展到三维,并结合在三维叠后成像数据体内提取局部波场属性参数,得到了一种适合于三维窄方位角数据的、基于局部运动学属性参数的多域插值与规则化新算法,并设计了相应的实现流程。将该实现流程应用于南海深水某三维窄方位角地震数据的试处理,结果表明该算法完全适应窄方位角三维地震数据的特点,有效提高了数据的信噪比和规则化程度,在实际应用中非常稳定和可靠。

1 三维共偏移距波动方程时间偏移/反偏移算法

波动方程频率-波数域共偏移距时间偏移方法最早由Dubrulle[18]提出,它实质上是一种平面波偏移方法。三维情况下,当偏移距不为零时,记录到的单点绕射旅行时为:

(1)

式中：(xm,z)表示地下一个绕射点的横向和纵向坐标;hx,hy表示x方向和y方向的半偏移距;v表示介质速度;tm表示偏移后的时间。

(1)式描述了地下一个绕射点被等偏移距炮-检观测所照明及接收的时距关系。物理上讲,其时距曲面上某一点斜率可代表某一角度的平面波。Dubrulle[18]认为将这些平面波相移到时间轴的起点,应用成像条件,即可得到某一个平面波的叠前时间偏移结果;将所有平面波偏移结果累加在一起,即可得到最终叠前时间偏移的结果。考虑到三维非零偏移距的波动方程偏移/反偏移对计算成本有相当的要求,本文仅讨论零偏移距情形,因此(1)式变为:

T(tm,xm,ym,hx=0,hy=0)

(2)

(2)式对x,y求偏导数,可以得到梯度向量:

(3)

与二维情况类似,只要将三维空间中不同斜率的平面波分别进行相移处理,再对所有频率的平面波求和,即可得到(xm,ym,tm)处的三维时间域成像结果。如果在(xm,ym)处向上引一条垂线作为新的t轴,那么相移量τ即为切平面在时间t轴上的截距,由公式τ=Td-kx(x-xm)-ky(y-ym)定义。因此,零偏移距三维频率-波数域相移偏移可以通过如下3步实现:

1) 将输入的原始零偏移距道集波场记为：

(4)

式中:x,t,h分别代表空间、时间和半偏移距坐标;tm代表时间偏移中所用到的“时间深度”,tm=0意味着是在地表记录到的波场。由于h=0,故后面的波场符号中将h=0的部分省略,对其进行三维Fourier变换,得到:

ei(ω t-kxx-kyy)dtdxdy

(5)

2) 按照(3)式对输入波场进行相移处理,即对时间深度方向上进行延拓:

(6)

3) 应用成像条件t=0,再将所有频率进行求和,然后进行三维Fourier反变换,得到偏移后的结果:

(7)

按照完全类似的过程,可以推导出相应的三维零偏移距时间相移反偏移公式。它与刚刚讨论过的叠前时间相移偏移具有类似的形式,区别仅在于相移因子的符号与偏移时相反。它需要将上行波方程正向外推到地表,然后提取地表处的波场值,从而得到地震记录。因此,反偏移的处理流程同样可以归纳为3步:

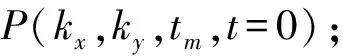
Yang等[19]的测试表明,只要使用同样的速度对共偏移距数据体实施偏移/反偏移,反偏移后所得数据的运动学和动力学特征与原始数据相比几乎没有任何影响。即便在速度不是很精确时,上述性质依然成立。这是一个重要的性质,它保证了频率-波数域时间偏移/反偏移可以作为地震数据映射的一个可靠工具用于随后的处理流程中。

2 三维零偏移距剖面的3D-CRS-OIS局部运动学属性参数搜索

在得到三维零偏移距时间偏移剖面后,为了提高该数据体的信噪比,将该数据体输入到三维CRS-OIS算法。下面对Yang等[12]提出的3D-CRS-OIS三参数属性参数搜索策略作简要回顾。Yang等[9]基于统一成像理论对CRS叠加方法做出了一个重要的改进,认为其本质上就是一个大面元的MZO算法。基于上述认识,Yang等[11-12]提出了输出道观点的二维、三维共反射面元(CRS-OIS)叠加方法。二维情况下,只需2个参数(常规CRS叠加需要3个);三维情况下,只需3个参数(常规CRS叠加需要8个)。相比常规CRS叠加算法,新的CRS-OIS叠加算法在计算成本方面有相当的优势。这里简要回顾一下其局部运动学属性参数的搜索过程。

首先,对传统的CRS旅行时曲线作零偏近似,得:

(8)

式中:m,m0是中点矢量;h是偏移距矢量;α是入射角;λ是方位角;v0是近地表速度;KN是波前曲率。对于(8)式我们可以继续应用局部球面近似，使得KN=1/rn,然后令rn→∞,有:

(9)

首先利用方程(9)进行二维搜索,得到方位角λ和入射角α;然后将λ,α代入方程(8),进行一维搜索得到KN。这样,在得到这三种局部波场属性参数之后,基于三维局部相干同相面构造3D-CRS-OIS算子,即可完成三维CRS-OIS叠加。

3 基于局部运动学属性参数的窄方位角三维多域插值算法实现流程

当通过三维F-K域时间偏移、三维零偏移距CRS-OIS、三维F-K域时间反偏移这样连续三步的处理获得了信噪比大幅提高的三维零偏移距数据后,接下来将通过反叠加获得高信噪比的三维模型道集。所谓反叠加指的是使用和初始叠加时完全相同的叠加速度实施反投影处理,从一个叠加剖面内的一个叠加道出发,获得一个叠前CMP道集。这是一个叠加的逆过程,按照双曲线轨迹实施反投影可以获得高信噪比的叠前CMP道集。由于反叠加依然是基于初始叠加的叠加速度实施的,这样可以保证模型道集与原始数据有最大的运动学意义上的相似性。

获得三维模型道集之后,我们认为其运动学特征可以代表原始数据,因此通过类似于常规CRS叠加获得属性搜索的过程获得模型道集的运动学特征(斜率信息与曲率信息)。这时,就可以将原始叠前数据按照模型道集的运动学特征进行合理的加强,可以自然获得合理的插值、规则化或者噪声压制的效果。上述思路可以总结为如图1所示的实现流程。

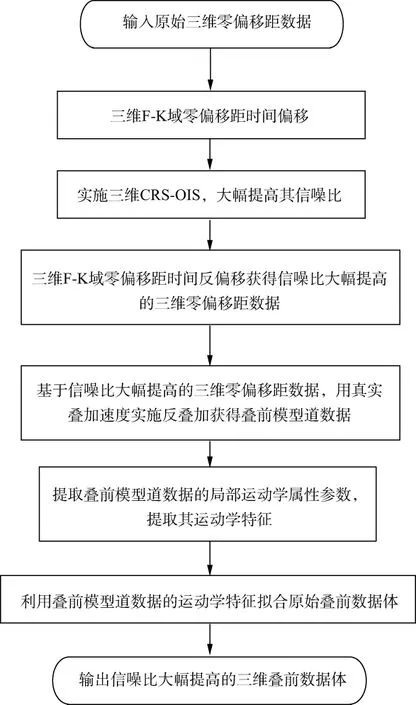
图1 基于局部运动学属性参数的窄方位角三维多域插值算法实现流程

4 南海深水LH工区三维地震数据试应用算例

试应用三维实际地震数据来自南海深水LH工区,采集于2011年,采用双源6缆的采集方式,炮距25.0m,道距12.5m。图2a显示了LH三维的CDP覆盖次数,共13000炮。由于每炮只有6缆接收(如图2b所示),属于典型的窄方位角三维数据。LH三维单次覆盖面积约90km2,最高覆盖次数156次。

4.1 针对窄方位角地震数据的处理步骤

如前所述,三维输出道方式的CRS叠加(3D-CRS-OIS)要获得成功应用的前提是要得到品质较好的单次共方位角共偏移距(CACOG)剖面,所谓品质较好是指目标反射层在单次CACOG剖面内无论是纵测线还是横测线方向都要有一定的信噪比和同相性(哪怕是很弱的)。如果目标反射层在单次CACOG剖面上无法辨认,那么3D-CRS-OIS算法在该数据空间内的搜索将无法得到反射信息的同相性,信噪比的提高也就失去了前提。而LH三维由于仅有6缆接收,恰恰属于窄方位角数据,很难抽出满意的CACOG剖面供3D-CRS-OIS算法使用。

图2 LH三维CDP覆盖次数(a)及原始单炮记录(b)

现在的问题是,如果一定要对目的层信息进行有效增强,就必须尽一切可能在其它道集内捕捉该反射层的同相性。那么对于窄方位角三维数据而言我们只有一个选择,即在CMP道集内甚至是叠加剖面上才能扑捉到最连续的反射信息。明确了窄方位角地震数据的特点之后,我们便可制定出具有针对性的处理步骤:

1) 对三维初始叠加剖面实施叠后相移时间偏移,使用初始叠加速度场即可;

2) 在叠后相移时间偏移后的剖面上实施三维CRS-OIS处理,即将该剖面视为一个CACOG剖面来处理,这个计算成本是非常小的;

3) 对三维CRS-OIS处理后的剖面实施叠后相移时间反偏移,注意一定要采用与第1步中相同的初始叠加速度场;

4) 基于第3步得到的剖面实施反叠加,得到高信噪比的三维叠前道集作为模型道;

5) 基于第4步得到的三维叠前道集,实施局部运动学属性参数搜索;

6) 将第5步得到的属性参数用于拟合原始叠前数据的运动学特征,使得原始叠前数据的信噪比向模型道逼近;

7) 输出优化逼近后的叠前数据体,作为提高信噪比与规则化流程处理后的结果供后续的成像等处理模块使用。

4.2 LH海洋三维地震数据试处理结果

由于篇幅所限,这里仅给出LH三维零偏移距数据体中的部分纵测线剖面的处理结果。图3a显示了4条纵测线的初始叠加剖面;图3b是这4条纵测线的三维零偏移距FK域叠后时间偏移剖面;图3c给出了基于图3b实施三维CRS-OIS处理后的剖面,可以看到信噪比有明显提高;图3d为基于图3c实施三维零偏移距F-K域时间反偏移之后的剖面。由图3d可以看到,在剖面信噪比和有效波连续性得到明显提高的同时,绕射波也得到了很好的保护。这种保护对后续的反叠加处理是非常有利的。

在得到图3d所示反偏移处理后的高质量的叠加剖面后,对该剖面实施“反叠加”处理,得到图4所示的高信噪比叠前CMP道集,作为模型道供后续处理使用。所谓“反叠加”指的是使用与叠加时完全相同的叠加速度实施反投影处理,从一个叠加剖面内的一个叠加道出发,获得一个叠前CMP道集。由于在叠加处理时是完全按照双曲线规律去叠加的,所以这里的反叠加也直接按照双曲线轨迹实施反投影,即可获得高信噪比的叠前CMP道集。

基于图4所示的三维模型道CMP道集进行局部运动学属性参数搜索,图5a和图5b是得到的斜率剖面和曲率剖面。显然,这些运动学属性参数剖面完全体现了三维叠前CMP数据的运动学特征。

将图5所示的运动学属性参数剖面用于拟合原始叠前数据的运动学特征,即对原始叠前数据实施运动学意义上的相干加强处理。拟合时的算子孔径是一个关键的参数,算子孔径越大,原始数据将被拟合得越接近模型道集,反之则更为接近原始数据。通过反复测试,我们选择了20道作为算子的横向孔径。图6给出了处理前的CMP道集(图6a)和算子孔径为20道时的拟合结果(图6b),对比可见在信噪比得到大幅提高的同时,原始道集本身的特点依然得到保留,这种优化逼近后的数据用于后续的偏移速度分析和构造成像处理无疑是非常有利的。

图3 LH三维4条纵测线的初始叠加(a)、叠后时间偏移(b)、三维CRS-OIS(c)及反偏移(d)处理剖面

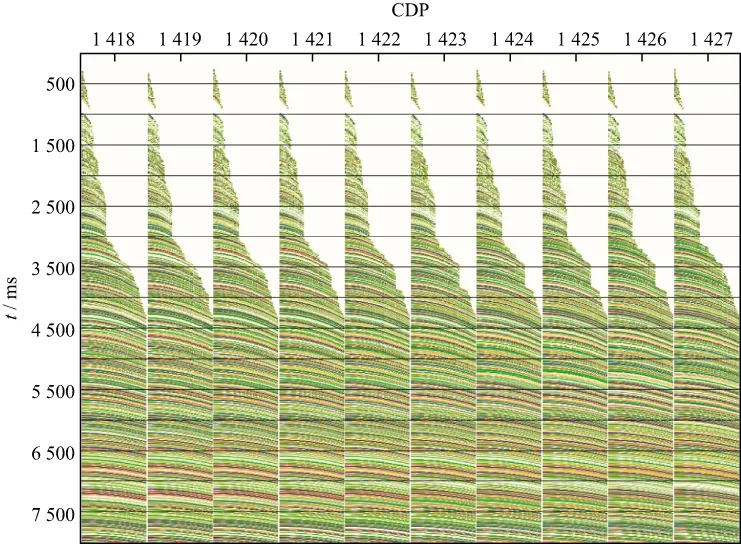
图4 基于反偏移处理后剖面(图3d)实施反叠加重建得到的若干高信噪比叠前CMP道集

由于海洋地震数据一般没有缺失道的问题,所以这里的插值效果无法展示。注意基于模型道提取的运动学特征在空间上是连续、无间断的,因此可以预见如果有缺道出现,在拟合过程中将自然的将其插值出来,其效果将类似于文献[13]和文献[15]的插值结果。

图7a和图7b以及图8a和图8b分别展示了纵测线4722和纵测线4762处理前的原始CMP道集与优化逼近后的CMP道集对比;图9a和图9b 以及图10a和图10b分别展示了两处(纵测线4622-横测线2000及纵测线4762-横测线2000)处理前、后的速度分析效果对比;图11a和图11b以及图12a和图12b则分别展示了纵测线4720和纵测线4758处理前的原始CMP叠加剖面与优化逼近后的CMP叠加剖面对比。由LH三维零偏移距数据体中部分纵测线剖面的这些处理结果可以明显看出,本文提出的基于局部运动学属性参数的多域插值与规则化算法适用于三维窄方位角数据,最终的优化逼近处理结果得到了数据规则、信噪比大幅度提高的叠前数据道集和叠后剖面。

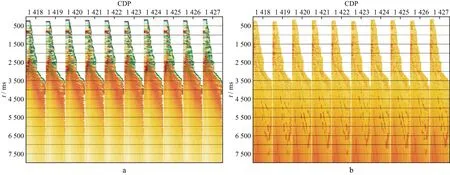
图5 基于图4搜索得到的运动学属性参数剖面

图6 处理前的CMP道集(a)和算子孔径为20道时的运动学特征拟合结果(b)对比

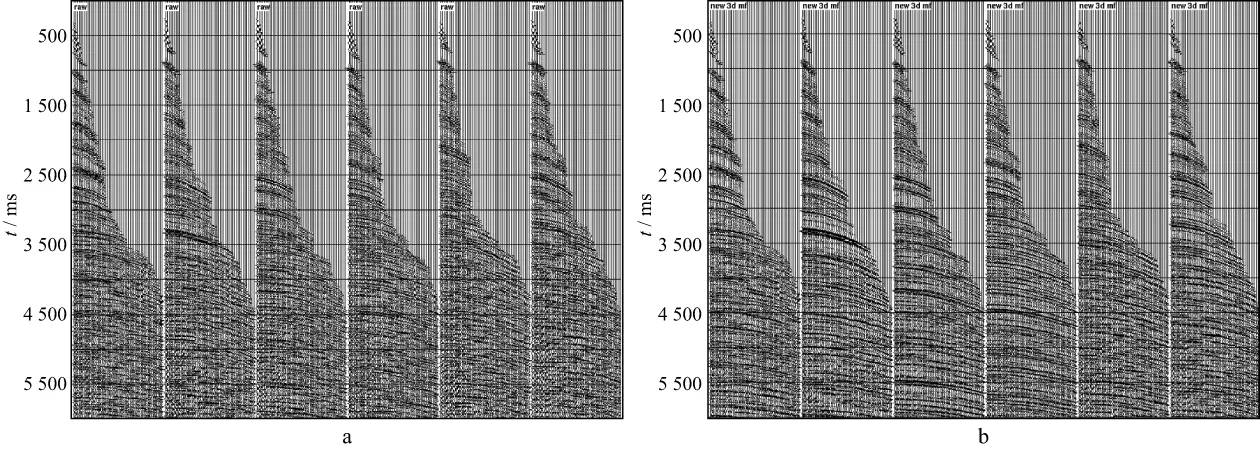
图7 纵测线4722处理前(a)、后(b)CMP道集对比

图8 纵测线4762处理前(a)、后(b)CMP道集对比

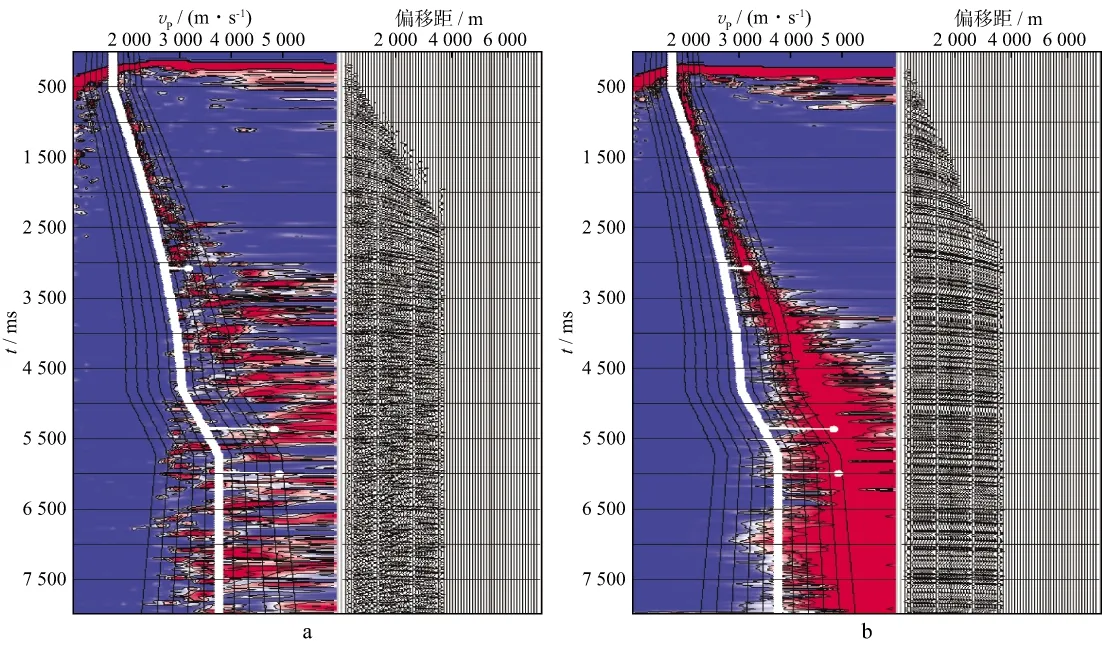
图9 处理前(a)、后(b)速度分析效果对比(纵测线4622-横测线2000处)

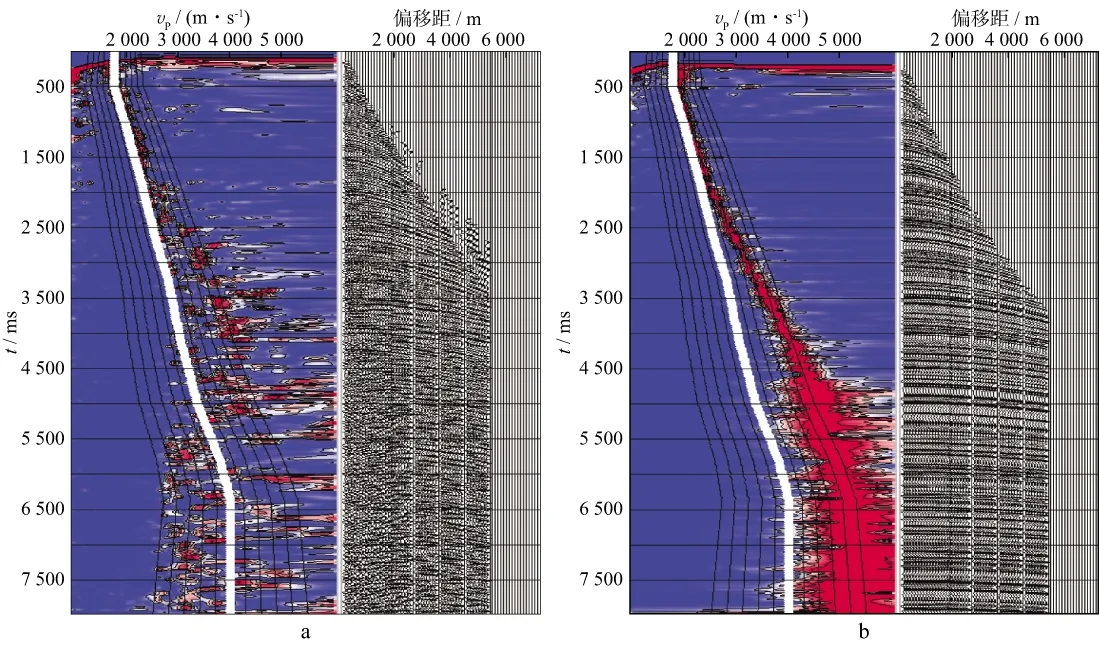
图10 处理前(a)、后(b)速度分析效果对比(纵测线4722-横测线2000处)

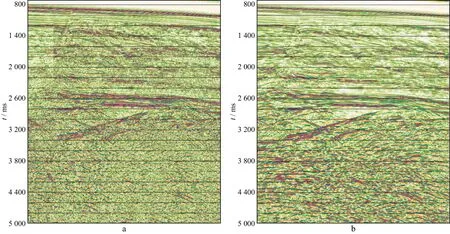
图11 纵测线4720处理前(a)、后(b)的叠加剖面

图12 纵测线4758处理前(a)、后(b)的叠加剖面

5 结论与认识

由于海洋地震采集方式的特殊性,海洋三维地震数据采集得到的数据目前还是以窄方位角为主,这就给基于局部运动学属性参数的三维插值与规则化算法的实现带来了一定的难度,因为这种算法通常仅适用于宽方位角三维数据。为此,本文提出了一种基于局部运动学属性参数的窄方位角三维多域插值新算法。首先实施三维相移法叠后时间偏移,获得初始叠后时间偏移剖面;对叠后时间偏移剖面实施三维CRS-OIS,加强该剖面的信噪比;再对其进行三维相移法叠后时间反偏移,获得高品质的三维叠加剖面;对所获高品质叠后数据实施反叠加,回到叠前生成模型道道集,仔细评估模型道集的可信度,重复上述过程;在获得可信的模型道剖面的基础上,提取其运动学属性参数;基于这些运动学属性参数优化拟合原始三维叠前数据的运动学特征。显然,最终的优化拟合结果能够得到一个数据规则、信噪比大幅提高的叠前数据体,基于该三维叠前数据体实施后续处理将有效提高成像结果的可解释性。对南海深水LH工区窄方位角三维地震数据试应用的处理结果表明,上述新算法完全适应窄方位角三维地震数据的特点,有效提高了数据的信噪比和规则化程度,且在实际应用中非常稳定和可靠。

值得指出的是,在上述算法实现流程中,所有的速度信息都使用了原始的叠加速度信息,因此上述处理将不会对原始三维叠前数据的运动学特征有任何改造。由于海洋地震数据不存在缺失道现象,因此本文的试应用结果仅显示出了信噪比大幅提高的处理效果,而无法展示新算法的插值效果,有待下一步在应用于陆地三维地震数据的处理实例中展示其噪声压制和数据插值的双重效果。该新算法及其实现流程同样适用于陆地窄方位角三维地震数据与宽线地震数据。

[1] Xu S,Zhang Y,Lambaré G.Antileakage Fourier transform for seismic data regularization in higher dimensions[J].Geophysics,2010,75(6):WB113-WB120

[2] Naghizadeh M,Sacchi M.Multidimensional de-aliased Cadzow reconstruction of seismic records[J].Geophysics,2013,78(1):A1-A5

[3] Wang X,Wang H Z,Zhou D H,et al.Minimizing ellipsoidal norm seismic data interpolation with radon spectrum constraints[J].Expanded Abstracts of 73rdEAGE Annual Conference,2011,A046

[4] 辛可锋,王华忠,王成礼,等.叠前地震数据的规则化[J].石油地球物理勘探,2002,37(4):311-317 Xin K F,Wang H Z,Wang C L,et al.Regularization of pre-stack seismic data[J].Oil Geophysical Prospecting,2002,37(4):311-317

[5] 刘玉金,李振春.局部平面波模型约束下的迭代加权最小二乘反演三维地震数据规则化[J].石油地球物理勘探,2012,47(3):418-424 Liu Y J,Li Z C.Three dimensional data regularization by iteratively re-weighted least squares inversion based on the local plane wave model[J].Oil Geophysical Prospecting,2012,47(3):418-424

[6] 杨锴,王毓玮,王华忠,等.基于偏移/反偏移的地震数据映射方法[J].石油地球物理勘探,2008,43(1):16-22 Yang K,Wang Y W,Wang H Z,et al.Seismic data mapping based on migration/inverse-migration[J].Oil Geophysical Prospecting,2008,43(1):16-22

[7] Buzlukov V,Landa E.Imaging improvement by prestack signal enhancement[J].Geophysical Prospecting,2013,61(6):1150-1158

[8] Hoecht G,Ricarte P,Bergler S,et al.Operator-oriented CRS interpolation[J].Geophysical Prospecting,2009,57(6):957-981

[9] Yang K,Wang H Z,Ma Z T.An output imaging scheme of the common reflection surface stack[J].Journal of Seismic Exploration,2005,14(1):131-154

[10] Baykulov M,Gajewski D.Prestack seismic data enhancement with partial common-reflection- surface (CRS) stack[J].Geophysics,2009,74(3):V49-V58

[11] Yang K,Wang H Z,Dong L G,et al.An output imaging scheme of the common reflection surface stack:applications to real data[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006,2529-2533

[12] Yang K,Jiang X G.Application of an output imaging scheme of 3D common reflection surface stack (3D CRS-OIS) to 3D real data acquired in Chinese mountainous area[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010,3614-3618

[13] Ni Y,Yang K,Wang Y X.Noise suppression and data interpolation with 3D CRS-OIS[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012,2529-2533

[14] 杨锴,倪瑶.基于稳相原理与克希霍夫统一成像理论对射线束类成像方法的一种新观点:以CRS叠加为例[C]∥CPS-SEG北京2014国际地球物理会议摘要.北京：石油出版社,2014:490-493 Yang K,Ni Y.A new insight of beam-ray imaging method based on the stationary-phase principle and unified Kirchhoff imaging theory:for example of CRS stack[C]∥CPS-SEG Beijing 2014 International Geophysical Conference.Beijing:Petroleum Press,2014:490-493

[15] 童思友,杨锴,孔剑冰,等.利用CRS-OIS实现噪声压制与数据插值[J].同济大学学报(自然科学版).2010,38(5):753-757 Tong S Y,Yang,K,Kong J B,et al.Noise suppression and data interpolation by using CRS-OIS[J].Journal of Tongji University(Natural Science),2010,38(5):753-757

[16] 倪瑶,杨锴.基于GPU计算平台实现三维输出道方式的共反射面元(3D-CRS-OIS)叠加[J].石油地球物理勘探,2013,48(1):57-65 Ni Y,Yang,K.3D common reflection surface stack algorithm based GPU with the output imaging scheme(3D-CRS-OIS)[J].Oil Geophysical Prospecting,2013,48(1):57-65

[17] 刘春成,刘畅,王大利,基于重构信号模型的去噪技术[J].铀矿地质,2011,27(3):173-179 Liu C C,Liu C,Wang D L.A new technology for noise removal in the model-based signal reconstruction[J].Uranium Geology,2011,27(3):173-179

[18] Dubrulle A.Numerical methods for the migration of constant-offset sections in homogeneous and horizontally layered media[J].Geophysics,1983,48(9):1195-1203

[19] Yang K,Chen B S,Wang X J,et al,Handling conflicting dip problem in CRS stack via combination of CRS-OIS and migration/demigration[J].Geophysical Prospecting,2012,60(2):255-269

(编辑：朱文杰)

A multi-domain interpolation algorithm for 3D narrow-azimuth seismic data based on the local kinematic attributes and its application

Liu Chuncheng1,Yang Kai2,Yang Xiaochun1,Xue Dong1

(1.CNOOCResearchCenter,Beijing100027,China; 2.StateKeyLaboratoryofMarineGeology,TongjiUniversity,Shanghai200092,China)

The local kinematic attributes based multi-domain interpolation algorithm has huge potential in real applications.However,such kind of algorithm is always not applicable for 3D narrow-azimuth seismic data.In this paper,a novel multi-domain interpolation algorithm for 3D narrow-azimuth seismic data based on the local kinematic attributes is developed.The basic idea of this algorithm is to combine the zero-offset 3D frequency-wavenumber domain time migration/de-migration method and the zero-offset 3D-CRS-OIS method to achieve high signal-noise-ratio zero-offset post-stack model trace data.Then,a 3D model CMP gather can be generated with a smearing style de-stacking operator.The local kinematic attributes of 3D model CMP gathers will be extracted to guide for the optimization of the raw 3D CMP gathers.Thus a practical workflow is designed and applied to deep-water 3D seismic data acquired in the South China Sea.The application result demonstrated the robustness and high efficiency of the proposed workflow and algorithm.

3D multi-domain interpolation,local kinematic attributes,narrow azimuth,common reflection surface,muliti-focusing

2014-01-05;改回日期：2014-07-20。

刘春成(1962—)，男，教授级高级工程师，研究方向为地震资料解释、处理与储层预测。

杨锴(1972—)，男，博士，教授，研究方向为地震波的反演、成像及储层随机建模。

国家科技重大专项项目(2011ZX05025-001-03)、国家自然科学基金项目(41274117)和海洋地质国家重点实验室自主课题(MG20130304)共同资助。

P631

A

1000-1441(2015)03-0282-10

10.3969/j.issn.1000-1441.2015.03.006