孔缝腔体内传输线负载上最大感应电流的研究

顾长青 王 斌 李 茁 牛臻弋 曹丽霞 林志斌

孔缝腔体内传输线负载上最大感应电流的研究

顾长青 王 斌 李 茁 牛臻弋 曹丽霞 林志斌

（南京航空航天大学电子信息工程学院，江苏南京210016）

应用多端口网络理论，把孔缝屏蔽腔和腔内传输线一起等效成多天线系统，基于天线的互易定理，提出了快速预测孔缝屏蔽腔内多导体传输线负载上的最大感应电流的方法.由于避免了孔缝屏蔽腔内传输线负载上感应电流的直接全波分析，计算效率显著提高.文中计算了矩形屏蔽机箱上开孔尺寸与形状、机箱大小、传输线在机箱内位置等参数改变下屏蔽机箱内传输线负载上的最大感应电流响应.与直接全波仿真结果比较，验证了方法的有效性.

孔缝屏蔽腔；传输线；互易定理；最大感应电流

引 言

在复杂的空间电磁环境中，作为传输信号的载体——传输线（如线缆、线束、印制微带线等）极容易受到外来电磁波的耦合作用，它是外来电磁波传导进入设备或系统内部的重要通道之一.为了保证设备或系统安全可靠地工作，研究场线耦合的电磁效应是有非常重要的意义.

除了电磁场数值方法［1－2］，常常采用传输线BLT（Baum－Liu－Tesche）方程分析置在自由空间的传输线的直接电磁效应问题［3－4］，而置在孔缝屏蔽腔（如电子设备机箱、飞机舱室等）内传输线的间接电磁效应问题，则多采用基于电磁拓扑（Electromagnetic Topology，EMT）理论的技术进行分析［5］.该方法是在“近似良好屏蔽”的条件下，首先用场求解器计算忽略传输线存在时传输线所在位置的场分布.然后提取传输线附近的场分布作为场－线耦合模型中孤立传输线的激励，进而建立BLT方程来分析沿传输线传播的导行场.和电磁场数值方法相比，具有计算速度快的优势，但缺点是计算精度较差.

为了避免设备或系统欠电磁兼容性设计，近年来，人们非常关注场线最大耦合的预测和分析研究.2011年Lagos等人提出了一种BLT方程结合优化算法的混合计算方法［6－7］，在频率和印制微带线端接负载一定时，计算任意极化电磁波全空间照射下微带线负载上的最大感应电流.由于每一入射方向、极化的电磁波和每次改变传输线的负载都要进行重新计算，即使每次计算用时非常少，但是总时间仍是很大的.为了缓解大计算量的问题，2013年Vanhee等人提出了一种基于天线互易定理的全波快速分析方法［8］，计算在外来平面波激励下置于接地平面上方的多导体传输线端接负载上的最大感应电流.该分析方法分为两步实现：在第一步中，将多导体传输线系统看成是多天线系统，用最少次数的全波仿真对其远场辐射特性进行完整地表述；在第二步中，该远场信息用来有效评估任意极化和入射方向的电磁波在传输线端接负载上的感应电流.这样通过负载上的感应电流大小排序求出其最大值.目前仿真预测孔缝屏蔽腔内传输线的最坏间接电磁效应未见有报道.

文章将孔缝屏蔽腔和腔内传输线一起等效成多天线系统，使用文献［8］提出的基于天线互易定理的全波快速分析方法，应用于孔缝屏蔽腔内多导体传输线负载上最大感应电流的快速预测，计算了矩形屏蔽机箱上开孔尺寸与形状、机箱大小、传输线在机箱内位置等参数改变情况下屏蔽机箱内传输线负载上的最大感应电流响应.

1 方法原理

不失一般性，图1给出了多导体传输线置在孔缝屏蔽腔内的结构示意图.基于多端口网络理论［9］，多导体传输线和孔缝屏蔽腔一起等效成多天线系统的多端口网络，传输线的每一负载端接处等效为一天线的激励端口，这样所有负载和激励源可以统一地看作是与多天线系统连接的另一多端口网络.

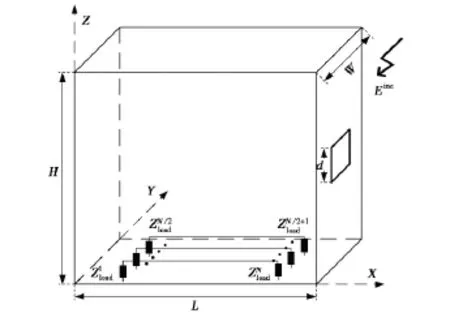
图1 孔缝屏蔽腔内多导体传输线的结构示意图

在图1中，已假设多天线系统的天线数目为N根据文献［8］提出的基于互易定理的全波快速预测方法，求解给定频率条件下不同极化、不同入射方向外来电磁波在传输线负载上的最大感应电流响应可以分为下列步骤.

1）第i天线工作在发射模式（端口上加馈源），其它天线端口开路时，使用全波方法（例如矩量法）计算辐射电场Eff，iopen（θ，φ）以及其余第j（j≠i｜j＝1，2，…，N）天线端口上的电压Vjt，open（下标t表示天线工作在发射模式）.

2）根据公式

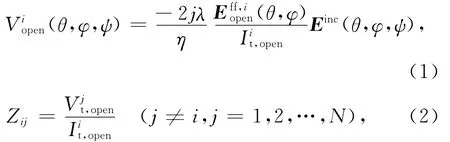
分别计算第i天线工作在接收模式时全空间不同极化外来电磁波在馈电端口感应的开路电压Viopen（θ，φ，ψ）以及第i天线与第j（i，j＝1，2，…，N）天线之间的端口互阻抗Zij，Zij与天线工作模式无关.式中，Einc（θ，φ，ψ）为外来平面电磁波的电场矢量，Iit，open为第i馈电端口上加激励时其端口上的电流，λ为工作波长，η为自由空间的特性阻抗，（θ，φ）为球坐标系中方向角，ψ为极化角.

3）对步骤1）和步骤2）进行i从1至N的循环运算，得到N天线系统的激励电压矩阵Vopen（θ，φ，ψ）和端口的阻抗矩阵Zant.Vopen向量和Zant矩阵的形式为：

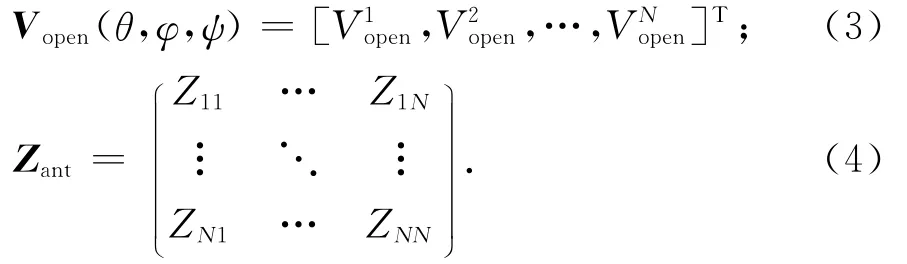
由互易定理知，Zant与天线工作模式无关，不论工作在接收模式还是工作在发射模式，其阻抗元素是一样的，另外Zij＝Zji.

4）计算外来电磁波经孔缝屏蔽腔耦合后在传输线负载上的感应电流响应天线端口上的电流向量Ir和电压向量Vr通过下列式子计算得到（下标r表示天线工作在接收模式）

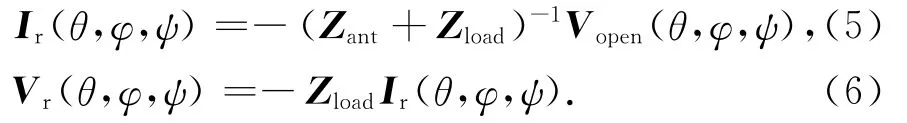
式中：

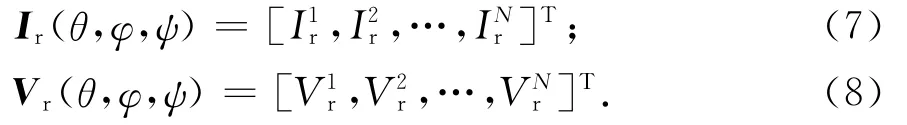
Zload＝diag（Z1load，Z2load，…，ZNload）是由传输线负载阻抗构成的对角矩阵.

5）在求出所有极化和方向的Ir（θ，φ，ψ）以后，通过排序的方法找出传输线各负载上最大电流，即

max｛｜Iir（θ，φ，ψ）｜｝（i＝1，2，…，N）.（9）

对于给定的一组负载，如果仅仅要求预测某一个负载上的最大感应电流时，只需要一次全波仿真即可完成.

2 数值算例

为了简单起见，文中所用算例中多导体传输线负载均取为50Ω，传输线近似为未被包裹的细裸导线.

2.1孔缝屏蔽机箱内的单导体传输线

选用图1给出的理想导体孔缝机箱模型，尺寸为473mm×185mm×475mm，正方形小孔开在机箱正面的正中央，边长为3cm.机箱内单根传输线置在机箱底面的正中央，线长30cm，离机箱底面5 cm，直径0.5mm.

图2是单根传输线负载Z1load上的最大感应电流响应，和FEKO软件直接计算的结果比较可以看出，基于互易定理的全波快速方法预测外来平面波激励下置于屏蔽腔内传输线负载上的最大感应电流具有良好的准确性.图3为改变开孔边长大小时负载Z1load上的最大感应电流曲线，从图中可以看出，随着开孔尺寸变大，最大感应电流相应地变大，这是因为随着孔尺寸变大，从机箱上孔进入机箱内的电磁能量也变大，相应地耦合到传输线负载上的最大感应电流因能量增加而变大.图4为开孔面积不变而开孔形状分别为圆形、方形、3cm×3／cm水平矩形和3／cm×3cm竖直矩形负载Zl1oad上的最大感应电流，图中低频段最大感应电流基本相同，而接近1GHz时竖直矩形孔感应电流最大，水平矩形孔感应电流最小，方形孔和圆形孔最大感应电流基本相同.图5是473mm×473mm×475mm大机箱、473mm×185mm×475mm正常机箱和473mm×185mm×185mm小机箱内传输线负载Zl1oad上的最大感应电流，从图中可以看出，由于方孔尺寸相同，小机箱中的电磁能量密度比较大，最大感应电流在仿真频率范围内普遍大于正常机箱情况，而大机箱由于腔内多模式谐振造成在多个频点处过冲的最大感应电流.图6为机箱正面竖直排列三个方孔情况的最大感应电流曲线，中间方孔的尺寸、位置与图2算例中相同，另两个相同尺寸的方孔位置与中间方孔相距10cm.

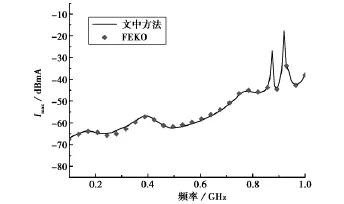
图2 机箱中传输线最大感应电流

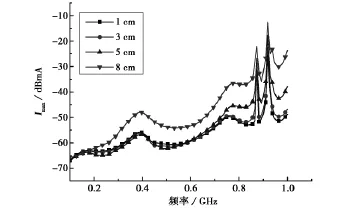
图3 改变开孔边长大小

2.2孔缝屏蔽机箱内的多导体传输线

在图1孔缝屏蔽机箱的多导体传输线模型中，相同传输线的数目取为3.中心传输线依旧放置于底面中央，其余两根传输线放置在离中心线两边各1cm处，机箱、方孔和传输线的参数与图2算例中相同.图7为3根传输线上各端负载上的最大感应电流曲线.

图4 改变开孔形状

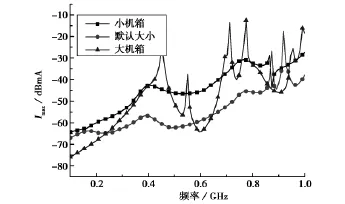
图5 改变机箱大小

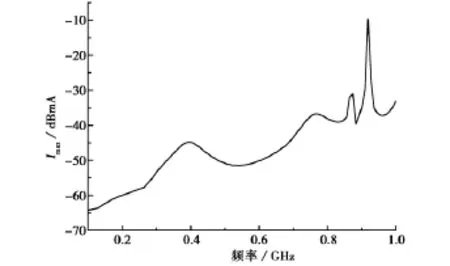
图6 三个方孔情况

在上例基础上，图8给出了孔缝屏蔽机箱中另一组3根相同传输线（如图9所示）上的最大感应电流曲线.其中，第1根传输线置在机箱底面上的正中央位置，第2根传输线置在开孔对面机箱壁上的正中央位置，第3根传输线置在与开孔壁相邻机箱侧壁的正中央位置.从图中可以看出，除了端口5、6之外，其它端口上最大感应电流相差不大.

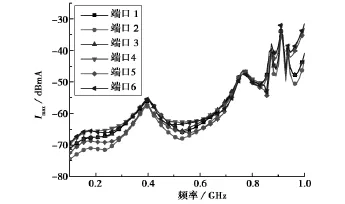
图7 底面三根传输线上最大感应电流

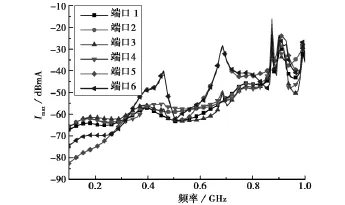
图8 三个面上传输线最大感应电流

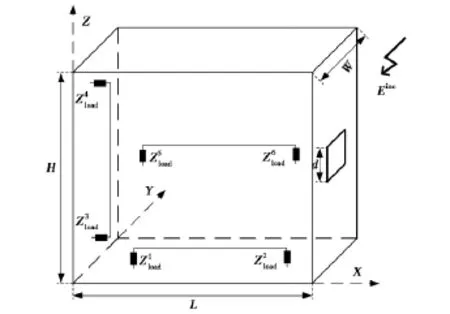
图9 三个面上接传输线示意图

3 结 论

文中方法对于传输线所处的环境不需要进行限定，无论是处在自由空间（可以包含接地线或接地平面）还是处在任意形状的孔缝屏蔽腔内，孔缝屏蔽腔上既可以有单个孔缝又可以是阵列孔缝；传输线既可以是裸线又可以是包裹线或双绞线等.由于只需要N次全波仿真即可得到多导体传输线的所有辐射特性，并且和端接负载的大小、类型、电路拓扑结构无关，相比于直接使用全波仿真方法，文中方法计算时间大大减少；数值算例表明采用基于天线互易定理的全波快速方法预测孔缝屏蔽腔内多导体传输线负载上最大感应电流响应是高效、可行的.

［1］ FELIZIANI M，MARADEI F.Field－to－wire coupling using the finite element－time domain（FE－TD）method［J］.IEEE Transactions on Magnetics，1995，31（3）：1586－1589.

［2］ BERENGER J P.A multiwire formalism for the FDTD method［J］.IEEE Transactions on Electromagnetic Compatibility，2000，42（3）：257－264.

［3］ TESCHE F M.On the analysis of a transmission line with nonlinear terminations using the time－dependent BLT equation［J］.IEEE transactions on Electromagnetic Compatibility，2007，49（2）：427.

［4］ BAUM C E，LIU T K，TESCHE F M.On the analysis of general multiconductor transmission－line networks［J］.Interaction Note，1978，350：467－547

［5］ KIRAWANICH P，TZEREMES G，CHRISTODOULOU C，et al.Electromagnetic wave penetrating through apertures：comparison of electromagnetic topology technique with FDTD method［J］.IEEE Antennas and Wireless Propagation Letters，2005，4：151－154.

［6］ LAGOS J L，FIORI F.Worst－case induced disturbances in digital and analog interchip interconnects by an external electromagnetic plane wave——Part I：modeling and algorithm［J］.IEEE Transactions on E－lectromagnetic Compatibility，2011，53（1）：178－184.

［7］ LAGOS J L，FIORI F.Worst case－induced disturbances in microstrip interchip interconnects by an external electromagnetic plane wave——part II：analysis and validation［J］.IEEE Transactions on Electromagnetic Compatibility，2011，53（2）：491－500.

［8］ VANHEE F，PISSOORT D，CATRYSSE J，et al.Efficient reciprocity－based algorithm to predict worst case induced disturbances on multiconductor transmission lines due to incoming plane waves［J］.IEEE Transactions on Electromagnetic Compatibility，2013，55（1）：208－216.

［9］ HARRINGTON R F，HARRINGTON J L.Field Computation by Moment Methods［M］.Oxford University Press，1996.

［10］ 王利萍，周东方，彭 强，等.基于拓扑网络的屏蔽腔体内置微带线响应分析［J］.电波科学学报，2014，29（1）：321－327.

WANG Liping，ZHOU Dongfang，PENG Qiang，et al.Response analysis of microstrip lines in shielding cavity based on topological network［J］.Chinese Journal of Radio Science，2014，29（1）：321－327.（in Chinese）

［11］ STOLLE R.Electromagnetic coupling of twisted pair cables［J］.IEEE Journal on Selected Areas in Communications，2002，20（5）：883－892.

［12］ 贾 锐，王庆国，程二威，等.混响室“全向辐照”电磁环境场线耦合规律分析［J］.电波科学学报，2014，29（2）：385－390.

JIA Rui，WANG Qingguo，CHENG Erwei，et al.A－nalysis of field－to－wire coupling in full radiation environment in reverberation chamber［J］.Chinese Journal of Radio Science，2014，29（2）：385－390.（in Chinese）

［13］ KILDAL P S.Equivalent circuits of receive antennas in signal processing arrays［J］.Microwave and Optical Technology Letters，1999，21（4）：244－246.

［14］ 刘顺坤，聂 鑫，陈向跃.电磁脉冲对电缆耦合问题的理论研究［J］.电波科学学报，2010，25（2）：348－352.

LIU Shunkun，NIE Xin，CHEN Xiangyue.Numerical study on cable coupling effects excited by electromagnetic pluse［J］.Chinese Journal of Radio Science，2010，25（2）：348－352.（in Chinese）

Analysis of the maximum induced current of transmission line in cavity with apertures

GU Changqing WANG Bin LI Zhuo NIU Zhenyi CAO Lixia LIN Zhibin
（College of Electronic and Information Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing Jiangsu 210016，China）

A novel method using multi－port network theory，and considering the transmission line in cavity with apertures as an multi－antenna system is proposed based on reciprocity theory to fast predict the maximum induced current at the ports of the transmission line in cavity.Since this method does not use the direct full－wave simulation algorithm to calculate the induced current，the calculation efficiency is obviously improved.The maximum induced current of different situation is discussed.The result is compared to the direct full－wave simulation method，and proves that this method is feasible.

aperture cavity；transmission line；reciprocal theorem；maximum induced current

TN79

A

1005－0388（2015）02－0328－05

顾长青（1958－），男，江苏人，南京航空航天大学教授，博士生导师，研究方向为电磁场数值算法、电磁兼容等.

王 斌（1991－），男，浙江人，南京航空航天大学硕士研究生，研究方向为电磁兼容.

李 茁（1979－），男，湖北人，南京航空航天大学副教授，博士，研究方向为电磁场数值算法、电磁兼容等.

顾长青，王 斌，李 茁，等.孔缝腔体内传输线负载上最大感应电流的研究［J］.电波科学学报，2015，30（2）：328－332.

10.13443／j.cjors.2014051501

GU Changqing，WANG Bin，LI Zhuo，et al.Analysis of the maximum induced current of transmission line in cavity with apertures［J］.Chinese Journal of Radio Science，2015，30（2）：328－332.（in Chinese）.doi：10.13443／j.cjors.2014051501

2014－05－15

国家自然科学基金青年基金（No.61102033）；中央高校基本科研业务费专项（NJ20140009）；江苏省高校优势学科建设工程资助项目

联系人：王斌E－mail：wangbinyq＠gmail.com