鱼雷贮存战备完好率主要维修性指标评估方法

董 琛

（海军装备部，山西省 侯马市 043003）

鱼雷贮存战备完好率主要维修性指标评估方法

董 琛

（海军装备部，山西省 侯马市 043003）

为了评估鱼雷的平均修复时间及维修度，在分析部队基层级维修保障活动的基础上，提出了采用结合验前信息的贝叶斯方法。通过具体的算例分析，证明该方法能够一定程度上将鱼雷的维修性水平直观地呈现出来，具有一定的可行性。

鱼雷 贝叶斯 平均修复时间 维修度

0 引言

平均修复时间作为鱼雷最核心的维修性参数，其指标成为衡量鱼雷维修性好坏的重要依据[1]；维修度是鱼雷贮存战备完好率中的重要参数，其指标表征故障雷在规定的任务准备时间内完成修复的概率[2]。两个指标的评估工作主要在鱼雷的设计定型阶段进行，根据试验得到的数据，通过统计计算，给出平均修复时间与维修度的指标评估值。

传统的方法是基于经典数理统计学的评估方法，在GJB2072-94《维修性试验与评定》中给出了两个指标的评估方法。平均修复时间的评估主要分为三种情况：维修时间服从对数正态分布时，维修时间对数均值和对数方差的估计；维修时间服从对数正态分布时，维修时间平均值和方差的估计；维修时间的分布未知时，维修时间平均值和方差的估计。维修度的评估存在两种情况：维修时间服从对数正态分布，维修时间的对数均值及对数方差未知；维修时间的分布未知。该方法虽然是较为成熟，应用广泛的方法，但由于需要样本量大，使得试验费用过高和时间过长，从而寻求新的小子样评估方法。

文献中曾出现运用贝叶斯方法对维修性指标进行研究，如文献[3]根据Bayes原理，结合验前信息，推导建立了小子样条件下修复时间为对数正态分布时的验证模型，并给出了试验所需样本量。也有运用SPOT方法对可靠性指标进行验证，如文献[4]给出了指数分布下可靠性指标截尾SPOT验证方法，文献[5]给出了二参数Weibull分布下可靠性指标SPOT验证方法。

在鱼雷研制、试验和调试等过程中，各功能组件或功能系统不可避免地会出现故障，对故障进行维修的历次信息，可以用于维修性指标的评估。通常获取的维修性观测信息，样本量较小，采用国军标的传统方法并不合适，本文针对对数正态分布下的鱼雷平均修复时间，使用结合验前信息的贝叶斯方法[6]对鱼雷平均修复时间及维修度进行评估。

1 基本假设与验前信息处理

1.1 基本假设

本文针对部队基层级维修中鱼雷的修复时间进行分析，主要进行的是故障LRU的换件维修，经历故障诊断、拆卸故障单元、更换故障单元、检验几个阶段，直至完成修复。其保障活动网络图如图1所示。其修复时间服从对数正态分布且方差已知，存在一定量的相关历史数据。

图2 维修保障活动网络图

1.2 验前信息处理

验前信息的获取一般包括三个途径：历史数据、仿真信息与专家经验。本文将借助历史数据对指标做出评估。在获得历史数据之后，首先通过科尔莫哥洛夫检验方法对其分布性进行检验，具体步骤如下：

STEP 1：假设修复时间X0服从对数正态分布，则Y=lnX～N(μ,σ2)。

STEP 2：根据获得的历史数据，估计出均值μ0与方差σ02。

由此便可得到F(X)=Y～N(μ,σ2)

STEP 3：根据下式计算最大偏差Dn。

STEP 4：对于给定置信度1-α，查K-S检验临界值表，得到临界值。如果Dn＜Dn,α，则接受假设，否则拒绝假设。

2 验后信息处理

2.1 一致性检验

经过试验得到小子样数据，需要对其和验前数据进行检验，判定是否属于同一分布，采用秩和检验法，具体步骤如下：

STEP 1：假设验前子样X0=(x1,x2,…,xn)，试验小子样X1=(xn+1,xn+2,…,xn+m)，假设两个子样来自同一分布。

STEP 2：将两个子样由小到大排序，可得次序统计量

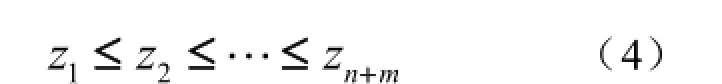
STEP 3：重新排序后，对于子样如果均不相等，则其秩即为统计量下标ri=i；如有子样相等，则其秩取统计量下表平均值。

STEP 4：将小子样X1=(xn+1,xn+2,…,xn+m)的秩和作为统计检验量。

STEP 5：对于给定的置信度1-α，查秩和检验表得到T的下限T1和T的上限T2。如果有T≤T1或T≥T2，则拒绝假设，否则接受假设。

2.2 确定验后分布

将修复时间的对数Y=lnX～N(μ,σ2)

作为研究对象。对于Y0，总体分布和方差σ2已知，验前样本均值μ0和方差σ02可由式（1）与式（2）得到，验前分布密度函数为：

由共轭分布法可知[7]，验后分布仍然服从正态分布Y=lnX～N(μ,σ2)，验后分布密度函数为：

利用Bayes方法可以求得n个试验数据时的均值1μ和方差21σ：

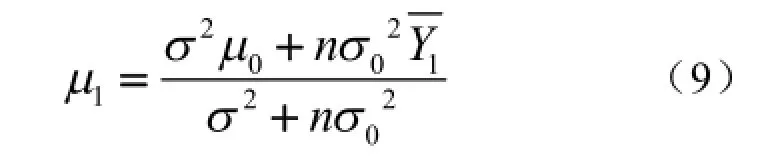
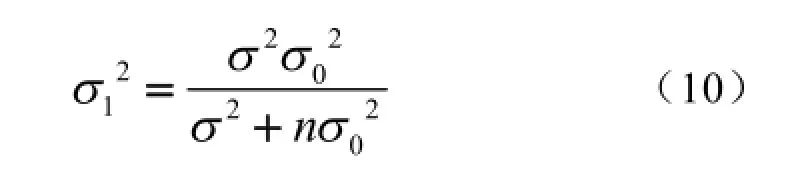
3 平均修复时间与维修度评估

3.1 平均修复时间

先对修复时间的对数做估计，再反推出平均修复时间的估计值。

最后进过反推即可得到平均修复时间的估计值。

3.2 维修度

维修度的估计是在平均修复时间估计基础上进行的，其点估计为：

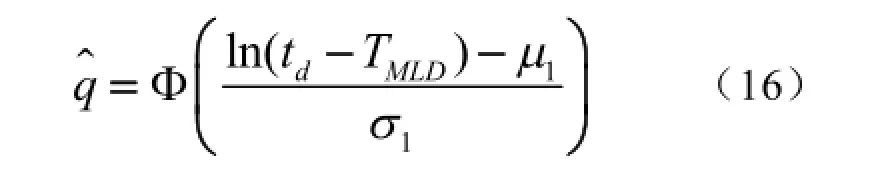
式中：dt从接到准备鱼雷指令到要求发往舰（潜）艇装载的间隔时间；MLDT为保障部队在其规定维修级别，为获取修复故障鱼雷所需保障资源的平均等待时间。

维修度的区间估计为：

置信度为1α-时，维修度的置信下限为：Zγ为标准正态分布的γ分位点。

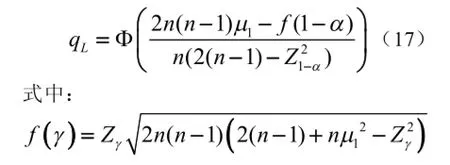
4 实例

某型鱼雷研制阶段现场试验小子样修复时间数据如表1所示。

表1 修复时间数据

于是，在置信度1α-为0.8的情况下，

5 结论

本文借助鱼雷在研制、试验和调试等过程中，各功能组件或功能系统出现故障时进行维修的历次信息，提出了在小子样情况下采用结合验前信息的贝叶斯方法，对设计定型阶段的鱼雷平均修复时间及维修度进行评估。借助该方法可以一定程度上将某型鱼雷的维修性水平直观地呈现出来。下一步可探讨部署使用阶段与鱼雷贮存战备完好率相关的主要维修性指标的评估方法。

[1] GJB2072-94维修性试验与评定[S]. 北京: 国防科学技术工业委员会, 1994.

[2] GJB451B鱼雷通用规范[S]. 北京: 国防科学技术工业委员会, 2012.

[3] 张金槐. 正态总体下分布参数的Bayes序贯估计[J].国防科技大学学报, 2002, (2): 95-100.

[4] 刘福成, 尚朝轩, 李刚. 小子样条件下电子装备维修性验证模型研究[J]. 现代电子技术, 2010, (21):3 8-40.

[5] 邢云燕, 武小悦. 指数分布下可靠性指标验证的SPOT截尾方法[J]. 系统工程与电子技术, 2006, (8): 1282-1284.

[6] 唐雪梅, 张金槐, 邵凤昌, 李荣. 武器装备小子样试验分析与评估[M]. 北京: 国防工业出版社, 2001.

[7] 王雪峥, 武小悦. 二参数Weibull分布下可靠性指标验证的SPOT方法[J].系统工程与电子技术, 2007, (6): 1009-1011.

Evaluation Method of Main Maintainability Indexes Related to Storage Operational Readiness Rate for Torpedo

Dong Chen
(Shanxi Military Representative Bureau of Navy Equipment Department, Houma 043003, Shanxi, China)

In order to evaluate mean time repair and maintenance probability for torpedo, based on the analysis of maintenance support activities at the grass-roots level in the army, Bayesian method combined with prior information is put forward. Through analysis of specific example, it shows out that maintainability for torpedo is visually presented to some extend through the method and the method might be feasible.

torpedo; Bayesian; mean time repair; maintenance probability

TJ63

A

1003-4862（2015）06-0028-03

2015-02-03

董琛（1988-），男，硕士，助理工程师。研究方向：武器系统运用与保障工程。