基于Snake模型的空间目标跟踪方法∗

许占伟12 王 歆12

(1中国科学院紫金山天文台南京210008)

(2中国科学院空间目标与碎片观测重点实验室南京210008)

基于Snake模型的空间目标跟踪方法∗

许占伟1,2†王 歆1,2‡

(1中国科学院紫金山天文台南京210008)

(2中国科学院空间目标与碎片观测重点实验室南京210008)

针对低轨变光空间目标和较亮空间目标的跟踪不稳问题,采用主动轮廓模型,提出一种改进的GVF-Snake算法,实现了星像实际轮廓的实时搜索.结合Kalman滤波外推,实现了一种空间目标的自适应跟踪方法.实验表明,跟踪过程中方法能够克服采用固定窗口带来的跟踪误差,提高跟踪的稳健性.

航天器,望远镜,技术:图像处理

1 引言

光学观测是空间目标监视的重要手段,空间目标的自动跟踪是空间目标监视的关键技术.跟踪的鲁棒性直接关系到空间目标的自动识别、定位和编目精度以及望远镜的运行效率.空间目标的自动跟踪是指在获取空间目标初始航迹后,根据实时采集结果外推跟踪位置,引导望远镜完成对空间目标的后续弧段的自动跟踪,跟踪过程包含了外推和实时采集两个不断重复的交互过程.

由于空间目标运动较快,采集帧频较高,对采集图像进行全图像处理耗费时间太长,因此多数采用在空间目标预测位置处开窗,以窗口质心作为目标质心.空间目标由于自身姿态调整或云层遮挡等原因,其视亮度会发生较大变化,在CCD图像上反映为其成像的大小变化.采用固定窗口时,成像大小的变化会使得窗口无法完全包含目标或者窗口内还有其他目标,从而导致窗口质心和目标质心偏差增大,严重时造成失跟[1].而对于极其明亮的目标,例如国际空间站等,在CCD图像上成像面积很大,固定窗口往往仅覆盖了成像中心区域的很小一部分,从而导致跟踪效果不佳.

文献[2-3]提出了根据成像大小自适应改变窗口大小的方法,一定程度上解决了由于目标成像尺寸变化带来的跟踪不稳问题,但若窗口中出现较强干扰时,窗口仍不能很好地包络住目标,影响跟踪效果.文献[4-5]将均值漂移(Meanshift)方法引入空间目标跟踪,可实现固定窗口的位置调整,但对于干扰造成的跟踪误差仍不能修正,只能丢弃采样,影响采集效率.

本文从主动轮廓模型出发,不使用固定的矩形窗口,而是搜索空间目标星像的实际轮廓.在改进GVF-Snake算法的基础上,和Kalman滤波相结合,形成了一种空间目标线性自适应跟踪方法,有效地解决了变光和成像较大空间目标的跟踪问题.

2 星像轮廓的获取

2.1 Snake模型

Snake模型是Kass等人为了跟踪人脸嘴部的轮廓于1988年提出的一种主动轮廓模型(active contour model)[6],由于其在图像噪声和图像对比度方面的卓越表现,并且其能很好地获得目标的封闭轮廓,在图像处理领域获得广泛的应用.Snake模型将目标轮廓作为一条连续的弹性曲线,并定义相应的能量函数,基于能量最小化准则进行曲线变形,从而使该弹性曲线向目标实际轮廓逼近,能量函数最小值处即为目标真实轮廓. Snake模型有效地将底层局部图像特征和目标外形轮廓线全局信息相互融合,从而实现图像的分割和识别.定义参数化轮廓线v的参数化方程为:

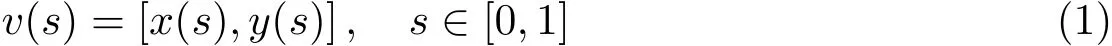
其中x和y是曲线在2维图像上的直角坐标,s是参数.在轮廓线上的能量函数为:

其中Etotal为总能量,Eint为内部能量,控制轮廓线的弹性形变,一般考虑曲线的连续性和刚性,定义为:

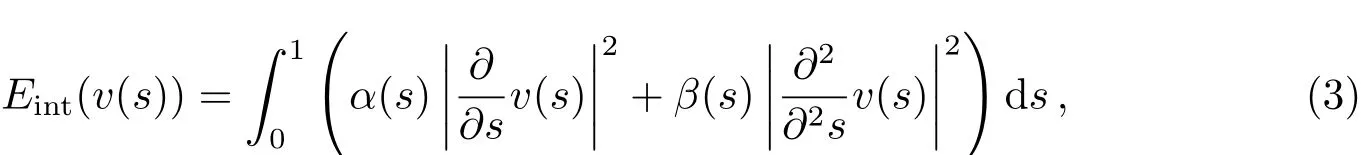
其中右边第1项为弹性能量,用于保持轮廓的连续性;第2项为弯曲能量,用于保持轮廓的光滑性.Eext为外部能量,一般考虑图像局部特征,如图像灰度、梯度变化等情况,定义为:

其中p(s)为图像势能函数.

从能量定义可见,弹性能量把轮廓曲线压缩成一个光滑的圆形,弯曲能量保持轮廓线光滑,外部能量趋使轮廓线向着感兴趣的图像特征处运动,正是在这3种力的共同作用下引导控制点趋向真实轮廓线边界.

2.2 离散化的Snake模型

在数字图像处理中,需要对上述算法进行离散化,离散化的轮廓线v由N个控制点构成,定义为:

则总能量函数为:

利用差分代替微分,有:

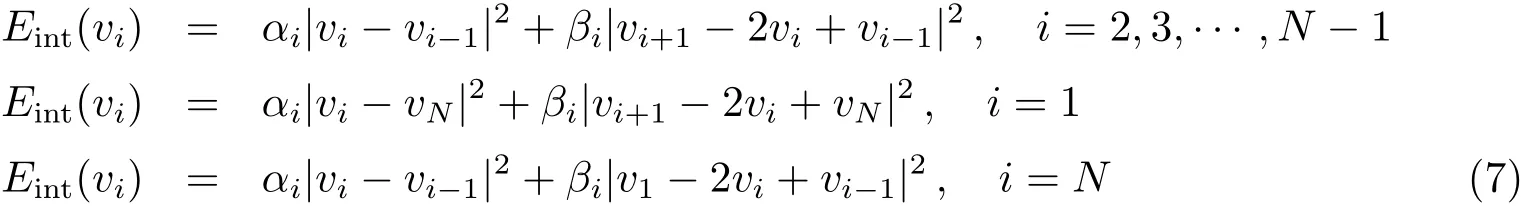
其中αi和βi为控制参数.

传统的Snake算法搜索范围小,无法捕获凹陷边界,而空间目标在跟踪过程中星像并不十分圆整,对于亮星常常出现凹陷边界,因此在外力选取上采用了梯度矢量流(Gradient Vector Flow,GVF)能量场[7].

其中I为所采集的数字图像,γi为控制参数.采用了GVF能量场的Snake模型被称为GVF-Snake方法.轮廓线为能量函数极小的曲线v:

2.3 改进的GVF-Snake方法

由于空间目标在运动过程中易受到较亮恒星干扰,或遇星团围绕,而恒星和空间目标在成像上并无明显特征区别,易导致轮廓收敛到恒星星像;或由于云层遮掩、空间目标姿态调整造成成像变化较大,像斑较小,初始轮廓线过大,导致影响收敛速度,从而影响跟踪的实时性.因此在GVF-Snake方法基础上新增了控制能量Econtrol加快收敛速度,同时避免收敛到其他星像上.以跟踪预测位置C=(xc,yc)为中心,Econtrol的离散形式为:

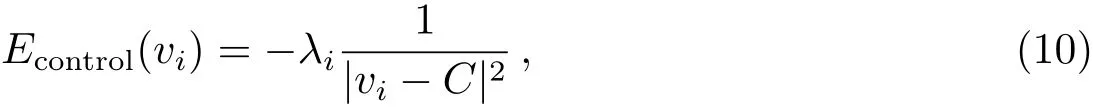
其中λi为控制参数,根据控制点所在位置改变轮廓线的搜索和膨胀,定义¯I为图像窗口的灰度均值,σ为灰度方差.当I(vi)＞+3σ时,认为控制点落入了星像中心附近,此时λi取负值,使得轮廓线快速向外扩张;当I(vi)＜+σ时,认为控制点落入了图像背景,此时λi取正值,使得轮廓线快速向内收缩;在其它区域时,控制点在轮廓线附近,此时取λi=0,利用图像梯度调整轮廓线.此外,控制力以预测位置为中心,这样可使轮廓线向预测位置附近收敛,避免收敛到干扰源.

在内力计算中,为了避免控制点集中到曲率较高的部分,对1阶导数进行修正[8]:

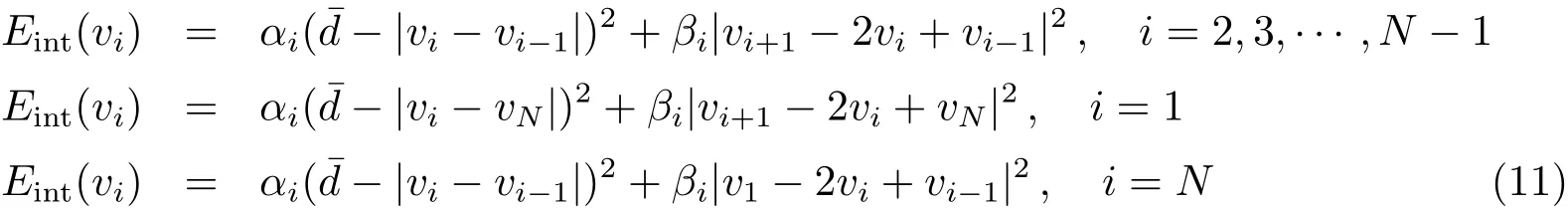
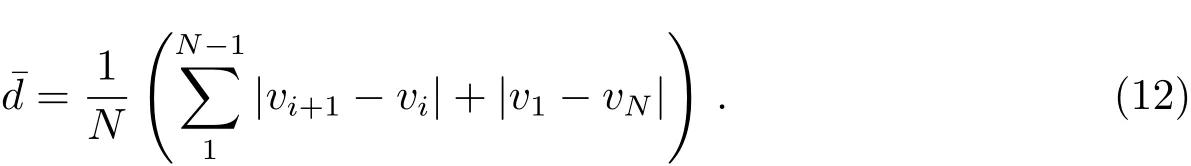
显然,1阶导数项上越接近各控制点平均距离值,其能量值越小,从而使各控制点能均匀分布于轮廓线上,避免控制点聚集.

改进后完整的Snake能量函数为:

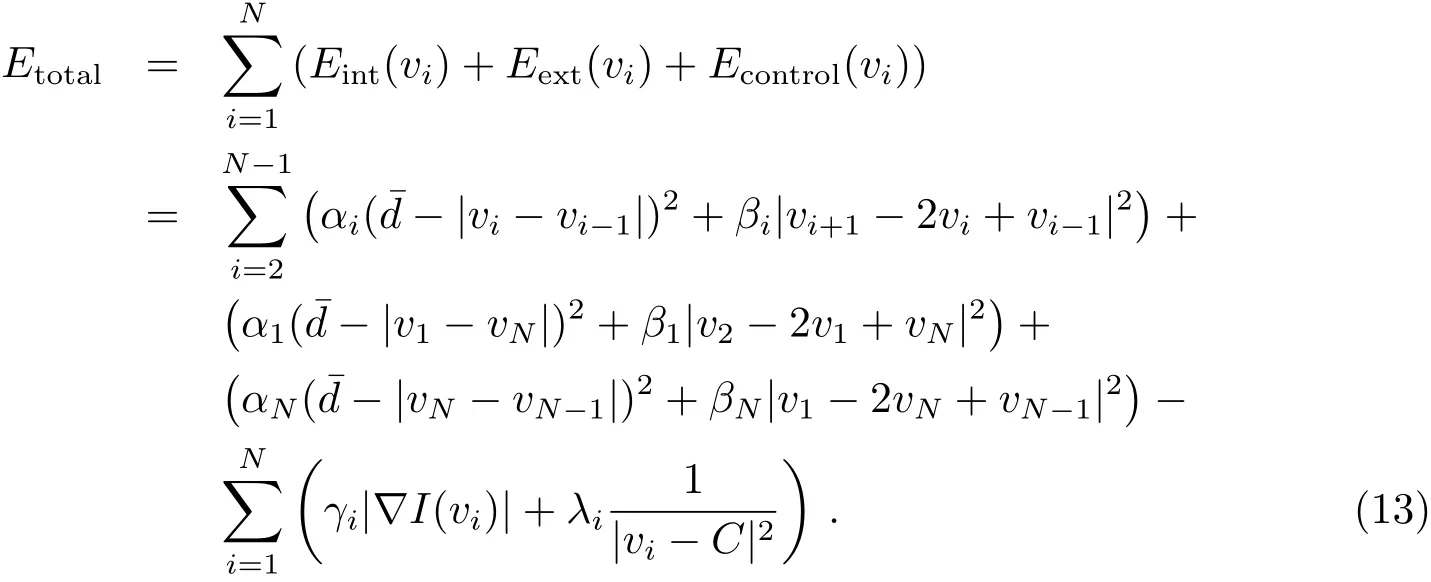
3 改进的空间目标跟踪算法

3.1 跟踪外推

空间目标的跟踪过程中需要根据当前时刻采集到的位置信息预测下一个时刻的位置,从而引导望远镜实现跟踪.Kalman滤波器是一种线性最小均方误差准则下的最优递归估计器,其在估计时不需要全部的历史数据,只需前一个输入信号和当前输入信号,非常便于空间目标的实时跟踪处理.因此我们仍通过Kalman滤波进行跟踪外推,采用和文献[4-5]一致的模型进行外推.

3.2 空间目标质心的计算

由于空间目标星像圆整度并不好,因此采用矩方法计算空间目标质心是最为广泛采用的方法[9].虽然通过Snake方法获取了空间目标实际轮廓,但求质心时严格按照轮廓计算耗费较多计算时间,仍采用矩形窗口求质心,选择轮廓线的外接矩形作为质心求取窗口.矩形中心(cx,cy)为:

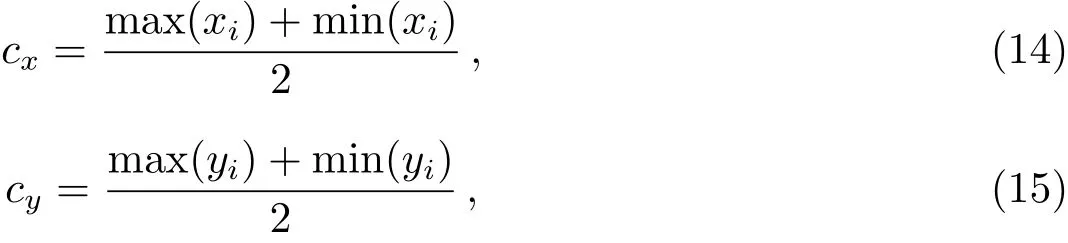
窗口的宽和高分别为:

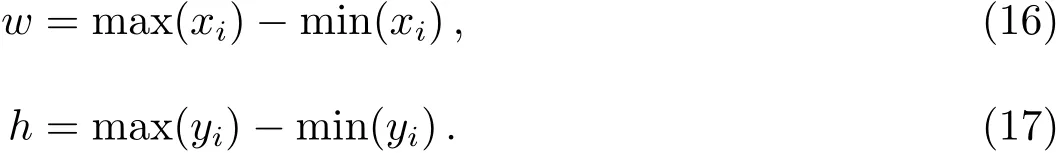
3.3 初始轮廓的选择和控制点调整

Snake算法需要给出一个初始轮廓,在跟踪过程中,以前一帧的轮廓作为下一帧的初始轮廓.空间目标成像远不及恒星规则,因此搜索到的轮廓形状相对复杂,如果以完整轮廓作为下一帧的初始轮廓,计算量增大同时效果并不显著.作为初始轮廓,对于星像而言,圆是一种合理的简化,这样轮廓只需要一个参数就可以表达,便于在跟踪过程中传递.定义轮廓的等效半径R为:

在跟踪过程中得到每帧最终轮廓后计算等效半径,在下一帧中以R为半径的圆作为初始轮廓.

另外,为了适应在跟踪过程中空间目标成像的尺寸变化,在轮廓搜索过程中避免控制点过密或者过稀,控制点数量也需要自适应地进行变化,采取下列措施增删控制点:若|vi+1−vi|＜/2,则删去点vi+1;若|vi+1−vi|＞2,则增加控制点v′=(vi+vi+1)/2.

3.4 跟踪过程

根据上述讨论,建立完整的基于改进GVF-Snake算法和Kalman滤波的跟踪过程,在获取初始航迹后,按如下具体步骤循环实施跟踪:

(1)引导望远镜到预测位置,采集一帧图像;

(2)在采集图像上以预测位置为圆心,前一帧得到的R为半径的圆周上平均选N个控制点作为初始轮廓;

(3)利用改进的GVF-Snake算法得到收敛的空间目标轮廓;

(4)根据收敛的轮廓计算外接矩形窗口,并获取空间目标质心;

(5)计算当前轮廓的等效半径;

(6)利用Kalman滤波更新数据,并外推下一个跟踪位置.重复步骤(1).

4 算法试验

为验证本文方法的有效性,使用中国科学院空间目标光学观测网中的40 cm口径的望远镜采集空间目标图像进行试验,图像分辨率为512×512 pixel,视场0.7°×0.7°.算法采用OpenCV库在VS2012平台上实现.试验中,弹性能量、刚性能量、外部能量权值皆采用定值,分别取值：αi=1.0,βi=0.5,γi=1.0,|λi|=3.0.轮廓搜索采用爬山法.

图1∼5分别给出了各种情况下的搜索结果,图中黑线为轮廓线,左边为初始轮廓,右边为搜索到的空间目标实际轮廓线.

图1为初始轮廓包含目标全部的情况,圆半径R=20 pixel,控制点数N=20,搜索时间4.973 ms.

图2为初始轮廓在目标内部的情况,圆半径R=8 pixel,控制点数N=20,搜索时间1.921 ms.

图3为初始轮廓包含目标大部分的情况,圆半径R=15 pixel,控制点数N=20,搜索时间5.451 ms.

图4为初始轮廓包含目标小部分的情况,圆半径R=15 pixel,控制点数N=20,搜索时间8.19 ms.

图1 初始轮廓包含目标的搜索结果Fig.1 The searching result with an initial contour surrounding the object

图2 初始轮廓在目标内部的搜索结果Fig.2 The searching result with an initial contour inside the object

图3 初始轮廓包含目标大部分的搜索结果Fig.3 The searching result with an initial contour containing the major part of the object

图4 初始轮廓包含目标小部分的搜索结果Fig.4 The searching result with an initial contour containing the minor part of the object

从上述结果可看出改进的GVF-Snake算法都能克服初始轮廓线取值偏差带来的困难,收敛的轮廓曲线能吻合空间目标实际轮廓线,计算速度能够满足空间目标跟踪帧频的需求.

为了验证算法抗干扰能力,图5给出了初始轮廓包含空间目标和干扰目标的情况,圆半径R=40 pixel,控制点数N=40,搜索时间30.928 ms.

图5 干扰情况下的轮廓搜索过程Fig.5 The contour searching process with an interference

在初始轮廓包含干扰目标的情况下,方法首先搜索到了两个目标的部分边界,但在控制能量的干预下克服了干扰目标的外部能量,迅速搜索到了所求目标的实际轮廓线.因此改进的GVF-Snake算法在初始轮廓偏差以及伴有较强干扰情况下,都能很好地达到预期目的.

最后为了验证跟踪整体效果,选择一颗变光空间目标进行了试验,该目标在运行过程中由于自身姿态变化会出现亮度突变.

图6给出了该目标连续的3帧图像,可见在第2帧目标突然变亮,星像溢出了固定窗口,而到第3帧时又突然变暗,恢复到第1帧时的亮度.

图6 变光目标的成像图序列Fig.6 The image sequence of an object with variational brightness

图7 给出了跟踪过程,其中粗线为每帧的初始轮廓.图中可见,第2帧时目标变亮,以第1帧收敛轮廓的等效圆作为初始轮廓,轮廓陷于目标内部,但最终轮廓膨胀收敛到了实际轮廓;第3帧目标亮度恢复正常,以第2帧结果作为参考的初始轮廓则远大于实际星像,最终收缩收敛到了实际轮廓,实现了自适应跟踪.

图7 变光目标的跟踪过程Fig.7 The tracking process of an object with variational brightness

5 结论

上述实验表明,本文提出的方法有效可行.通过引入主动轮廓模型,在空间目标跟踪过程中不再局限于固定窗口,而是能够搜索到目标的实际轮廓,在当前计算条件下搜索时间已能满足实时跟踪的需要.将Snake模型与Kalman滤波相结合,不仅仅能够适应光度变化目标以及较亮空间目标的跟踪,同时也适用于一般空间目标的跟踪,是一种稳健的空间目标自适应跟踪新方法.

[1]王科伟,马超杰,陈炜,等.应用光学,2009,30:353

[2]王莉,李忠海.沈阳航空工业学院学报,2009,26:38

[3]Zou W J,Bo Y M,Chen Y.Infrared and Laser Engineering,2008,37:602

[4]王歆,许占伟.天文学报,2012,53:145

[5]Wang X,Xu Z W.ChA&A,2012,36:426

[6]Kass M,Witkin A,Terzopoulous D.International Journal of Computer Vision,1988,1:321

[7]Xu C Y,Prince J L.ITIP,1998,7:359

[8]李熙莹,倪国强.光子学报,2002,31:606

[9]季凯帆,王锋.天文学报,1996,37:85

Space Object Tracking Method with Snake Model

XU Zhan-wei1,2WANG Xin1,2
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)
(2 Key Laboratory for Space Object and Debris Observation,Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)

Aimed at the unstable tracking problem of low-orbit variable and bright space objects,an active contour model is accepted,and a re fi ned GVF-Snake algorithm is proposed to realize the real-time searching of the real contour of objects on CCD image in this paper.Combined with the Kalman fi lter for prediction,a new adaptive tracking approach is proposed for space objects.Experiments show that the method can overcome the tracking difficulty brought by a fi xed window,and improve the tracking robustness.

space vehicles,telescopes,techniques:image processing

P123;

A

10.15940/j.cnki.0001-5245.2015.03.010

2014-11-04收到原稿

∗国家自然科学基金项目(11373072)资助†xzwei@pmo.ac.cn

‡wangxin@pmo.ac.cn