伽马射线暴的各向异性分布的特征∗

干力雄邹远川戴子高

(1华中科技大学物理学院武汉430074)

(2南京大学天文与空间科学学院南京210093)

伽马射线暴的各向异性分布的特征∗

干力雄1†邹远川1‡戴子高2#

(1华中科技大学物理学院武汉430074)

(2南京大学天文与空间科学学院南京210093)

从过去的威尔金森微波各向异性探测器(Wilkinson Microwave Anisotropy Probe)到现在的普朗克卫星(Planck satellite),宇宙微波背景辐射图的反常现象已经被广泛地认知.其中一个反常是:从l=2到l=5的多极矩存在耦合现象.为了考察伽马射线暴中是否存在与微波背景辐射相同的反常现象,研究了伽马射线暴的角分布.对伽玛暴样本的角分布进行球谐函数展开,得到前几项展开项的系数,发现从l=2到l=4有一定程度的耦合,而l=5与前面几个极矩相距较远.而且,四极矩分布是趋近平面化的,而其他几个极矩没有这样的特征.

伽马射线暴,宇宙学:宇宙背景辐射

1 引言

宇宙微波背景辐射是一种能够反映宇宙深层性质的观测现象.十年前,有人已经根据威尔金森微波各向异性探测器的数据研究发现了其异常[1].这种异常包括:宇宙微波背景辐射的四极矩较小,这种现象出现的概率为1/20;宇宙微波背景辐射的八极矩分布趋近平面化,这种现象的概率为1/20;四极矩和八极矩的方向存在耦合,这种现象出现概率只有1/60.随后,有更多的研究者参与到这个领域中[2−4].此外,研究表明从l=2到5的多极矩都高度耦合[5].最近,普朗克卫星提供了更加精确的宇宙微波背景辐射图,并且进一步确认其反常现象[6−7].直到现在,这些反常现象仍未得到合理解释.

除了微波背景辐射,在其他观测方面也发现了类似的现象.通过对类星体光谱的分析,人们发现了精细结构常数是各向异性分布的,并且存在较明显的偶极矩,其方向指向赤经(17.5±0.9)h、赤纬(−58±9)°[8].通过对超新星的分析,宇宙膨胀的加速度明显的方向位于(l,b)∼(130°,0°)[9−10].此外,研究者还利用伽玛暴来限定宇宙学参数[11−12].

在上述有趣现象的启发下,我们放眼于伽玛暴.与微波背景辐射不同,伽玛暴是宇宙中普遍而剧烈的现象,每天都能被探测到数个.伽玛暴在宇宙可观测物体中有着很高的红移,所以它们涵盖了宇宙中丰富的信息.其中一个有用的信息就是伽玛暴的角分布,这个课题已经被广泛研究了[13−18].一系列研究表明,短暴和中间暴呈各向异性分布,而长暴几乎各向同性.Tikhomirova等[19]提出了一个简单的方法来计算伽玛暴分布的四极矩,并且认为其很微小.

在这篇文章里,我们利用一种类似于分析微波背景辐射的方法(球谐函数展开)来分析伽玛暴的角分布,以获得展开项的前几项系数,再利用类似于de Oliveira-Costa等[1]的步骤来考察角分布是否也有异常.不同于微波背景辐射,伽玛暴的角分布可以考虑偶极矩的影响.在第2节,我们介绍了一种获得球谐函数展开系数的方法,并且模拟了一组包含特定分布模式的样本来检验这种方法.第3节,我们把第2节的方法应用到伽玛暴的样本上.第4节,我们做了分析和总结.

2 球谐函数展开

一个在球面上连续的函数可以利用球谐函数展开成如下形式,

其中

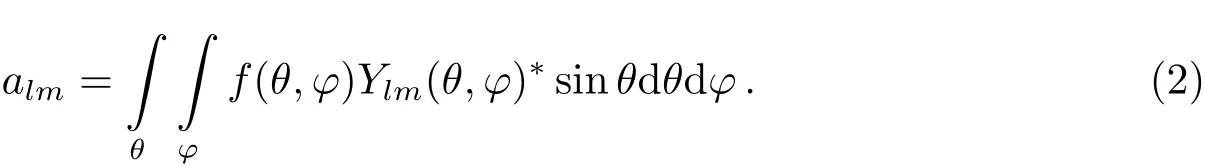
球谐函数如下归一正交:

上述方法只能用于展开连续的函数.然而,在实际问题处理中,我们经常要面对离散的函数分布.这里,我们使用一点小技巧来解决离散分布的问题.

在离散分布中,函数只在分离的多个点上有定义,所以我们不能用积分来获得球谐展开系数.而是把积分过渡为求和,

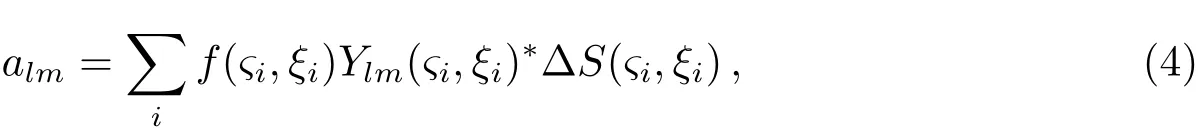
其中,我们采用了曲面参数域坐标(ςi,ξi),下标i表示不同面元中的不同坐标.∆S(ςi,ξi)是(ςi,ξi)所在的面元的面积.如果∆S(ςi,ξi)是无穷小,那么求和就等同于积分.接下来,我们认为f(ςi,ξi)等于伽玛暴在其对应的面元中的平均密度,

其中ni是伽玛暴在相应面元中的数量.既然划分球面的方式是任意的,所以我们能让∆S(ςi,ξi)变得任意小,以至于每个面元里只包含一个伽玛暴.这样,系数的表达式就能写成如下形式:

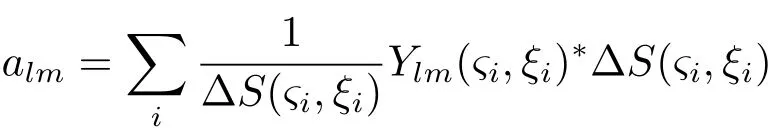
其中参数域坐标已经转化成了球坐标,下标i表示不同的伽玛暴.

我们结合上述的方法以及de Oliveira-Costa等[1]中的方法来寻找多极矩.首先,我们采用特殊的分布来检验我们的方法,也就是说,某种形似球谐函数Ylm(θ,φ)的方法.比如,如果一种分布完全等同于Y20,那么我们就会发现四极矩完全落在赤道面上.如果一种分布完全等同于Y33(θ,φ),那么我们会发现八极矩完全指向北极.

我们模拟了50000个点,这些点以Y20的模式均匀地分布在球面上.然后我们便得到了其离散的分布函数.使用上述方法,便得到了5个系数a2m,其中m=±2,±1,0.旋转这些系数寻找四极矩,最后得到其方向位于(θ,φ)∼(90°,232.5°),与期望一致.未旋转过和旋转过的系数实部罗列在表1.除了Y20(θ,φ),我们也能在正确的位置找到其他极矩的分布方向.

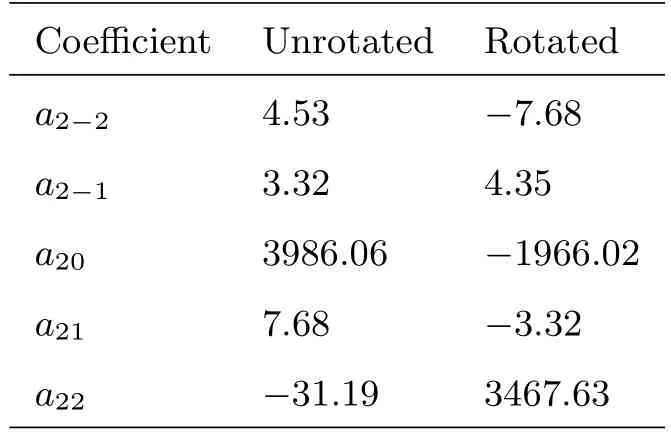
表1 未旋转过和旋转过的四极矩系数实部Table 1 The unrotated and rotated real-valued quadrupole coefficients

3 结果

利用上一节的方法,我们能够处理伽玛暴的角分布了.这里,我们采用了包含有3899个伽玛暴的样本,其中1236个伽玛暴来自http://www.mpe.mpg.de/˜jcg/grbgen. html(这个网页每天更新,选取的伽玛暴截止到GRB131014A.我们已经删除了包含在下面样本里的伽玛暴.)以及2 663个来自BATSE 4B样本[20](网址http://www.batse.msfc. nasa.gov/batse/grb/catalog/current/tables/basic table.txt).样本里的所有伽玛暴都采用了银道坐标.

在计算出我们想要的球谐函数展开系数后,我们马上得到了不同多极矩的特定方向,从nˆ1到nˆ5,如下:

转换到银道坐标,他们大致位于如下方向:

明显地,第2到第4个方向有一定程度上的耦合,而最后一个和第1个则在完全不同的方向上.图1展示了从l=1到l=5的多极矩分布图,其中深绿色表示正值,浅绿色表示负值.从偶极矩和四极矩图中,我们发现他们多极矩分布比其他几个图更加趋近于平面上,相应的方向垂直于该平面上(即深绿、浅绿相间的平面).图2表明了多极矩角动量在天球上的分布,其中较大的值用深蓝色表示.显然,在每张图中,多极矩方向的两端分别落在深蓝色区域里,深蓝色区域可以被认为是该方向的误差.

第2到第4个方向之间的夹角如下,

虽然这些夹角并不小,但是也不能完全被忽略,尤其是四极矩和八极矩之间的夹角.和微波背景辐射的多极矩方向作比较[1],

除了l=5,偶极矩也指向不同的方向,也与其他方向不耦合.偶极矩方向与另几个多极矩方向的夹角为

图1 l=1到l=5多极矩分布图.深绿色表示正值,浅绿色表示负值.Fig.1Distributions of multipole moments from the l=1 map to l=5 map.Deep green denotes positive values,and light green denotes negative ones.

图2 l=2和l=3的角动量分布图.深蓝色表示较大的值.Fig.2 Distributions of angular momentum dispersion in the spherical surface for l=2 and l=3,where larger values are in deeper blue

进一步,我们计算了统计参数tl,来描述每个多极矩趋近于平面的程度.tl的表达式为[1]

我们能发现偶极矩是明显平面化的.我们也能注意到四极矩也是较平面化.而其他几个多极矩没有这方面的反常.作为比较,微波背景辐射的八极矩的t等于94%[1].

4 讨论

采用3899个伽玛暴的角分布,我们计算得到了从l=1到l=5的多极矩的方向,并且发现了反常,即l=2,3,4的方向存在一定的耦合,夹角分别为θ23=13.6°,θ24= 28.2°,θ34=15.3°.而l=1和l=5的方向相距较远.伽玛暴分布的l=2,3,4多极矩虽然互相耦合,但是却没有与微波背景辐射的相应多极矩方向接近[1].而且,精细结构常数[8]和超新星[9−10]也存在某种特定的空间方向性,但是这些方向都没有相关联.

从论述中可以看出,我们的方法并不是很精确.我们展开伽玛暴分布的方法是一种近似的方法,这种近似会影响计算得到的系数.比如,在方程(5)中,我们采用了面元∆S(ςi,ξi)中的平均伽玛暴密度f(ςi,ξi)来替代面元中的伽玛暴个数,也就是说,我们把球面上的每个点赋予了一个值,这个值依赖于其附近的伽玛暴.因此,我们相当于把真实的伽玛暴分布转换成了另一种分布,该分布中球面上的每个点都有定义.我们不清楚这种转换对结果的影响,也不知道是否会影响多极矩的方向.

伽玛暴位置的误差也没有列入考虑范围.如我们所知的,许多伽玛暴没有确切的位置,有些伽玛暴的误差超过1°.因此,甚至真实的伽玛暴分布图也不如微波背景辐射图精确.另一个因素是伽玛暴数量不足.直到现在,上千个伽玛暴被探测到,与其他天体相比已经是个庞大的数量了.但是这仍然不够令人满意,因为球面上一共有40000多度,是伽玛暴数量的40多倍.这意味着,如果我们把每个伽玛暴放进一平方度的方格里,那么球面上就会有很多空的格子,所以分析伽玛暴的准确性就不那么让人信服.更糟糕的是,伽玛暴被多个仪器观测到,每个仪器有不同的阈值、轨道和视野,这些会导致选择效应.一种避免选择效应的方法就是我们可以考虑不同探测器所对应的子伽玛暴样本,去看看每一个子样本是否有相同的各向异性分布.然后,正如上面提到的那样,伽玛暴的不足使子样本的可信度变得很糟糕.所以,针对这些不确定性(比如位置误差和探测器的轨道覆盖范围),我们并不会进行子样本分析,除非伽玛暴的数量有了显著的增加.

最后,如果上文提到的误差影响足够小了,那么我们期待见到伽玛暴分布图和微波背景辐射图的潜在关联.这两个分布图分别来自不同的物理图像.微波背景辐射来自光子从最后散射面到观测者的传播,其各向异性来自于早期宇宙的涨落.另一方面,伽玛暴分布的各向异性可能来自于早期宇宙和随后的宇宙演化中产生的密度涨落.他们两者之间是否有关联并不明确.但是,如果我们的确发现了两者的联系,我们便获得了揭示早期宇宙结构的线索.

[1]de Oliveira-Costa A,Tegmark M,Zaldarriaga M,et al.PhRvD,2004,69:063516

[2]Copi C J,Huterer D,Schwarz D J,et al.MNRAS,2006,367:79

[3]Schwarz D J,Starkman G D,Huterer D,et al.PhRvL,2004,93:221301

[4]Ralston J P,Jain P.IJMPD,2004,13:1857

[5]Land K,Magueijo J.PhRvL,2005,95:071301

[6]Planck Collaboration,Ade P A R,Aghanim N,et al.A&A,2014,571:A1

[7]Planck Collaboration,Ade P A R,Aghanim N,et al.A&A,2014,571:A23

[8]Webb J K,King J A,Murphy M T,et al.PhRvL,2011,107:191101

[9]Cai R G,Tuo Z L.JCAP,2012,2:4

[10]Yang X,Wang F Y,Chu Z.MNRAS,2014,437:1840

[11]刘建炜,王发印.天文学报,2012,56:467

[12]Liu J W,Wang F Y.ChA&A,2012,36:155

[13]Balazs L G,Meszaros A,Horvath I.A&A,1998,339:1

[14]Cline D B,Matthey C,Otwinowski S.Gamma-ray Bursts in the Afterglow Era:Proceedings of the International Workshop.ed.Costa E,Frontera F,Hjorth J.Springer-Verlag,2001:56

[15]M´esz´aros A,Balazs L G,Bagoly Z,et al.AIPC,2009,1133:483

[16]M´esz´aros A,Bal´azs L G,Bagoly Z,et al.BaltA,2009,18:293

[17]Veres P,Bagoly Z,Horv´ath I,et al.AIPC,2010,1279:457

[18]Khabibullina M L,Verkhodanov O V,Sokolov V V.AstBu,2014,4:69

[19]Tikhomirova Y Y,Stern B E.AstL,2000,26:672

[20]Paciesas W S,Meegan C A,Pendleton G N,et al.ApJS,1999,122:465

The Signature of an Anisotropic Distribution of Gamma-ray Bursts

GAN Li-xiong1ZOU Yuan-chuan1DAI Zi-gao2
(1 School of Physics,Huazhong University of Science and Technology,Wuhan 430074)
(2 School of Astronomy and Space Science,Nanjing University,Nanjing 210093)

Anomalies of the cosmic microwave background(CMB)maps have been widely acquainted nowadays via the Wilkinson Microwave Anisotropy Probe(WMAP) satellite and the Planck satellite.One anomaly is a multipole alignment froml=2 tol=5.In our work,we investigate the angular distribution of gamma-ray bursts (GRBs)to fi nd whether there exists an anomaly similar to that of CMB.We perform a spherical harmonics expansion on the GRB samples to derive coefficients of a few multipole terms.A rough alignment froml=2 tol=4 exists,while thel=5 multipole points to a di ff erent direction.The quadrupole is obviously planar,while the other ones are normal.

gamma-ray bursts,cosmology:cosmic background radiation

P145;

A

10.15940/j.cnki.0001-5245.2015.03.002

2014-11-04收到原稿,2014-12-18收到修改稿

∗科技部973项目(2014CB845800)、国家自然科学基金项目(U1231101和11033002)资助†526407596@qq.com

‡zouyc@hust.edu.cn

#dzg@nju.edu.cn