基于一次差的灰色模型在卫星钟差预报中的应用∗

梁月吉12任 超12 杨秀发3 庞光锋12 蓝 岚12

(1桂林理工大学测绘地理信息学院桂林541004)

(2广西空间信息与测绘重点实验室桂林541004)

(3广西城市建设学校桂林541003)

基于一次差的灰色模型在卫星钟差预报中的应用∗

梁月吉1,2†任 超1,2 杨秀发3 庞光锋1,2 蓝 岚1,2

(1桂林理工大学测绘地理信息学院桂林541004)

(2广西空间信息与测绘重点实验室桂林541004)

(3广西城市建设学校桂林541003)

根据星载原子钟钟差的特点,提出一种基于一次差的灰色GM(1,1)钟差预报方法.该方法首先对相邻历元的钟差作一次差,然后以一次差后的值建立灰色模型预报一次差的值,最后将预报的一次差还原即得到钟差预报值.以IGS(International GNSS Service)提供的采样率为5min的精密钟差为实验数据,通过对不同长度的建模数据和不同预报步长进行对比分析.结果表明:该方法的预报精度较传统的灰色模型有了较大提高,特别是对于PRN01原子钟,其预报效果最好;采用一次差原理可有效改善和提高模型预报的精度和稳定性,应用于钟差较长时间预报是可行的,可靠性较强.

天体测量学:时间,方法:数据分析

1 引言

卫星钟差(satellite clock bias,SCB)的预报是一项非常重要的工作,钟差预报的可靠程度直接决定导航精度,研究钟差预报有利于提高参数预报的可靠性和准确性[1−3].目前,国内外许多学者已经研究出了多种预报方法,主要有:二次多项式模型、灰色模型、神经网络以及各种组合模型等[4−11].灰色模型具有所需样本数据少、抗干扰能力强等优点,通过对原始数据实行累加或累减使之成为具有较强规律的新数列,进而建立预报模型.由于星载原子钟相当敏感,极易受到外界或本身因素的影响,很难了解其细致的变化规律,可以把钟差的变化过程看作是灰色系统.为此,众多学者将灰色理论引入到钟差预报中研究,取得了比较好的成果:崔先强等[8]将灰色GM(1,1)应用到卫星钟差的预报中,通过使用已知的少数几个历元的卫星钟差来建模,减少了使用的数据量,提高了建模速度,而且使卫星钟差的预报精度得到显著提高;李玮等[9]将灰色系统模型应用于短期卫星钟差预报,预测精度比较高;路晓峰等[10]提出了灰色系统理论的优化方法并用于卫星钟差预报中,进一步提高预报精度;李晓宇等[11]提出一种改进灰色模型和ARMA (Auto-Regressive and Moving Average)模型的钟差组合预报模型,预测精度有了进一步提高.基于上述研究,本文结合钟差数据的特点、利用灰色系统的优良特性,提出了基于一次差的灰色GM(1,1)钟差预报方法.该方法首先对钟差相邻历元间作一次差,以一次差后的值作为灰色模型的建模数据建立预报模型,然后根据时间序列预报一次差的值,最后还原得到钟差预报值.本文以IGS提供的采样率为5 min的精密钟差数据为算例,探讨和研究对不同原子钟类型、不同建模数据以及不同预报长度的可行性和有效性.

2 基于一次差的灰色预测模型

根据原子钟的钟差数值可知,相邻历元的数值相差不大,对钟差序列相邻历元间作一次差,可得到有效数字位数减少的数据序列.设一组不同历元时刻的钟差值为:

对该序列相邻历元作一次差:

得到一组新的时间序列:

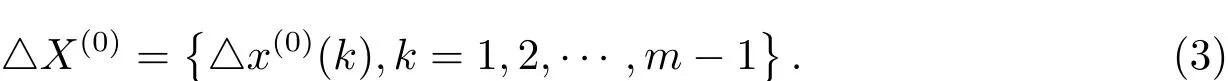
设△X(0)钟差序列对应的时间为tk(k=1,2,···,m−1),对其进行一次累加生成数列为:

建立相应的离散预测模型,利用样本的一次累加数列建立的预测模型如下[5−9]:

最后,通过将一次差预报序列和相应的钟差值对应相加便可得到所求历元的钟差,设预报的钟差序列长度为n,得出钟差预报表达式如下:

在建模前,必须检查原始数据序列正负号是否一致,若不是,则给每个元素都加上一个常数,而使该数列的符号一致.然后在此基础上建立灰色模型并进行预报,最后从预测值中减去常数c即可得到需要的预测结果.c的取值原则是:符号与原始数列中绝对值最大的数的符号一致,且其绝对值要大于原始数列中绝对值最大数的绝对值.

3 算例分析

由文献[12]可知,GPS在轨卫星的星载原子钟稳定性和精度由高到低依次为:Block IIR-M Rb钟、Block IIR Rb钟、Block IIA Rb钟和Block IIA Cs钟,其中Block IIA Cs钟的稳定性和精度相比其他类型的Rb钟低2∼3倍.且卫星钟差变化规律分为两种情况:一是呈单调递增或单调递减,二是呈非单调递增或递减,即钟差序列有递增也有递减.考虑到灰色模型的特性,同时为使实验更具代表性和一般性,本文选择4种类型钟所对应的一颗卫星进行实验,分别为PRN01、PRN04、PRN18和PRN31.以2013年7月1日至2013年7月3日IGS提供的精密钟差数据为实验数据,采样间隔为5min,即1h记录12个钟差历元,3 d共864个,如图1所示.可见,所选的4种类型原子钟的钟差均呈单调递增趋势,有利于建立GM(1,1)分析.

图1 卫星钟差序列Fig.1 The series of satellite clock bias

因此,利用传统的灰色GM(1,1)和本文方法对钟差预报过程进行分析,分别以前1∼24h钟差数据作为模型输入数据来建立模型,预报未来2、5、8、11、14、17、20、23、26、29、32和35h的钟差,即预报历元步长分别为24、60、96、132、168、204、240、276、312、348、384和420.由于使用的是IGS提供的精密钟差数据,其钟差序列自身误差很小,故以IGS相应的精密钟差值为基准,使用均方根误差(RMS)作为统计量,分析本文算法的有效性和可行性.4种类型原子钟差的一次差值如图2所示,各预报误差统计对比见图3∼6.限于篇幅,仅给出了基于一次差建模的不同建模数据及预报步长的预报结果统计表,见表1∼4.

图2 一次差序列Fig.2 The fi rst di ff erence series

由图3∼6可以看出,直接采用原始钟差数据建立GM(1,1)模型,预测不稳定,随着预报步长的增加,预报误差增大幅度较大;同时,随着建模数据的增加,预报精度也不一定随之提高.对原始钟差数据进行一次差后再建立灰色GM(1,1)模型,不同的建模数据和预报步长的预测精度均高于直接采用原始数据建模.由表1和表4可进一步看出,采用一次差建模,当建模数据达到一定长度后,对于较长时间的钟差预报,其预报精度均较为稳定;对于PRN01卫星钟差的预报,均方根大多小于0.05ns,优于PRN04、PRN18和PRN31卫星钟差的预报精度.结合图2分析发现,PRN01卫星钟差的一次差值波动性较为平缓,而PRN04、PRN18和PRN31卫星钟差的波动较为强烈,故其预报精度与卫星钟差的波动性存在一定的关系.可见,虽然GM(1,1)模型自身具有一定的抗干扰能力,但是由于钟差的有效位数过多,直接采用原始数据建模不利于模型预报,采用一次差对钟差数据预处理,对GM(1,1)起到较好的改善作用,当一次差值波动较小时, GM(1,1)模型具有更高的预报精度.综上,GM(1,1)的预报精度与稳定性不仅与预报步长有关,还与卫星钟类型及卫星钟差的波动性有关,不同的卫星钟预报表现出不同的特点.

为进一步验证本文模型对不同类型的原子钟钟差预报的有效性和可行性,分别建立以上4种原子钟的预报模型进行更深入分析,各模型预报过程与以上相同,限于篇幅,本文只给出最佳的预报结果.由以上分析可得出4种类型原子钟的一次差预报模型最佳输入数据分别为:PRN01以前6h钟差为建模数据;PRN04以前15h钟差为建模数据; PRN18以前21h钟差为建模数据;PRN31以前11h钟差为模型输入数据,各模型预报的钟差步长均为35h.各模型拟合和预报的误差如图7所示.

图3 PRN01不同预测步长对比Fig.3 The comparison of di ff erent prediction steps of PRN01

图4 PRN04不同预测步长对比Fig.4 The comparison of di ff erent prediction steps of PRN04

图5 PRN18不同预测步长对比Fig.5 The comparison of di ff erent prediction steps of PRN18

图6 PRN31不同预测步长对比Fig.6 The comparison of di ff erent prediction steps of PRN31

表1 PRN01一次差值预报精度统计表(单位:ns)Table 1 Statistics of prediction accuracies of PRN01’s fi rst di ff erence(unit:ns)

表2 PRN04一次差值预报精度统计表(单位:ns)Table 2 Statistics of prediction accuracies of PRN04’s fi rst di ff erence(unit:ns)

表3 PRN18一次差值预报精度统计表(单位:ns)Table 3 Statistics of prediction accuracies of PRN18’s fi rst di ff erence(unit:ns)

表4 PRN31一次差值预报精度统计表(单位:ns)Table 4 Statistics of prediction accuracies of PRN31’s fi rst di ff erence(unit:ns)

由图7(a)和(b)可知,直接采用原始数据建模,其拟合和预报误差均比较大,呈逐步上升趋势,对于PRN01和PRN04的最小预报残差为:−0.012ns和0.003ns,最大为:−0.811ns和3.985ns;对于PRN18和PRN31的预报残差最小为:−0.081ns和−0.010ns,最大达到:−2.187ns和−8.148ns.而使用一次差建模时明显改善和提高了灰色模型的稳定性和预报精度,PRN01的拟合和预报误差基本接近于0,PRN04的拟合和预报误差基本处于(−0.3ns,0.3ns)区间内,PRN18和PRN31的拟合和预报误差基本都在(−0.4ns, 0.4ns)区间波动.综上,基于一次差的灰色预报模型的预测效果较好,预报精度较高,特别是对PRN01原子钟差的预报效果明显优于预报其他原子钟差,且只需要较少的建模数据.

图7 4种类型的卫星钟差预报误差Fig.7 The prediction errors of the satellite clock bias for four types of clocks

4 结论

本文提出了基于一次差的灰色GM(1,1)钟差预报方法,经理论和算例分析,结果表明:使用灰色模型对卫星钟差序列进行预报,有效位数的多少对模型的预报性能有一定的影响;采用一次差原理对不同原子钟差进行预处理,使得灰色模型均能实现卫星钟差较高精度的预报,应用于较长时间的预报是可行的,同时简化了模型数据结构的复杂性; GM(1,1)的预报精度与稳定性不仅与预报步长有关,还与卫星钟差的波动性有关,采用一次差原理可有效提高模型预报的精度和稳定性.对灰色原理自身的缺陷做出进一步改进,再建立一次差预报模型,判断是否更适用于各种卫星原子钟差预报,同时针对不同类型的原子钟建立相应的预报性能更优的灰色模型是下一步需要深入研究的问题.

[1]Gotoh T.Improvement GPS time link in Asia with all in view.Frequency Control Symposium and Precise Time and Time Interval Systems and Applications Meeting,2005

[2]侯娟,董绍武,屈俐俐,等.天文学报,2012,53:319

[3]Hou J,Dong S W,Qu L L,et al.ChA&A,2013,37:90

[4]王国成,柳林涛,徐爱功,等.测绘学报,2014,43:803

[5]郭承军,滕云龙.天文学报,2010,51:395

[6]席超,蔡成林,李思敏,等.天文学报,2014,55:78

[7]Xi C,Cai C L,Li S M,et al.ChA&A,2014,38:342

[8]崔先强,焦文海.武汉大学学报:信息科学版,2005,30:447

[9]李玮,程鹏飞,秘金钟.测绘通报,2009:32

[10]路晓峰,杨志强,贾小林,等.武汉大学学报:信息科学版,2008,33:492

[11]李晓宇,杨洋,胡晓粉,等.大地测量与地球动力学,2013,33:59

[12]黄观文,张勤,王继刚.大地测量与地球动力学,2009,29:118

Grey Model Based on First Di ff erence in the Application of the Satellite Clock Bias Prediction

LIANG Yue-ji1,2REN Chao1,2YANG Xiu-fa3PANG Guang-feng1,2LAN Lan1,2
(1 College of Geomatics and Geoinformation,Guilin University of Technology,Guilin 541004)
(2 Guangxi Key Laboratory of Spatial Information and Geomatics,Guilin 541004)
(3 Guangxi City Construction School,Guilin 541003)

Considering the characteristics of satellite clock bias(SCB),a grey GM(1,1)model based on the fi rst di ff erence method is proposed.Firstly, fi rst di ff erence for two SCB values of adjacent epoch is derived to obtain the corresponding fi rst di ff erence sequences.Then,a grey model is made based on the sequences to predict fi rst di ff erence values of the following time series.Finally,the predicted sequences are recovered to the corresponding predicted SCB.The clock di ff erence data provided by the IGS(International GNSS Service)experiment are used to the experiment,and the cases with di ff erent lengths of data model and prediction step lengths are compared and analyzed.The result shows that prediction accuracy of this method is higher than that of the traditional grey GM(1,1)model,especially for the PRN01 satellite clock, whose forecast e ff ect is the best;With fi rst di ff erence,the model prediction accuracy and stability can be e ff ectively improved and enhanced.This method is feasible and reliable in the application of the relatively long time SCB prediction.

astrometry:time,methods:data analysis

P127;

A

10.15940/j.cnki.0001-5245.2015.03.007

2014-11-05收到原稿,2014-11-30收到修改稿

∗国家自然科学基金项目(41461089)、广西自然科学基金项目(2014GXNSFAA118288)、广西“八桂学者”岗位专项经费资助项目以及广西空间信息与测绘重点实验室课题(桂科能130511402、130511407)资助

†lyjayq@163.com