中子辐照量指数分布函数式中比例系数和平均中子辐照量的计算公式∗

张凤华周贵德 马 坤 马文娟 崔文元 张 波

(1沧州师范学院物理与信息工程学院沧州061001)

(2河北师范大学物理科学与信息工程学院石家庄050016)

中子辐照量指数分布函数式中比例系数和平均中子辐照量的计算公式∗

张凤华1,2†周贵德1马 坤1马文娟1崔文元2张 波2

(1沧州师范学院物理与信息工程学院沧州061001)

(2河北师范大学物理科学与信息工程学院石家庄050016)

已有的研究表明,在AGB(Asymptotic Giant Branch)星s-过程核合成模型发展演化的3个典型阶段中,其核合成区域中子辐照量分布在有效取值范围内都可视为指数分布,即ρAGB(τ)=C/τ0exp(−τ/τ0),但式中比例系数C和平均中子辐照量τ0的具体表达式相关文献中并未全部给定.通过深入剖析中子辐照量指数分布函数的基本求解方法,并系统梳理不同恒星模型中子辐照量分布函数的求解过程,得到了C和τ0的计算通式及其辅助关系式.只要确定了恒星模型中子辐照量的分立分布函数,就可以据此组公式确定出C和τ0与模型参量之间的关系式.所得结果有效地解决了利用解析方法求解目前流行的13C壳层(13C pocket)辐射燃烧AGB星s-过程核合成模型中子辐照量分布问题.

恒星:AGB和后AGB,恒星:中子,方法:解析

1 引言

s-过程即慢中子俘获过程,是为解释比铁族元素更重的元素(原子序数＞30)核合成而提出的一种物理机制[1].它要求较低的中子数密度条件(Nn＜108cm−3),使得任何不稳定的核都在俘获下一个中子前先进行衰变,s-过程路径沿β稳定谷.由于太阳系的重元素丰度分布的观测证据最详细、精确,因此在s-过程理论研究中常将其作为观测约束.

经典s-过程模型是研究中子俘获核合成的解析理论,是一种纯唯象的方法.经典模型指出,定义中子流NnvT(Nn为中子数密度,vT为中子的热运动速率)对时间的积分τ=∫NnvTdt,τ称为中子辐照量,表示在整个照射时间内通过单位面积的中子数目, Seeger等[2]和Clayton等[3]指出:若定义ρ(τ)dτ为中子辐照量在τ～τ+dτ的铁种子核数目(归一化到106个硅原子),ρ(τ)称为中子辐照量分布(以下简称DNE),则当唯象地取中子辐照量分布函数为指数衰减形式时,所得结果可以拟合太阳系的s-元素丰度分布,式中为太阳系中种子核56Fe的丰度,因子f为被中子照射过的56Fe核的比例,常数τ0称为平均中子辐照量.逐渐地,人们发现:要详细地解释全部的太阳系s-元素丰度分布至少需要3个不同的DNE,即弱分量(负责生产原子质量数A＜88的s-核素)、主要分量(生产88≤A≤208的s-核素)和强分量(生产约50%的208Pb)[4].1999年Arlandini等[5]给出拟合太阳系s-元素主要分量的τ0=(0.296±0.003)(kT/30)1/2mbarn−1,式中kT为以keV为单位的分子热运动能量.经典s-过程模型可确定s-过程的平均物理条件,如中子辐照量、中子数密度、温度以及s-过程时标等.对于单颗恒星的演化,平均中子辐照量的值依赖于恒星的金属丰度、质量和13C壳层的质量.

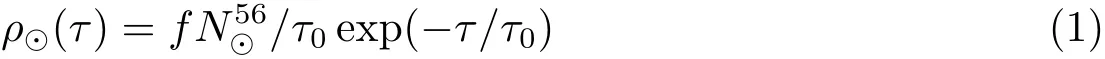
另一种研究s-过程的有效方法是进行与热脉冲AGB阶段的恒星模型耦合的核合成数值计算.AGB星是一个埋在巨大对流包层里的简并星,其核心收缩为具有通常白矮星大小的致密碳-氧简并核,在它的外面是双燃烧壳层–由内到外分别为氦燃烧壳层和氢燃烧壳层,在双燃烧壳层之间有一个很薄的、处于辐射平衡状态的、富氦的中间壳层,氢燃烧壳层外是对流的外包层.在AGB阶段的后期,恒星进入氦燃烧壳层热不稳定性而引发的热脉冲AGB阶段.一般说来,AGB星经历的脉冲数与其初始主序质量密切相关,如初始主序质量为1.3 M⊙的AGB星,热脉冲周期长达105yr,大约经历10～12个热脉冲后变为白矮星;而初始主序质量为5.0 M⊙的AGB星,热脉冲周期约为1000～3000 yr,可经历30～50个热脉冲才形成白矮星和行星状星云.在热脉冲循环进行的过程中,恒星将发生重要“第3次挖掘”现象(Third Dredge-up).在最后几个热脉冲过程中,恒星外包层会发生“星风质量损失”.AGB星模型的结构示意图如图1所示．

图1 热脉冲AGB星模型结构示意图,包括对流外包层的边界、氢燃烧壳层、氦燃烧壳层和氦中间壳层.介于氢壳层和对流包层边界之间的A区以及氦中间壳层内的B区,在第3次挖掘过程期间被混入到对流的包层[6].Fig.1 Illustration of the structure of a thermal pulse-asymptotic giant branch star,showing the border of the convective envelope,the H-burning shell,the He-burning shell,and the He intershell.The region A between the H shell and the border of the convective envelope and the region B in the He intershell are mixed into the convective envelope during TDU[6].

自从发现AGB星以来,大量天文观测数据显示,AGB星光球中的碳和重核素的丰度不同程度地高出一般恒星.根据AGB星外包层的碳、氧丰度比C/O,可将其分为两类:一类是C/O＜1的MS星和S星;另一类是C/O＞1的C星．1952年,Merrill[7]在天文观测中首次发现,在S星的光谱中包含有不稳定重核素99Tc(99Tc的半衰期是2×105yr),它的存在表明恒星内部正在发生重要的重元素核合成过程–s-过程以及核合成产物被混到恒星表面的过程．20世纪60年代中期通过对恒星演化图象的研究表明:热脉冲AGB星阶段的氦中间壳层是发生慢中子俘获最合适的场所[8−9].Cameron[10]等人在AGB星演化的He燃烧阶段引入了两个对重元素核合成至关重要的中子源:一个是13C中子源,通过反应13C(α,n)16O释放中子;另一个是22Ne中子源,通过22Ne(α,n)25Mg释放中子.其中,22Ne是由在H燃烧壳层中经过CNO循环合成的14N,在脉冲开始的早期,在He壳层中通过反应链14Ne(α,γ)18F(β+,ν)18O(α,γ)22Ne自然生成,而要形成一定量的13C,需要一个将质子混入He中间壳层的过程.

由于经典模型完全不依赖于恒星模型,因此能为恒星模型的核合成数值计算提供指导和约束,而恒星核合成区域的DNE就是联系两种方法的桥梁.原则上讲,相似的元素丰度分布应该对应相似的DNE,因此两种方法的研究结果应该是一致的.而事实上,在AGB星s-过程模型发展演化所经历的3个主要阶段中,上世纪70年代的热脉冲对流核合成模型[11](以下简称Ulrich模型,详见2.1节),以及80年代的13C壳层对流核合成模型[12−15](详见2.2节),都能在其核合成区域自然地给出指数形式的渐近DNE,即

式中r为连续经历两次热脉冲的物质占氦中间壳层的质量比例,称为重叠因子,Δτ为每次照射的中子辐照量.对于目前流行的第3代恒星s-过程核合成模型,即上世纪90年代中期建立起来的13C壳层辐射燃烧模型[16−18](详见2.3节),我们在文献[19-22]的研究表明,其渐近DNE虽然不再是严格的指数分布,但在中子辐照量的有效值范围内,仍可视为指数分布.文献[19-22]给出了对分立分布的DNE进行指数函数数值拟合确定τ0值的方法,显然这种方法不够简明准确,也不便于推广应用.τ0与模型参量的关系式是联系经典模型和恒星模型的桥梁,对研究两者的关系问题具有重要意义.因此,从解析理论推导角度探求τ0与该模型参量之间更直接、简明和准确的关系式是非常有必要的.

另外,由于

可见比例系数C表示达渐近分布时氦中间壳层内受中子辐照量照射的种子核数目比例,或说进入氦中间壳层内的新鲜物质受中子照射的概率.一般与不同模型对应的概率值不同,C的值在一定程度上反映了AGB星s-过程核合成模型的特点,因此准确确定C的值是很有意义的.对于对流核合成模型(包括Ulrich模型和13C壳层对流核合成模型),相关文献如文献[4,6,18,23]等并未给出C的具体表达式.对于13C壳层辐射燃烧核合成模型,文献[19-22]在确定C的取值时,只是仿照文献[18],将ρAGB(τ)归一到受中子照射过的物质比例,对于如何从理论上更合理地确定C的值未予讨论.

本文在对Ulrich模型DNE得出方法进行深入剖析的基础上,通过对不同AGB星模型DNE的得出过程进行系统的梳理,得到了中子辐照量指数分布函数式(2)式中平均中子辐照量τ0和比例系数C的计算通式及其辅助关系式.公式表明,只要确定了AGB星s-过程核合成模型中子辐照量的分立分布函数,就可以确定出τ0和C与模型参量之间的关系式.

2 AGB星s-过程核合成模型DNE指数函数表达式中比例系数和平均中子辐照量的确定

2.1 Ulrich模型

1973年,Ulrich[11]从TP-AGB模型出发,提出了一个具有重要意义的s-过程核合成模型,其主要特点是:(1)当对流的富He中间壳层的底部温度升高到0.8×108～0.9×108K时,13C中子源释放出中子,种子核经历中子辐照而合成新核素;(2)每个热脉冲对流氦中间壳层内所有物质(质量Msh)的中子照射情况都相同;(3)由于在热脉冲期间混合流将物质带到恒星表面以及在脉冲间隔期间4He燃烧生成13C导致氦壳层丢失质量,因此仅有质量为rMsh的物质可以连续经历两次热脉冲,其中比例系数r称为重叠因子; (4)在每个热脉冲开始时,都有(1−r)Msh的物质从外包层进入对流氦中间壳层区,它们含有没有经历过先前中子照射的种子核.假设Δτ为每个脉冲的中子辐照量,Ulrich列出了自第n个热脉冲进入的(1−r)Msh新鲜物质所经历的中子辐照情况,如表1所示.表中第1列标记脉冲的序数,第2列表示新鲜物质占氦中间壳层的质量比例,第3列表示所接受的中子辐照量,显然通式(1−r)rm(m=0,1,2···)即表示自任意第n个脉冲开始时进入的(1−r)Msh新鲜物质中,在第n+m个脉冲结束后仍能留在氦中间壳层且经历中子辐照量为(m+1)Δτ的物质比例.

表1 Ulrich模型自第n个热脉冲进入氦中间壳层区的(1−r)Msh新鲜物质的中子照射经历Table 1 The neutron irradiation history of the(1−r)Mshfresh matter which entered into the He intershell at pulsenin the Ulrich model

在此基础上，Ulrich给出了经过巨大数目的热脉冲后氦壳层内接受中子辐照量在τ附近单位区间内的种子核相对丰度

式中

f为从对流壳层混进外包层的质量占对流壳层的质量比例.后来的文献(如文献[4,6,18,23])中对方程(5)的引用方式一般为

其中τ0的表达式与(3)式相同.

为了更好地利用Ulrich模型的方法讨论其他类型AGB星s-过程模型的DNE,我们有必要对该方法做进一步的解读.

(1)如何从DNE的分立分布过渡到连续分布？

表1实际上给出了氦壳层达渐近分布(氦壳层内被先后进入的新鲜物质充满,即1−r+(1−r)r+(1−r)r2+···=1)时氦壳层内物质按中子辐照量的分立分布形式,即达渐近分布时氦壳层内中子辐照量为kΔτ(k表示新鲜物质受中子照射的次数)的物质比例为

对于如何从这个分立分布过渡到连续分布,Ulrich[11]实际上是假设氦壳层达渐近分布时, τ在0～Δτ之间的物质比例为P1=1−r,τ在Δτ～2Δτ之间的物质比例为P2=(1−r)r, ······,τ在(k−1)Δτ～kΔτ之间的物质比例为Pk=(1−r)rk−1,因此τ在τ～τ+Δτ之间的物质比例为(1−r)rτ/∆τ,而平均单位中子辐照量区间的物质比例为

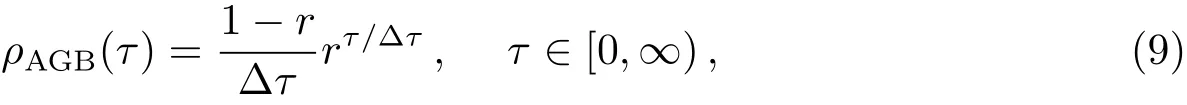
即得到了方程(5)中的第2个等式，也就得到了DNE的连续分布形式.可以看出中子辐照量的连续分布函数和分立分布函数有如下关系:

(2)如何确定DNE指数分布函数式(7)式中的平均中子辐照量和比例系数？

将(7)式写成等式,有

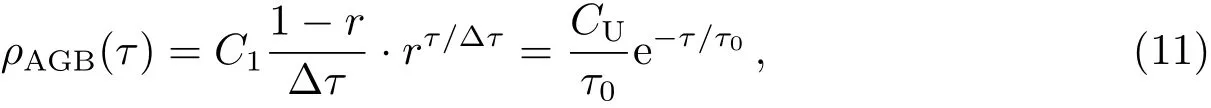
式中C1和CU为比例系数.对比(5)式和(11)式可知C1=1.而

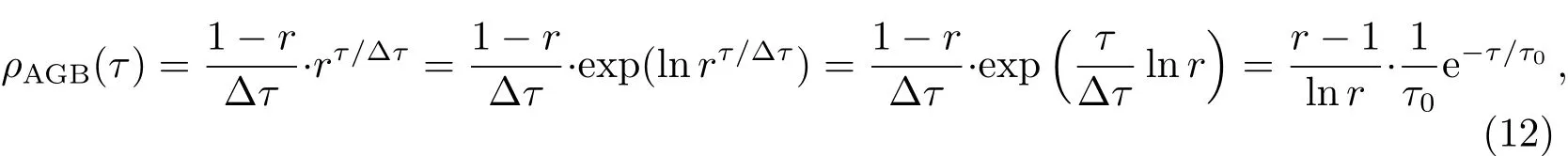
式中τ0的表达式与(3)式相同.对比(11)式和(12)式可知

(13)式就是由本文首次明确给出的比例系数CU的表达式．

2.2 13C壳层对流燃烧模型

1982年,Iben和Renzini[12−13]提出了一个适合于低金属丰度、低质量AGB星的13C壳层形成机制.80年代末90年代初,Hollowell等[14]和Kappeler等[15]在此基础上提出了一个包含两个中子源的低质量AGB星s-过程核合成模型,其基础假设是:在每个热脉冲过去之后,氦中间壳层顶部会形成一个13C密度随深度下降的13C薄层,该薄层保持不变,直到被随后到来的热脉冲吞并后在对流环境下通过13C(α,n)16O反应产生居主要地位的中子照射,种子核俘获中子形成新核素.当氦壳层对流至最充分时,底部的温度升高到约为3×108K,22Ne源刚能被激发,释放出中子数密度峰值较大的小量中子,种子核继续俘获中子合成新核素.这些产物最终在第3次挖掘中被混合到大气包层.文献[6,18]指出,这个模型虽然包含了两个中子源,但仍给出指数形式的DNE,即

其中τ0的表达式与(3)式相同.我们将上式写成等式

式中C2和CC皆为比例系数。

下面我们仿照Ulrich模型的方法来确定(15)式中比例系数CC.该模型是假设在每个对流热脉冲结束时有(1−r)Msh的新鲜物质进入氦中间壳层区,并在整个区内混合均匀,其中的(1−r)rMsh部分能够经历下一个热脉冲并接受期间的中子照射.仿照表1,我们在表2中列出了自第n个热脉冲进入的(1−r)Msh新鲜物质所接受的中子辐照量随所经历脉冲数的变化情况.

表2 13C壳层对流燃烧模型自第n个热脉冲进入氦中间壳层的(1−r)Msh新鲜物质的中子照射经历Table 2 The neutron irradiation history of the(1−r)Mshfresh matter which entered into the He intershell at pulsenin the13C-pocket convective burning model

由此可以得到氦中间壳层内DNE达渐近分布时壳层内物质按中子辐照量的分立分布形式，即氦中间壳层内中子辐照量为kΔτ的物质比例为

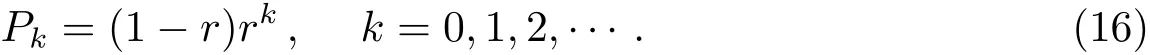
假设τ在0～Δτ之间的物质比例为P1=(1−r)r,τ在Δτ～2Δτ之间的物质比例为P2=(1−r)r2,······,τ在(k−1)Δτ～kΔτ之间的物质比例为Pk=(1−r)rk,k=1,2···,则中子辐照量τ在τ～τ+Δτ之间的物质比例为(1−r)r(τ+∆τ)/∆τ,而平均单位中子辐照量区间的物质比例为

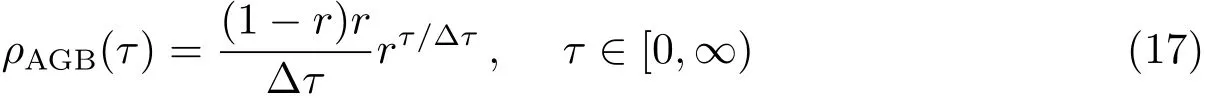
对比(15)式和(17)式,可知C2=1.而

式中τ0的表达式与(3)式相同.对比(15)式和(18)式可知

2.3 13C壳层辐射燃烧模型

20世纪90年代中期,Straniero等[16−17]提出了13C壳层辐射燃烧模型,Gallino等[18]对该模型给予了彻底的阐述.该模型表明,13C实际上是在热脉冲间隔阶段的辐射平衡状态下燃烧释放中子,13C壳层内的中子数密度以及由此产生的中子辐照量随着位置所处深度的增加而减小,壳层内的种子核随即俘获中子合成重元素.在下一个对流热脉冲到来时,该壳层区域的物质同氦中间壳层区未经历过该次s-过程的物质混合均匀,并接受来自22Ne源中子数密度峰值高但中子辐照量小的中子照射,在热脉冲结束时,又与来自外包层的新鲜物质混合均匀,之后经历下一个热脉冲循环.

我们在讨论该模型的DNE时,同文献[18]一样,不考虑13C壳层区中子辐照量随位置的变化以及模型参量随脉冲数的变化,且只考虑13C中子源的中子照射.需要指出的是, Busso等[24]曾指出,由于核合成区域(即13C壳层)很小,仅约占氦中间壳层质量的1/20,核合成产物在整个氦中间壳层的均匀混合使得不同核合成区域的生产因子逐渐非常接近.特别是最近的研究表明[25−26],只有采用13C均匀分布的13C壳层,才能拟合主族前太阳系碳化硅颗粒中的锆和钡同位素丰度.因此假设处于13C壳层区中子辐照量均匀分布是合理的,也是有必要的.在上述简化条件下,该模型是假设在某个对流热脉冲结束时自外包层进入氦中间壳层的质量为(1−r)Msh新鲜物质,其中的(1−r)rMsh部分可经历随后的热脉冲,但只有位于13C壳层区域的(1−r)qMsh(q表示13C壳层占对流氦中间壳层的质量比例)部分可以在两个脉冲间隔之间的辐射平衡状态下经历中子照射,其余(1−r)(r−q)Msh部分不被照射.假设种子核经历一次照射获得的中子辐照量都为Δτ,我们在图2中列出了自第n个热脉冲进入氦中间壳层的(1−r)Msh新鲜物质的中子照射经历分叉结构示意图.

将图2中所有τ=kΔτ的质量比例数相加,即可得到第n+m次脉冲结束时氦壳层内自第n到第n+m次脉冲先后进入的新鲜物质中接受中子辐照量为τ=kΔτ的质量比例.

文献[19-20]给出:

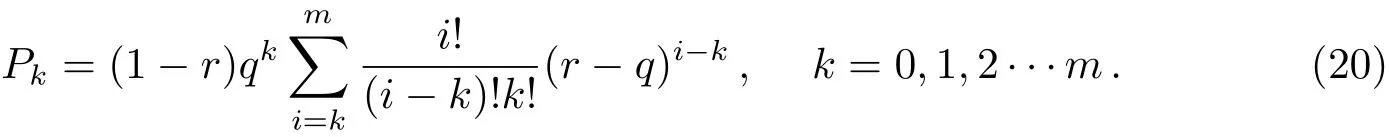
通过考察P(kΔτ)−τ曲线,文献[19-20]指出,此模型的渐近DNE在中子辐照量的有效取值范围内非常逼近于指数分布,因此仍可用指数分布函数来拟合,即

下面我们仿照Ulrich模型方法来求解上式中τ0和比例系数Cr的表达式．

对(20)式进行指数拟合,有

也就是说,

或

式中y只与r−q有关,P0等于图2中m→∞时中子辐照量τ=0的各项之和,即

仿照Ulrich模型的方法,将中子辐照量的分立分布函数(24)式转化成连续分布,有

或

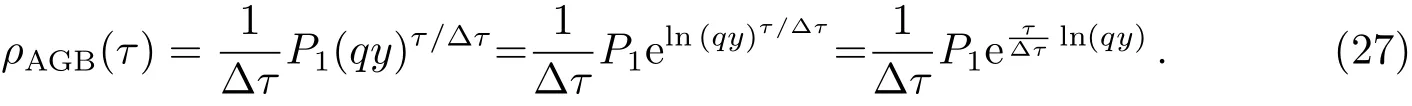
定义

有

可见,

为了得到y的表达式,我们进一步考察以上所讨论的各种模型的DNE．

一方面有:

Ulrich模型

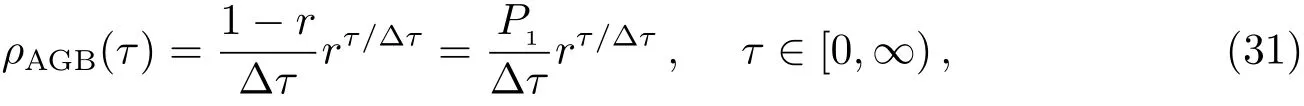
13C壳层对流燃烧模型

13C壳层辐射燃烧模型

考虑到在对流s-过程核合成模型中,种子核经历热脉冲即经历中子照射,因此可以认为,在(31)～(32)式中,rτ/∆τ中的重叠因子r在此处表示种子核连续经历两次中子照射的概率,因此类似地,(33)式中的qy也是这个含义,不妨称其为准重叠因子.

另一方面,Ulrich模型中,新鲜物质都是自各次脉冲开始时进入,都至少经历一次中子照射,所以新鲜种子核受中子照射的概率pU为1,此概率也可以通过计算DNE达渐近分布时氦中间壳层内受中子照射(即至少经历一次照射)的物质比例Ptotal求得,即

但13C壳层模型(包括13C壳层对流燃烧模型和13C壳层辐射燃烧模型)中,(1−r)Msh新鲜物质是自脉冲结束时进入氦中间壳层,只有(1−r)rMsh的物质能经历下一次热脉冲,并全部(13C壳层对流燃烧模型)或部分(13C壳层辐射燃烧模型)地经历中子照射,因此新鲜种子核受中子照射的概率小于1.此概率仍然可以通过计算渐近分布时氦中间壳层内受中子照射的物质比例Ptotal求得．

对于13C壳层对流燃烧模型,新鲜种子核受中子照射的概率

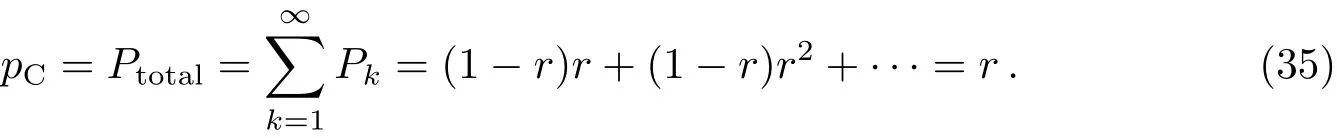
可以看出,pC正好等于种子核连续经历两次照射的概率r．

对于13C壳层辐射燃烧模型,如果把(33)式中的qy看成是准重叠因子,表示种子核连续经历两次照射的概率,则该模型就与13C壳层对流燃烧模型有完全类似的结构.因此类似地,qy也就应该等于该模型新鲜种子核受中子照射的概率(用pr表示).考虑到Ptotal等于图2中除τ=0的各项之和，则应有

因而

(37)式是通过类比方法得到的结果,是否正确还需验证．

由(22)式知

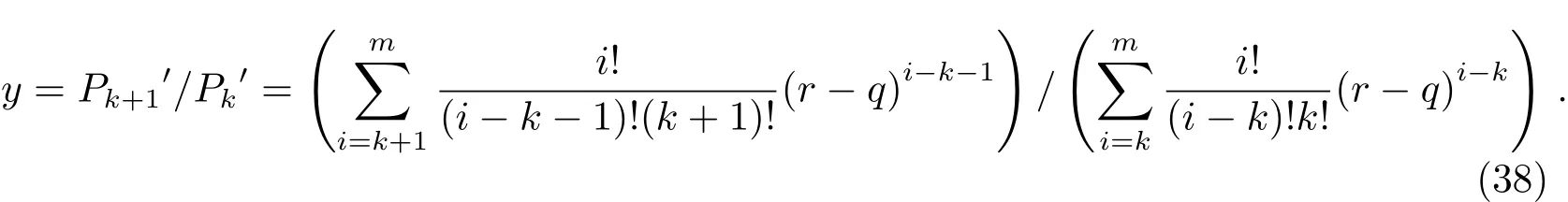
我们将假设的r−q的一些可能取值分别代入(37)式和(38)式中,得到了完全相同的y值，如表3所示.这充分证明了(36)式或(37)式的正确性.

表3 对(37)式的验证Table 3 The veri fi cation of Eq.(37)

将(24)、(25)及(36)式的结果代入(30)式,得到

将(36)式代入(28)式,得到

为了表明公式与模型的对应关系,在(40)式中将平均中子辐照量用τ0r表示．

3 AGB星s-过程模型中子辐照量指数分布函数式中比例系数C和平均中子辐照量τ0的计算通式

根据第2节的讨论,我们可以归纳总结出AGB星s-过程模型DNE指数分布函数(2)式中比例系数C和平均中子辐照量τ0的计算通式及其辅助关系式,即:若已知AGB星s-过程模型DNE的分立分布函数,即DNE达渐近分布时氦中间壳层内经历任意k(k= 0,1,2···)次照射的物质比例Pk,则

式中R表示进入氦中间壳层的新鲜物质能连续经历两次中子照射的概率.其中,对于对流核合成模型(包括Ulrich模型和13C壳层对流燃烧模型),

对于13C壳层辐射燃烧模型,

我们称(43)～(44)式为通式(41)～(42)式的辅助关系式．

以上结论的得出是基于基本简化假设条件:模型参量不随脉冲数变化,且脉冲数可以有足够多个,使核合成区域的DNE达渐近分布.事实上,对于条件更加复杂的AGB星s-过程核合成模型,通式(41)～(42)式也是适用的.例如,目前仍在被深入探讨的13C壳层辐射燃烧的低质量AGB星s-过程模型[25−33],其重叠因子、对流氦中间壳层的质量、13C壳层质量等模型参量都随脉冲数变化.并且由于只有发生第3次挖掘的热脉冲才会形成13C壳层,进而使种子核受到中子照射发生s-过程核合成,因此在讨论氦中间壳层区域的DNE时,只能考虑带挖掘的脉冲(假设为kmax个),所得分布也不是渐近分布,我们不妨称其为最终分布.文献[21-22]给出了考虑模型参量q、r随脉冲数变化但各次照射的中子辐照量Δτ都相同时氦中间壳层区域分立形式的DNE,即DNE达最终分布时氦中间壳层内接受任意k(k=0,1,2···)次中子照射的物质比例的表达式.文献[21-22]的计算结果表明,在中子辐照量的有效值范围内,最终DNE分布仍然可以用指数函数式(2)式来拟合.此时模型的qy的值是随脉冲数变化的,若引入平均准重叠因子的概念,并合理认为其值等于DNE达最终分布时氦中间壳层内受中子照射的物质比例,则我们仍然可以利用(41)～(42)式来确定该模型DNE指数拟合函数式中的平均种子辐照量(用表示)和比例系数(用表示),只需取

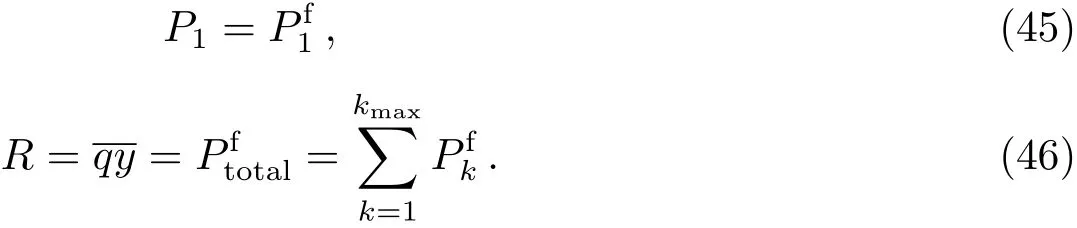
4 结果和讨论

本文在深入剖析Ulrich模型指数形式DNE得出方法的基础上,通过对不同AGB星s-过程核合成模型DNE的求解过程进行系统的梳理,给出了不考虑模型参量随脉冲数变化时三代AGB星s-过程核合成模型DNE指数拟合函数式(2)式中比例系数C和平均中子辐照量τ0的具体表达式,即(13)、(19)、(39)～(40)式,并进一步归纳总结出了C和τ0的计算通式(41)～(42)式以及辅助关系式(43)～(44)式;在此基础上,将通式的应用范围拓展到任意复杂条件的13C壳层辐射燃烧的AGB星s-过程模型,给出了辅助关系式(45)～(46)式,得到了13C壳层辐射燃烧模型C和τ0的普适计算公式.研究结果表明:只要确定了AGB星s-过程模型DNE的分立分布函数,就可以由通式和辅助关系式确定出DNE指数分布函数式(2)式中C和τ0与模型参量之间的关系式.

为了检验上述所得公式的可靠性,我们仿照文献[18]的图8,取重叠因子r=0.45,壳层的质量比例q=0.05,每次中子照射的辐照量Δτ=0.2 mbarn−1.事实上这组模型参量值可以认为是13C壳层辐射燃烧模型参量的典型值或平均值:因为按照文献[18],一个标准13C壳层的质量比例约为0.05,且在分子热运动能量kT=8 keV时,对于3 M⊙、太阳金属丰度的AGB星模型,一个标准13C壳层一次照射产生的中子辐照量平均值为0.2 mbarn−1,而该模型重叠因子的渐近值r=0.45.我们首先将这组模型参量值分别代入(3)、(13)及(19)式，得到τ0=0.25 mbarn−1,CU=0.688,CC=0.310,相应的Ulrich模型和13C壳层对流燃烧模型的DNE分别如图3曲线1和2所示.可以看出,计算结果与文献[18]的图8一致.再将上述模型参量的取值分别代入(39)和(40)式,得到Cr= 0.0305,τ0r=0.08 mbarn−1,所得τ0r值与文献[19-20]所得τ0=0.08 mbarn−1一致,相应的13C壳层辐射燃烧模型的DNE如图3曲线3所示.另外,文献[21-22]计算了考虑模型参量随脉冲数变化时上述3 M⊙、太阳金属丰度的13C壳层辐射燃烧模型分立形式的DNE,据此可以得到R==0.0664,=0.0625,将其代入(41)和(42)式得=0.0230,=0.074 mbarn−1,所得值与文献[21-22]的计算结果τ0=0.073 mbarn−1一致,相应的DNE如图3曲线4所示.需要强调的是,文献[19-22]τ0的计算式是通过对中子辐照量分立分布计算结果进行指数函数数值拟合得到的,而本文τ0的计算公式是利用解析方法推导出来的,所表示的τ0与模型参量的关系更加直接、简明和准确,便于推广应用,而准重叠因子概念的引入也使得公式的物理含义更加明确.本文计算结果与文献[18]及[19-22]计算结果的一致性,充分证明了本文所得C和τ0计算公式的可靠性.

图3 不同AGB星s-过程核合成模型的中子辐照量分布Fig.3 The distributions of neutron exposures predicted from di ff erent AGB star models for the s-process nucleosynthesis

本文研究结果是非常有意义的,主要体现在以下几个方面:

(1)C和τ0的计算通式揭示了三代AGB星s-过程核合成模型内在的统一性,而三代模型的C和τ0不同的具体表达式,又反映出不同模型各自的具体特点.因此,利用这些公式,结合恒星模型的核合成数值计算结果,能使我们更好地理解和把握AGB星s-过程核合成模型演化和发展的趋势．

(2)在s-过程理论的研究发展过程中,经典模型与恒星模型两种方法的关系是一个重要的理论问题.在Ulrich模型、13C壳层对流燃烧模型阶段,由于两种模型能在核合成区域自然地给出指数形式的DNE,因此恒星模型方法和经典模型方法是一致的,并且通过关系式(3)式,经典模型为恒星模型的核合成数值计算提供指导和约束[4,6].然而,目前流行的13C壳层辐射燃烧的低质量AGB星s-过程模型,其DNE变得非常复杂,难以做解析表述,使得该模型与经典模型的关系也一直没有得到充分的阐述和论证.本文总结出的C和τ0的计算通式,在揭示三代AGB星s-过程核合成模型存在内在一致性的同时,也间接证明了13C壳层辐射燃烧模型与经典模型的一致性.而本文给出的13C壳层辐射燃烧模型C和τ0的计算公式,则彻底解决了利用解析方法求解该模型DNE的问题,为广泛探讨不同质量和金属丰度下该模型DNE的特点,充分论证该模型与经典模型的关系问题提供了强有力工具.

(3)13C壳层辐射燃烧的低质量AGB星s-过程模型仍然是目前被深入探讨的恒星模型[25−33].由于13C壳层的形成机制仍未确定[30],因此在拟合恒星观测丰度的核合成计算中,13C壳层质量(对应模型参量q)、13C总量(对应模型参量Δτ)以及13C分布常被作为自由参量,有时也被观测结果约束[25−26].因此,利用本文给出的13C壳层辐射燃烧模型DNE指数函数式中C和τ0与模型参量q、r和Δτ之间的关系式,探讨经典模型对该恒星模型核合成数值计算的指导和约束作用是一个很有现实意义的研究课题.

[1]Burbidge E M,Berbidge G R,Fowler W A,et al.RvMP,1957,29:547

[2]Seeger P A,Fowler W A,Clayton D D．ApJS,1965,11:121

[3]Clayton D D,Ward R A.ApJ,1974,193:397

[4]K¨appeler F,Beer H,Wisshak K.RPPh,1989,52:945

[5]Arlandini C,Kappeler F,Wisshak K,et al.ApJ,1999,525:886

[6]Busso M,Gallino R,Wasserburg G J.ARA&A,1999,37:239

[7]Merrill P W.Sci,1952,115:484

[8]Schwarzschild M,H¨arm R.ApJ,1967,150:961

[9]Sanders R H.ApJ,1967,150:971

[10]Cameron A G W.ApJ,1955,121:144

[11]Ulrich R K.The s-process in Stars//Schramm D N,Arnett W D.Explosive Nucleosynthesis.Austin: University of Texas Press,1973:139-167

[12]Iben I Jr,Renzini A.ApJ,1982,249:L79

[13]Iben I Jr,Renzini A.ApJ,1982,263:L23

[14]Hollowell D,Iben I Jr.ApJ,1988,333:L25

[15]Kappeler F,Gallino R,Busso M,et al.ApJ,1990,354:630

[16]Straniero O,Gallino R,Busso M,et al.ApJ,1995,440:L85

[17]Straniero O,ChieffiA,Limongi M,et al.ApJ,1997,478:332

[18]Gallino R,Arlandini C,Busso M,et al.ApJ,1998,497:388

[19]张凤华,周贵德,张波.天文学报,2008,49:133

[20]Zhang F H,Zhou G D,Zhang B.ChA&A,2008,32:369

[21]张凤华,周贵德,崔文元,等．天文学报,2013,54:9

[22]Zhang F H,Zhou G D,Cui W Y,et al．ChA&A,2013,37:405

[23]Cristallo S.PASP,2006,118:1360

[24]Busso M,Gallino R,Lambert D L,et al.ApJ,2001,557:802

[25]Liu N,Savina M R,Davis A M,et al.ApJ,2014,786:66

[26]Liu N,Gallino R,Bisterzo S,et al.ApJ,2014,788:163

[27]K¨appeler F,Gallino R,Bisterzo S,et al.RvMP,2011,83:157

[28]Cristallo S,Piersanti L,Straniero O,et al.ApJS,2011,197:17

[29]Bisterzo S,Gallino R,Straniero O,et al.MNRAS,2012,422:849

[30]Cristallo S,Di Leva A,Imbriani G,et al．A&A,2014,570:46

[31]Bisterzo S,Travaglio C,Gallino R,et al.ApJ,2014,787:10

[32]Cristallo S,Abia C,Straniero O,et al.ApJ,2015,801:53

[33]Liu N,Savina M R,Gallino R,et al.ApJ,2015,803:12

Calculating Formulas of Coefficient and Mean Neutron Exposure in the Exponential Expression of Neutron Exposure Distribution

ZHANG Feng-hua1,2ZHOU Gui-de1MA Kun1MA Wen-juan1CUI Wen-yuan2ZHANG Bo2
(1 Department of Physics and Information Engineering,Cangzhou Normal College,Cangzhou 061001)
(2 College of Physics Science and Information Engineering,Hebei Normal University, Shijiazhuang 050016)

stars:AGB and post-AGB,stars:neutron,methods:analytical

P144;

A

10.15940/j.cnki.0001-5245.2015.06.004

2015-03-11收到原稿,2015-05-23收到修改稿

∗国家自然科学基金项目(11273011、U1231119)、河北省自然科学基金项目(A2014110008、A2011205102)资助

†zfh1968zfh@163.com