NTSC守时氢钟性能分析∗

宋会杰123 董绍武12 王正明12 屈俐俐12 景月娟123李 玮12

(1中国科学院国家授时中心西安710600)

(2中国科学院时间频率基准重点实验室西安710600)

(3中国科学院大学北京100049)

NTSC守时氢钟性能分析∗

宋会杰1,2,3†董绍武1,2 王正明1,2 屈俐俐1,2 景月娟1,2,3李 玮1,2

(1中国科学院国家授时中心西安710600)

(2中国科学院时间频率基准重点实验室西安710600)

(3中国科学院大学北京100049)

首先对NTSC(National Time Service Center)守时实验室的氢原子钟进行了测试,为了规避铯原子钟噪声较大的影响,没有采用TA(k)或UTC(k)作为参考,而是以4台氢原子钟互为参考进行测试,利用四角帽法对氢原子钟的频率稳定度进行分析,估计出单台氢原子钟在不同取样时间上的Allan标准差.然后根据氢原子钟的特性,扣除趋势项,剔除异常值,利用数学方法平滑,分离出了氢原子钟的高斯噪声,并且通过了Kolmogorov-Smirnov检验,估计出单台氢原子钟高斯噪声.

天体测量学,时间,方法:统计

1 引言

守时实验室负责产生一个国家或者地区的时间和频率的基准[1],时间保持的质量或精度很大程度上取决于守时系统的构成:(1)原子钟、(2)主钟系统、(3)原子时算法、(4)主钟频率驾驭算法等[2],每一部分都存在着一定的噪声或误差[3],影响着守时系统产生时频基准信号的质量.目前,国际上大国和主要发达国家都十分重视时间噪声和误差的研究和投入,达到提高守时精度的目的.

随着2014年BIPM(BUREAU INTERNATIONAL DES POIDS ET MESURES)改变了原子时算法,氢原子钟的权重大幅度提高,其地位愈显重要.与此同时,国际上主要的时间实验室多数采用氢原子钟作为主钟.与国际相比,NTSC的守时实验室的氢原子钟数量较少且运行超过10 yr(2台,代号为H226和H227),且采用铯原子钟作为主钟,虽然守时水平依然保持在国际先进行列,但是为了紧跟国际守时发展趋势,NTSC新引进2台氢原子钟(代号为H296和H297),以期为NTSC的本地原子时TA(k)的计算和主钟驾驭奠定技术基础.

新引进的氢原子钟短期稳定度超过了铯原子钟,有可能超过以前的两台氢原子钟,在没有高一级参考标准的情况下,如何对这两台氢原子钟性能进行测试评估是一项较难的工作.

原子钟作为守时工作的核心,输出脉冲信号和频率信号,传统的分析方法就是通过计算其Allan偏差分析频率稳定度指标,也就是主要分析原子钟的5种基本噪声[4].为了更全面了解氢原子钟噪声的高斯分布情况,本文结合Vondrak平滑法和Kolmogorov-Smirnov检验法分离出高斯噪声,并给出了Allan偏差估计,更全面地了解了氢原子钟的性能.

2 Allan方差估计

2.1 Allan方差的定义[5]

Allan方差定义的特点是利用计算差分序列的方法,差分以后的序列是平稳的,其方差就不随取样数变化.如果已知的值的两个样本连续值之间没有停滞时间,则它的两个方差样本平均半值就等于Allan方差,于是有

其中xi为时差序列.利用可以求得

(1)式和(2)式使频率稳定度具有时域特征.

同样,由谱密度可以转化成Allan方差,我们有

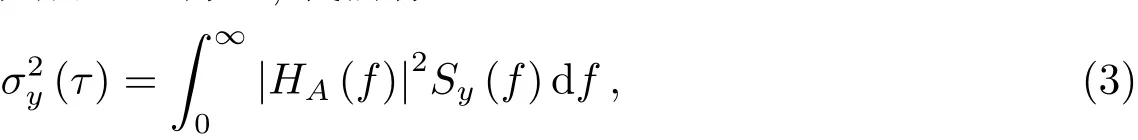
这里Sy为频率谱密度函数,|HA(f)|2为转换函数模的平方.它代表频域中与Allan方差计算相联系的数学滤波,转换函数为

当f→0时,|HA(f)|2随f2变化,这样可以保证在下限时对所有的α值进行积分.α代表噪声类型.

2.2 多角帽法估计[6]

对于3台钟的情况,根据(5)式,则应有

这种估计方法可以推广到M台钟的情况(M＞3),则

上式在时频工作中称为多角帽法.

2.3 数据分析

从2014年7月1日0时至10月31日0时,4台氢钟的相位差比对曲线见图1.分别对6条氢钟两两比对曲线计算不同步长下的Allan偏差(AD),表1计算出了4台氢原子钟通过相互比对的Allan偏差估计.利用相互比对数据计算得到的Allan偏差估计,通过四角帽法解得4台氢原子钟不同取样时间下的Allan偏差估计如表2.图2是4台氢钟部分比对(扣除了二次多项式之后)的相位差曲线.

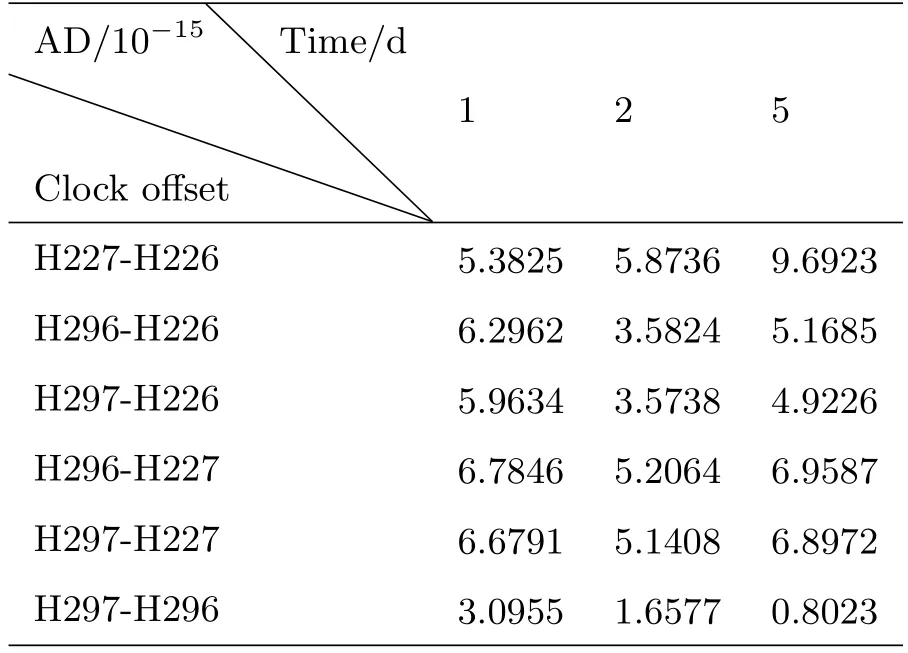
表1 氢钟两两比对的Allan偏差Table 1 The Allan deviations of hydrogen masers comparing with each other

表2 氢原子钟的Allan偏差估计值Table 2 The Allan deviation estimations of hydrogen masers

分析图2,两台新到的氢钟的比对曲线H297-H296在扣除了二次多项式之后(为叙述方便起见下面不再赘述“在扣除了二次多项式之后”)的变化比其他3条曲线的变化平缓(说明两者的频率比较稳定):H227-H226(两台2004年购的氢钟)曲线有很大的变化幅度.查看另外两条曲线可知H227-H226的大幅度变化应该是H227较大的频率波动引起的.分析表1和表2,氢原子钟H297和H296的1 d、2 d和5 d的频率稳定度优于H226和H227,H297对于不同取样时间的频率稳定度优于H296,说明对于以上取样时间,H297的频率稳定度最高.H226对于不同取样时间的频率稳定度优于H227,H227相应取样时间的频率稳定度最差.

3 氢原子钟的高斯噪声估计

高斯噪声是一种随机噪声,表示任取n个样本值,其值服从高斯分布(正态分布).高斯噪声衡量原子钟符合高斯分布的噪声情况,其大小仍用Allan偏差进行估计,也可作为衡量原子钟性能的一个重要指标.同上述分析,利用原子钟的比对数据,得出氢原子钟H226、H227、H296、H297的两两比对结果,然后分别扣除比对结果的二次多项式, 4台氢原子钟的相互比对结果见图3.利用Vondrak平滑法对扣除比对结果的二次多项式的残差数据进行平滑处理.

3.1 Vondrak平滑原理[7]

设有时间引数为ti的测量资料xi(i=1,2,...,N).Vondrak方法平滑测量数据的基本原理是

其中

3.2 Kolmogorov-Smirnov检验[8]

平滑后的残差数据利用3σ法则进行异常值的去除,并做正态分布检验,选用非参数Kolmogorov-Smirnov检验,检验原理为:当样本容量n很大时,经验分布Fn(x)是总体分布函数F(x)的很好近似.所用定理为:设总体的分布函数F(x)连续,则当H0: F(x)=F0(x)为真时,有

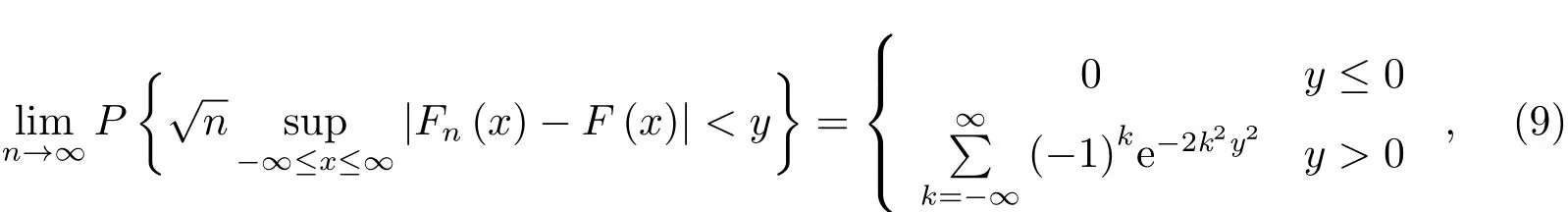
选取统计量

对于给定的水平α,由附表查得临界值Dn,α,使得

对样本观测值(x1,x2,···,xn)T,计算统计量Dn得观测值.如果,则拒绝H0(F(x)=F0(x)),否则接受H0.

3.3 数据分析

分别对3σ法则进行异常值去除后的残差数据做正态检验,直到通过检验,否则继续进行3σ法则去除异常值.通过正态分布检验的分布密度图如图4所示.

平滑后的残差数据进行异常值剔除后通过正态检验,认为是氢原子钟本身的高斯噪声,得到的Allan偏差如表3所示.利用最小二乘原理估计平滑后各台氢原子钟高斯噪声的Allan偏差估计值如表4所示.

图3 4台氢钟两两比对(扣除了二次多项式之后)的相位差曲线Fig.3 Phase di ff erence curves of four hydrogen masers after deducting quadratic polynomial comparing with each other

表3 氢原子钟相互比对的高斯噪声的Allan偏差Table 3 The Allan deviations of hydrogen masers’Gaussian noise comparing with each other

表4 氢原子钟的高斯噪声的Allan偏差Table 4 The Allan deviations of hydrogen masers’Gaussian noise

分析图3、图4、表3和表4可知:氢原子钟不同取样时间的高斯噪声水平不同,对于每台氢原子钟,取样时间取为1 d、2 d、5 d,随着取样时间的增加,高斯噪声的Allan偏差变小,其中取样时间为5 d的Allan偏差最小.

图4 平滑数据的残差分布图Fig.4 The distribution diagram of smooth data residuals

对于不同氢原子钟相同的取样时间的高斯噪声水平差异也明显,其中氢原子钟H297在相应的取样时间表现出的Allan偏差最低,氢原子钟H227在相应的取样时间表现出的Allan偏差最大.

结合前面分析的氢原子钟的频率稳定度,氢原子钟的频率稳定度与高斯噪声水平有一定相关性,频率稳定度高的氢原子钟,表现出高斯噪声的Allan偏差也小.

4 结论和讨论

基于Allan方差和多角帽法估计出单台氢原子钟的不同取样时间的Allan偏差,能够评定出相应取样时间的氢原子钟的频率稳定度.为了更进一步了解各台氢原子钟的性能,文中采用Vondrak平滑方法并结合了非参数Kolmogorov-Smirnov检验的方法分离出高斯噪声,并估计出各台氢原子钟不同取样时间的高斯噪声的Allan偏差,为守时工作提供支持.

文中得出氢原子钟在不同取样时间的Allan偏差估计与相应高斯噪声估计的Allan偏差具有一致性.比如氢原子钟H297在不同取样时间的Allan偏差最小,相应的H297在不同取样时间的高斯噪声的Allan偏差也最小,分析结果具有一致性.

另一方面,对氢原子钟高斯噪声的分析为氢原子钟的噪声阈值设定和设备异常情况的检测提供了重要的参考.

[1]董绍武.守时中的若干重大技术问题研究.西安:中国科学院国家授时中心，2007

[2]Allan D W,Weiss M A,Jespersen J L.A Frequency-domain View of Time Domain Characterization of Clocks and Time and Frequency Distribution System.IEEE Frequency Control Symposium,1991: 667-677

[3]Peil S,Hanssen J,Swanson T B.Performance and Applications of an Ensemble of Atomic Fountains. PTTI Precise Time and Time Interval Systems and Application Meeting,2012:269-271

[4]卫国.中国科学(A辑),1992:80

[5]Cyganowski C J,Whitney B A,Holden E,et al.AJ,2008,136:2391

[6]卫国.陕西天文台台刊,1990,13:2

[7]丁月蓉,郑大伟.天文测量数据的处理方法.南京：南京大学出版社,1990

[8]师义民,徐伟,秦超英,等.数理统计.北京：科学出版社,2008

Analysis of NTSC’s Timekeeping Hydrogen Masers

SONG Hui-jie1,2,3DONG Shao-wu1,2WANG Zheng-ming1,2QU Li-li1,2JING Yue-juan1,2,3LI Wei1,2
(1 National Time Service Center,Chinese Academy of Sciences,Xi’an 710600)
(2 Key Laboratory of Time and Frequency Primary Standards,National Time Service Center,Chinese Academy of Sciences,Xi’an 710600)
(3 University of Chinese Academy of Sciences,Beijing 100049)

In this article,the hydrogen masers were tested in NTSC(National Time Service Center)keeping time laboratory.In order to avoid the impact of larger noise of caesium atomic clocks,TA(k)or UTC(k)was not used as reference,and four hydrogen masers were mutually referred and tested.The frequency stabilities of hydrogen masers were analyzed by using four-cornered hat method,and the Allan standard deviation of single hydrogen maser was estimated in di ff erent sampling time.Then according to the characteristics of hydrogen masers,by removing the trend term,excluding outliers, and smoothing data with mathematical methods to separate the Gaussian noise of hydrogen masers,and fi nally through the normal Kolmogorov-Smirnov test,a single hydrogen maser’s Gaussian noise has been estimated.

astrometry,time,methods:statistical

P127;

A

10.15940/j.cnki.0001-5245.2015.06.008

2015-03-20收到原稿,2015-06-04收到修改稿∗国家自然科学基金项目(11473029)资助

†songhuijie@ntsc.ac.cn