大质量中子星PSR J0348+0432原生星的组成与结构∗

洪 斌 贾焕玉母雪玲 周 霞

(西南交通大学现代物理研究所成都610031)

大质量中子星PSR J0348+0432原生星的组成与结构∗

洪 斌 贾焕玉†母雪玲 周 霞

(西南交通大学现代物理研究所成都610031)

在相对论平均场理论中考虑重子八重态,选取每重子熵S=1或S=2,集中研究讨论了熵效应对大质量中子星PSR J0348+0432原生星性质的影响.利用GL85核子耦合参数组计算了PSR J0348+0432的质量,将该参数组推广来计算每重子熵S=1或S=2时原生中子星的性质.结果发现原生中子星较零温中子星会有更多超子出现,且原生中子星的温度越往内部温度越高,超子的出现会降低内部温度.熵会增大大质量原生中子星的质量,这种增加效应超过超子出现减小大质量中子星质量的效应.熵会增加原生中子星的半径,即原生中子星的冷却是一个星体收缩的过程.

宇宙粒子物理,致密物质,状态方程,恒星:演化,恒星:大质量,恒星:中子

1 引言

中子星是已知体积最小、密度最大的星体,提供了超出地球实验室所能够达到的极端物理条件,一直是天体物理、核物理和粒子物理领域研究人员的研究对象.一颗典型中子星的质量大概在1.5倍太阳质量,半径为12 km左右[1].关于典型中子星的质量、半径和状态方程已有大量的研究[2−6].2010年观测到一颗编号为PSR J1614-2230质量为(1.97±0.04)M⊙[7]的大质量中子星,2013年观测到的编号为PSR J0348+0432质量为(2.01±0.04)M⊙[8]的大质量中子星.此类大质量中子星的发现有力地支持组成中子星的物质状态方程的硬化,引起了许多研究人员的兴趣.Miyatsu等人在零温下利用手征夸克介子耦合模型重新构造状态方程,使得构造后的状态方程包含重子八重态,计算得到最大质量为1.95M⊙,与观察到的PSR J1614-2230的质量相符[9].Weissenborn等[10]研究了超子势阱深度对状态方程的影响,发现如果考虑超子间的奇异介子排斥作用,可以计算给出大质量中子星的性质.Zhao等人尝试通过选取一组合理的超子耦合参数去描述大质量中子星PSR J1614-2230[11].中子星都是由原生中子星演化而来的,大质量中子星的原生星的性质对我们了解大质量中子星的性质和演化过程相当重要,但对大质量中子星的原生星性质的研究还相对较少,特别是对2013年观测到的PSR J0348+0432的熵效应还未见报道.

在本文中,我们利用相对论平均场理论考虑重子八重态,研究大质量中子星PSR J0348+0432原生星的组成与结构,我们取每重子熵S=1或S=2[12],主要集中研究中子星的熵效应.

2 有限温度下相对论平均场理论

相对论平均场理论是描述强子相互作用的有效场论[13],其中用标量介子σ、矢量介子ω、同位旋介子ρ去描述核子间的相互作用.σ提供中程吸引力,ω提供短程排斥力,而ρ用来描述质子与中子的区别.

原生中子星是一个热力学系统,对巨正则系综,系统的配分函数为:

式中V为体积.

考虑中子星物质中的重子为Fermi子,介子为Bose子,可以得到:

其中εB(k)和(k)分别代表动量为k的各种重子和反重子能量,L表示系统的拉氏量, µB和ŪB表示重子B和其反重子的化学势,εM(k)表示热激发介子的能量,表示如下:

中子星物质的拉氏量为[13]:

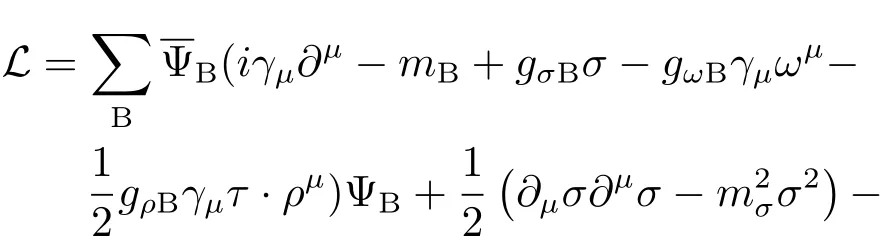
其中m∗=mB−gσBσ代表重子的有效质量.

有限温度下中子星的性质由每重子熵来描述[14],状态方程与每重子熵之间的关系如下式:

其中ρB代表总重子数密度,nB(k)代表动量为k的重子数密度:

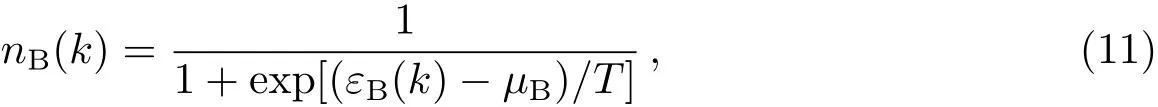
状态方程一旦确定,中子星的性质就可以通过求解Tolman-Oppenheimer-Volko ff方程得到[15]:

3 耦合参数

在相对论平均场理论中,核子-介子耦合参数可以通过饱和核物质密度ρ0,束缚能B/A,压缩系数K,有效质量m∗及对称能系数asym给出[16−17].到目前为止,已经有很多不同的参数组用来计算中子星物质,且都给出了很好的结果[18−20].本文我们选取GL85核子参数组,此参数组能够很好地描述核子之间的相互作用[14],具体数值见表1.

表1 GL85核子耦合参数组Table 1 The coupling constants of the nucleon set GL85

关于中子星中的超子-介子的耦合参数,为了方便起见,定义超子-介子耦合常数与核子-介子耦合常数的比值为:

其中N代表核子,H代表超子.超子耦合参数不能由正常核物质的性质来确定,但是可以通过超核的实验数据对超子耦合常数进行计算.超子H与标量介子σ及矢量介子ω的耦合参数可以根据超子H在核物质中的势阱深度关联起来,在对称均匀核物质中,超子的势阱深度可以表示成:

其中为超子H的势阱深度,S=m−m∗和V=(gω/mω)2ρ0分别为核子饱和密度的标量势和矢量势.实验上给出核物质中Λ、Σ、Ξ超子的势阱深度分别为:

超子耦合参数与核子耦合参数比存在很大的不确定性,有多种取法.比如文献[27]指出,xωH在1/3到1之间,我们不考虑ω介子与超子和核子耦合的区别,即

利用(17)式可计算出σ介子与超子的耦合参数

同位旋ρ介子与超子的耦合参数利用SU(6)夸克对称模型取为:

运用上述耦合参数组,我们基于相对论平均场理论考虑重子八重态计算零温下中子星物质状态方程,计算得到中子星的最大质量为2.10M⊙,计算结果如图1.这个结果与目前观测到的大质量中子星PSR J0348+0432的质量(2.01±0.04)M⊙符合得很好.说明上述参数组可以很好地描述零温大质量中子星物质.

图1 GL85核子参数组和超子耦合参数组xωΛ=xωΣ=xωΞ=1,xσΛ=0.85,xσΣ=0.57,xσΞ=0.78,xρΛ=0,xρΣ=2,xρΞ=1给出的中子星质量随中心能量密度的变化关系.阴影部分代表PSR J0348+0432的质量范围.Fig.1The relation between mass of neutron stars and central energy density with GL85 nucleon coupling parameter sets and hyperon coupling parameter sets which correspond toxωΛ=xωΣ=xωΞ=1,xσΛ=0.85,xσΣ=0.57,xσΞ=0.78,xρΛ=0,xρΣ=2,xρΞ=1.The shaded area corresponds to the mass of PSR J0348+0432.

4 PSR J0348+0432原生星性质的计算结果与讨论

原生中子星是大质量恒星超新星爆发后几秒形成的星体,原生中子星进一步演化会成为稳定的冷中子星.上述的耦合参数组在零温下可以得到大质量中子星PSR J0348+0432的质量,因此我们选取这组参数来计算PSR J0348+0432原生星的性质.计算时我们选取原生星的每重子熵为S=1或S=2,中子星内部除了含有核子外,还有超子Λ、Σ−、Σ0、Σ+、Ξ−、Ξ0.

4.1 粒子数分布

我们首先计算了原生中子星内部各种粒子的数密度,结果如图2所示.图2给出了每重子熵在S=0,S=1和S=2时中子星内部各粒子的相对数密度随总的粒子数密度的分布.从图中可以看出原生中子星内部出现的超子比零温中子星(S=0)内部出现的超子要多,而且熵越大超子出现得越多.

在大质量中子星原生星内部,首先出现的是Λ超子,而后出现Ξ−超子.比如,S=1时中子星内部Λ出现的密度在0.26 fm−3处,S=2时出现的密度在0.12 fm−3处;对于Ξ−超子S=1时在中子星内部出现的密度为0.42 fm−3,S=2时出现的密度为0.24 fm−3,对于零温下的情况(S=0),Λ出现的密度在0.48 fm−3,Ξ−出现的密度在0.71 fm−3,两种超子的出现密度都要比熵不为零的情况下高.

图2 不同熵值情况下,中子星内部各粒子的相对数密度随总粒子数密度的变化Fig.2 Populations of various particles in neutron star matter with the baryon density for di ff erent values of entropy per baryon

在S=0的情况下超子出现的范围在ρ＞0.46 fm−3范围,Σ0和Σ+在我们计算中没有出现,这是因为Σ超子的势阱深度为正值,严重抑制了该种超子在中子星中的生成.S=1时超子出现的范围在0.2 fm−3＜ρ＜0.8 fm−3范围,Σ0和Σ+在图中所示的密度范围内并没有出现.S=2时在0.1 fm−3＜ρ＜0.8 fm−3范围内所有的超子包括Λ、Σ、Ξ全部出现.

上述结果表明,熵有利于超子的产生,而且大质量中子星原生星内部超子要比零温下中子星内部超子多.

4.2 温度

我们计算了原生星内部温度,结果如图3所示.图中可以看出熵越大中子星的温度也越高.如果不考虑超子效应对原生中子星温度的影响,中子星内部的温度将随着密度的增加而不断地升高,对S=1,在密度ρ=0.1 fm−3时温度为8.60 MeV,在ρ=0.9 fm−3时温度上升到39.06 MeV,同样对S=2,温度从20.03 MeV上升到84.37 MeV.

当考虑原生中子星内部含有超子时,由于超子的影响,温度随密度增加明显趋缓.对S=1,在密度ρ=0.1 fm−3时温度为8.60 MeV,在ρ=0.9 fm−3时温度上升到25.49 MeV,同样对S=2,温度从19.98 MeV上升到55.05 MeV.可以看出超子的出现降低了原生中子星内部的温度.

图3 原生中子星内部温度随密度的变化关系.散点代表没有考虑超子,散点加线代表考虑超子.Fig.3 The interior temperature of protoneutron star as a function of the density.The scatters are the calculation results without considering hyperons,while the scatters plus lines are the results with considering hyperons.

4.3 状态方程

状态方程的计算如图4所示,从图中可以看出在考虑超子效应或不考虑超子效应两种情况下,熵越大其状态方程越硬,而超子出现会软化状态方程.

图4 不同熵下压强随能量密度的变化关系.散点代表没有考虑超子,散点加线代表考虑超子.Fig.4 The pressure of neutron star matter as a function of energy density for di ff erent values of entropy per baryon.The scatters are the calculation results without considering hyperons,while the scatters plus lines are the results with considering hyperons.

4.4 质量与半径

利用状态方程,通过求解TOV方程就可以得到大质量原生中子星的质量和半径,结果如图5和图6所示,计算得到的最大质量列于表2中.

图5 不同情况下对应的中子星的质量.散点代表没有考虑超子,散点加线代表考虑超子.阴影部分代表PSR J0348+0432范围.Fig.5 The mass of neutron star for di ff erent cases.The scatters are the calculation results without considering hyperons,while the scatters plus lines are the results with considering hyperons.The shaded area corresponds to the mass of PSR J0348+0432.

图6S=0,1,2条件下质量与半径关系.散点代表没有考虑超子,散点加线代表考虑超子.阴影部分代表PSR J0348+0432的质量范围.Fig.6 Radius-mass relation forS=0,1,and 2 respectively.The scatters are the calculation results without considering hyperons,while the scatters plus lines are the results with considering hyperons.The shaded area corresponds to the mass of PSR J0348+0432.

图5中,如果原生中子星内部不考虑超子,在S=1时的最大质量达到2.16M⊙,S=2时最大质量达到2.21M⊙,对应于冷中子星最大质量为2.14M⊙.这就意味着不考虑超子情况下熵的效应会增加大质量中子星的最大质量.考虑超子出现的原生中子星,S=1时最大质量为2.11M⊙,S=2时为2.12M⊙,零温下中子星最大质量为2.10M⊙,即考虑超子效应时质量都有所减小.但考虑超子效应后熵越大得到的中子星最大质量还是越大.结合原生中子星中超子的相对数密度分布,以上结果表明熵增加大质量中子星质量的效应超过超子出现减小大质量中子星质量的效应.

图6给出了中子星的半径随质量的变化关系.原生中子星半径比冷中子星的半径大,而且熵越大原生中子星的半径也越大.简而言之,原生中子星的冷却过程是一个收缩过程.PSR J0348+0432的原生星在S=2的情况下,考虑超子时得到的半径为15.07 km,不考虑超子时为15.67 km.S=1时,考虑超子时得到的半径为13.71 km,不考虑超子时为13.88 km.而S=0时,考虑超子和不考虑超子时半径分别为12.86 km和12.91 km(这与Antoniadis等人给出大质量中子星PSR J0348+0432的半径范围(13±2)km符合[8]).以上结果说明超子出现会减小大质量原生中子星的半径.

表2 大质量原生中子星的最大质量.εc代表中心能量密度,Pc代表中心压强,Tc表示中心温度,YES代表考虑超子效应,NO代表不考虑超子效应Table 2 The maximum mass of massive protoneutron star.εcis central energy density,Pcis central pressure,Tcis central temperature,and the term YES indicates considering hyperons,NO means unconsidering hyperons.

5 总结

相对论平均场理论框架下,我们考虑中子星内部含超子和不含超子两种情况,选取原生星的每重子熵S=1或S=2.研究了大质量中子星PSR J0348+0432原生星的内部结构和性质.

我们发现大质量原生中子星的内部较冷,中子星内部更容易出现超子,超子的出现会降低中子星内部的温度.熵会增加大质量原生中子星的质量,超子的出现会减小中子星的质量,但熵增加大质量中子星质量的效应会超过超子出现减小大质量中子星质量的效应.大质量原生中子星的半径比冷中子星的半径大,熵越大,原生中子星的半径也越大,简而言之原生中子星的演化过程是一个收缩的过程.

中微子在原生中子星中也起着很重要的作用,我们将在以后的工作中加以讨论.

[1]Lattimer J M,Prakash M.Science,2004,304:536

[2]Cli ff ord E R Jr.,Remo R.PhRvL,1974,32:324

[3]Cooperstein J.PhRvC,1988,37:786

[4]Schulze H J.PhRvC,2006,73:058801

[5]赵先锋.天文学报,2011,52:126

[6]Zhao X F.ChA&A,2011,35:285

[7]Demorest P B,Pennucci T,Ransom S M,et al.Nature,2010,467:1081

[8]Antoniadis J,Freire P C C,Wex N.Science,2013,340:448

[9]Miyatsu T,Yamamuro S,Nakazato K.ApJ,2013,777:4

[10]Weissenborn S,Chatterjee D,Scha ff ner-Bielich J.NuPhA,2012,881:62

[11]Zhao X F,Jia H Y.PhRvC,2012,85:065806

[12]Burrows A,Lattimer J M.ApJ,1986,307:178

[13]Glendenning N K.Compact Star:Nuclear Physics,Particle Physics,and General Relativity.New York:Springer,2000:150-198

[14]Prakash M,Bombaci I,Prakash M,et al.PhR,1997,280:1

[15]Oppenheimer J R,Volko ffG M.PhRv,1939,55:374

[16]贾焕玉,孙宝玺,孟杰,等.天文学报,2002,43:160

[17]Jia H Y,Sun B X,Meng J,et al.ChA&A,2002,26:404

[18]Rufa M,Scha ff ner J,Maruhn J,et al.PhRvC,1990,42:2469

[19]Mareˇs J,Friedman E,Gal A,et al.NuPhA,1995,594:311

[20]Sumiyoshi K,Kuwabara H,Toki H.NuPhA,1995,581:725

[21]Millener D J,Dover C B,Gal A.PhRvC,1988,38:2700

[22]Scha ff ner J,Stoecker H,Greiner C.PhRvC,1992,46:322

[23]Batty C J,Friedman E,Gal A.PhR,1997,287:385

[24]Scha ff ner-Bielich J,Gal A.PhRvC,2000,62:034311

[25]Aoki S,Bahk S Y,Chung K S.PhLB,1995,355:45

[26]Khaustov P,Alburger D E,Barnes P D,et al.PhRvC,2000,61:054603

[27]Glendenning N K,Moszkowski S A.PhRvL,1991,67:2414

Composition and Structure of Massive Protoneutron Star PSR J0348+0432

HONG Bin JIA Huan-yu MU Xue-ling ZHOU Xia
(Institute for Modern Physics,Southwest Jiaotong University,Chengdu 610031)

Considering the octet baryons in relativistic mean fi eld(RMF)theory,the entropy per baryon is selected to be 1 or 2.We investigate the in fl uence of the entropy per baryon for the massive protoneutron star corresponding to PSR J0348+0432.One set of coupling constants GL85 in RMF are selected to reproduce the mass of PSR J0348+0432 at zero temperature,and then extended to describe the massive protoneutron stars with the per baryon entropyS=1 orS=2.It is found that the massive protoneutron stars have more hyperons than the cold neutron stars,the temperature increases with the increase of the density from surface to interior,and the existence of hyperons leads to the decrease of the interior temperature.Entropy causes the increase of the mass of massive protoneutron star,and this e ff ect is more obvious than that of the decreasing mass due to hyperons.The entropy per baryon brings on the increase of the radius of protoneutron star.In other words,the protoneutron star’s cooling may be a contracting process.

astroparticle physics,dense matter,equation of state,stars:evolution, stars:massive,stars:neutron

P145

A

10.15940/j.cnki.0001-5245.2015.06.001

2015-05-10收到原稿,2015-05-22收到修改稿∗国家自然科学基金项目(11175147)资助

†hyjia@home.swjtu.edu.cn