铝合金2A16板材成形极限研究

郭禅,郎利辉,杨希英,刘康宁,张文尚

(北京航空航天大学机械工程及自动化学院,北京100191)

铝合金2A16板材成形极限研究

郭禅,郎利辉,杨希英,刘康宁,张文尚

(北京航空航天大学机械工程及自动化学院,北京100191)

目的 掌握硬铝合金在温热条件下的成形性能变化规律。方法 采用结合半球凸模胀形和椭圆液压胀形的复合试验法进行了FLD试验,用最小二乘法拟合试验数据,建立了成形极限预测模型。结果 试样均在凸模顶端或附近发生破裂,在室温下网格保持较小的圆形,在210℃和300℃下网格被不同程度的拉长和变大,温度对铝合金2A16的成形性能影响很大,随温度升高,成形极限曲线上移。结论 复合胀形试验法具有较高的可靠性与准确性;铝合金2A16在高温下成形性能更好;预测模型较好地表述了极限应变值与温度的关系,根据模型可快速得出FLD。

铝合金;成形极限;椭圆液压胀形;预测模型

出于节能和环保的需求,各种轻量化的新材料被不断使用,尤其在汽车及航空航天制造领域,铝合金等轻质合金的应用十分广泛。在汽车工业中,铝合金主要用来制造壳体类零件和底盘零件,所占比重越来越高[1]。现代飞机的机翼、框等部位均用超高强铝合金制造,火箭主体结构、整流罩等也采用铝合金等轻质合金[2—4]。2系硬铝合金具有韧性和耐热性[5],但常温下成形较为困难,需采用热成形方法。

温度对硬铝合金的成形性能提升较大,为了研究温度对材料成形性能的影响规律,需要进行成形极限研究。研究成形极限的理论方法有很多,如 Swift[6]提出的分散性失稳理论,Hill[7]的集中性失稳理论以及M-K凹槽理论[8—9]。试验方法有刚模胀形、椭圆液压胀形和双向拉伸法。刚性模胀形的加载路径简单,双向拉伸试验能够试验复杂路径加载,北京航空航天大学自主研发了十字形双向拉伸试验机并进行了相关实验[10—12]。针对2系硬铝合金在航空航天中的应用,采用半球凸模胀形和椭圆液压胀形想结合的方法研究其在温热条件下的成形极限,掌握其成形性能对于合理制定材料的工艺流程具有重要的指导意义。

1 椭圆液压胀形试验原理

板材在椭圆液压胀形时,其胀形顶点的微元体如图1所示。设微元面内的主应力分别为σ1,σ2,椭圆长轴与短轴在微元面内形成的曲率半径分别为ρ1, ρ2,微元厚度为t,液压压力为p。对于各向同性材料,椭圆液压胀形顶点应力的计算方法如下:

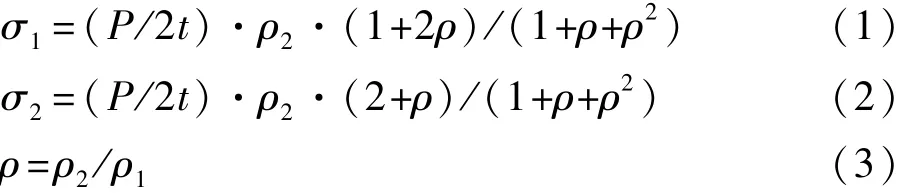
图1 胀形顶点微元体Fig.1 Micro unit of the top bulging part

根据以上公式,利用不同椭圆度x(x=b/a,表示椭圆短轴半径a与长轴半径b长度的比值)的椭圆形凹模液压胀形,能够得到胀形顶点两向主应力关系曲线。改变椭圆凹模的椭圆度,其液压胀形均能保持线性加载,且两向主应力保持线性关系[13—14],不同的椭圆度凹模胀形可得到材料不同的应力状态,且椭圆度x与应力比α之间满足线性关系关系:

式中:m,n分别为与材料有关的常数。在简单加载,且材料各向同性的条件下,极限应变比β与应力比α由如下关系[15]:

因此利用不同椭圆度的凹模进行液压胀形能使材料获得不同的应力状态,根据式(5),不同的应力状态能够对应不同的极限应变状态,因此该方法具备获得不同极限应变状态的条件,可以用来进行成形极限研究。

2 复合FLD试验

2.1 试验材料

试验材料为厚度1.2 mm的硬铝合金2A16。该材料在高温下具有较高的持久强度,在航空航天领域应用广泛,其化学成分(质量分数)如下:Si0.3%,Fe 0.3%,Cu 6.0% ～7.0%,Mn 0.4% ～0.8%,Mg 0.05%,Zn 0.1%,Ti0.1%～0.2%,Zr 0.2%,其他占0.1%,余量为铝。

2.2 半球形凸模胀形试验

用半球形凸模胀形试验获取左半部分极限应变点。试验中所使用的半球形凸模胀形模具尺寸如图2所示。试样长度方向均沿板材轧制方向裁出,长度均为220 mm,宽度分别为20,50,80,110 mm。

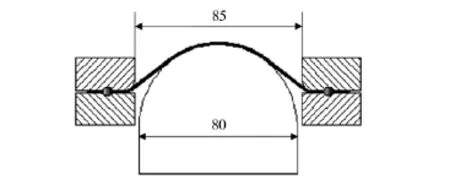
图2 半球形凸模胀形模具尺寸Fig.2 Themold size of rigid punch bulging

试验温度从室温开始,分别为20,210,300℃。为了测定试样的极限应变,需要在试样的一侧板面制取直径为2.5 mm的应变网格圆。室温试验时,试样和凸模之间用油膜润滑,高温试验时,在试样未印制网格的一面喷涂高温润滑剂润滑。图3所示为3个温度下的凸模胀形结果。不同宽度的试件在凸模顶端或者附近发生破裂,试验具有可靠性。图3c为3个温度下试件网格变形,可以看到在室温下网格保持较小的圆形,在210℃和300℃下网格被不同程度的拉长和变大。说明温度对铝合金2A16的成形性能影响很大。

图3 半球形凸模胀形结果Fig.3 The results of rigid punch bulging test

2.3 椭圆液压胀形试验

用椭圆液压胀形试验获取右半部分极限应变点。图4展示的是试验采用的椭圆胀形凹模,其长轴直径均为100 mm,短轴直径依次为40,60,80,100 mm。

图4 不同短轴直径的椭圆液压胀形凹模实物Fig.4 The elliptic dies for hydraulic bulging with differentminor axis diameters

试验温度也设置为20,210,300℃。同样,在试样的一侧板面有效范围内,制取直径为2.5 mm的应变网格圆。椭圆液压胀形结果见图5,由于液压胀形没有摩擦力影响,试样破裂点基本在胀形最高点,通过改变椭圆凹模短轴直径,可得到试样不同的极限应变值,如图5a,通过改变试验温度也可改变试样极限应变值如图5b。

图5 椭圆液压胀形结果Fig.5 The results of elliptic hydraulic bulging test

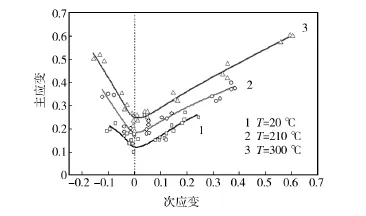
图6 不同温度下2A16板材的成形极限曲线对比Fig.6 The FLCs of 2A16 sheet under different temperatures

2.4 温度对成形极限的影响

试验后对试样进行网格测量和数据处理,得出铝合金2A16的成形极限图,如图6所示。可以看出,温度对铝合金2A16板材成形极限影响十分明显。随着温度提高,板材的极限应变值增大,成形极限曲线整体向上移动这说明,成形的安全区域扩大,板材成形性能提升。在室温下,板材的单拉极限点和双拉极限点对应的应变值较小,当温度升到210℃和300℃时,两个极限点对应的数值增大幅度较大。板材的平面应变点(ε2=0)对应的主应变值也随着温度的提高有较大提升,室温下的极限主应变值为0.142,210℃条件下该值提高到了0.192,300℃条件下该值提高到了0.256。可见,随着温度升高,板材的成形极限平稳上升,高温下板材的成形性能更好。

3 成形极限图预测模型

材料在不同的温度下具有不同的成形极限曲线,一般通过试验方法来获取。而在生产实践中,有时需要尽快知道材料的FLD,需要建立该材料的成形极限预测模型。由于温度对材料成形极限的影响较大,所建立的模型需包含温度影响因子。铝合金2A16板材成形极限预测模型如下所示:

式中:fld0为平面应变状态极限应变点;k1,k2,k3均为与温度T相关的函数。确定这4个参数就能确定该预测模型。使用前述FLD试验的数据点,按照式(6)、式(7)进行最小二乘法拟合,所得参数见表1。

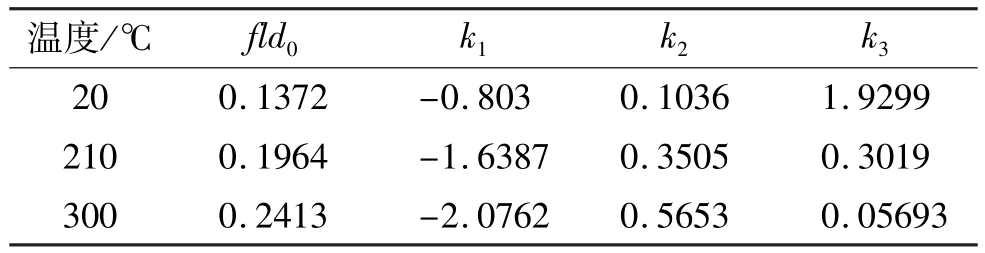
表1 成形极限预测模型参数值Tab le 1 Param eter values of the p red iction m odel of form ing lim it

从表1可以看出,4个参数均为以温度T为自变量的函数,其中fld0,k2随温度的升高而增大,k1,k3随温度的升高而减小。使用二次多项式对4个参数进行拟合,得出他们与温度之间的关系:

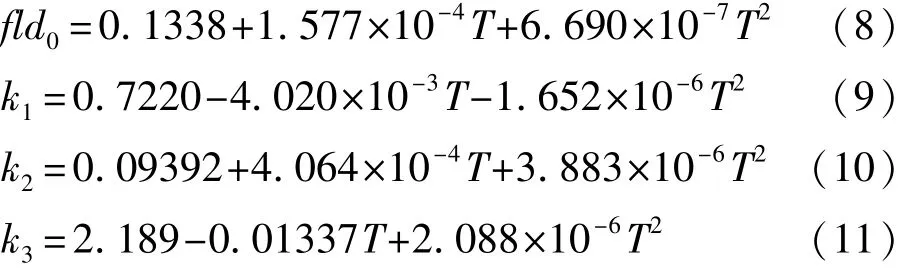
确定模型参数,即确定了铝合金2A16成形极限预测模型,该模型说明了材料主应变、次应变以及温度之间的关系。在工程实际中,给定试材料和试验温度,就可根据预测模型快速得出FLD。

4 结语

1)使用半球凸模胀形和椭圆液压胀形相结合的复合试验方法得出铝合金2A16板材的成形极限图,试验效果良好,该复合方法具有较高的可行性和准确性。

2)温度对铝合金2A16板材成形极限影响十分明显,随着温度提高,板材的成形极限曲线整体向上移动,成形的安全区域扩大,2A16在高温下具有更好的成形性能。

3)对试验数据进行拟合,建立了铝合金2A16成形极限预测模型,确定了模型参数与温度之间的关系,与实际相符,该模型有助于在工程实践中快速得出FLD。

[1]郭玉琴,朱新峰,杨艳,等.汽车轻量化材料及制造工艺研究现状[J].锻压技术,2015,40(3):1—6. GUO Yu-qin,ZHU Xin-feng,YANG Yan,et al.Research State of Lightweight Material and Manufacture Process in Automotive Industry[J].Forging and Stamping Technology, 2015,40(3):1—6.

[2]UNGUREANU C A,DASS,JAWAHIR IS.Life-cycle Cost Analysis:Aluminum versus Steel in Passenger Cars[J]. TMS(The Minerals,Metals&Materials Society),2007: 11—24.

[3]MORDIKE B,EBERT L T.Magnesium Properties-applications-potential[J].JMater Sci Technol,2001,302:37—45.

[4]张钰.铝合金在航天航空中的应用[J].铝加工,2009, (3):50—52. ZHANG Yu.The Application of Aluminum Alloy in Aerospace Field[J].Aluminum Fabrication,2009,(3):50—52.

[5]王建国,王祝堂.航空航天变形铝合金的进展[J].轻合金加工技术,2013,41(8):1—6. WANG Jian-guo,WANG Zhu-tang.Advance on Wrought A-luminum Alloys Used for Aeronautic and Astronautic Industry[J].Light Alloy Fabrication Technology,2013,41(8): 1—6.

[6]SWIFTHW.Plastic Instability under Plane Stress[J].Journal of the Mechanics and Physics of Solid,1952,1(1):1—18.

[7]HILLR.On Discontinuous Plastic Stateswith Special Reference to Localized Necking in Thin Sheets[J].Journalof the Mechanics and Physics of Solid,1952(1):19—30.

[8]马高山,万敏,吴向东.基于M-K模型的铝锂合金热态下成形极限预测[J].中国有色金属学报,2008,18(6): 980—984.

MA Gao-shan,WAN Min,WU Xiang-dong.Theoretical Prediction of FLDs for Al-Li Alloy at Elevated Temperature Based on M-K Model[J].The Chinese Journal of Nonferrous Metals,2008,18(6):980—984.

[9]杜平梅,郎利辉,刘宝胜,等.基于M-K模型的成形极限预测及参数影响[J].塑性工程学报,2011,18(5):84—89. DU Ping-mei,LANG Li-hui,LIU Bao-sheng,et al.Theoretical Prediction and Parameter Influence of FLDs Based on M-K Model[J].Journal of Plasticity Engineering,2011,18 (5):84—89.

[10]万敏,洪强,吴向东,等.十字形试件双向拉伸试验系统建立及加载精度分析[J].机械工程学报,2001,37(1): 57—62. WAN Min,HONG Qiang,WU Xiang-dong,et al.Establishment of Biaxial Tensile Test of Cruciform Specimen and A-nalysis of Load Accuracy[J].Chinese Journal of Mechanical Engineering,2001,37(1):57—62.

[11]舒建,吴向东,王文平,等.温热环境下汽车用钢DP590板材屈服行为[J].塑性工程学报,2015,22(1):66—71. SHU Jian,WU Xiang-dong,WANG Wen-ping,et al.Study on Yield Behavior of Automotive Steel DP590 under Thermal Environment[J].Journal of Plasticity Engineering, 2015,22(1):66-71.

[12]YU Y,WAN M,WU X D,et al.Design of a Cruciform Biaxial Tensile Specimen for Limit Strain Analysis by FEM[J]. Journal of Materials Processing Technology.2002,123(1): 67-70.

[13]李春峰,杨玉英,李雪春.椭圆凹模液压胀形研究[J].电子工艺技术,1995(6):15—18. LIChun-feng,YANG Yu-ying,LI Xue-chun.The Study on Elliptic Dies Hydraulic Bulging[J].Electronics Process Technology,1995(6):15—18.

[14]李春峰,李雪春,杨玉英.椭圆凹模液压胀形法制作成形极限图[J].材料科学与工艺,1996,4(2):101—105. LIChun-feng,LIXue-chun,YANG Yu-ying.Drawing Forming Limit Diagraphs using Elliptic Dies Hydraulic Bulging [J].Materials Science and Technology,1996,4(2):101—105.

[15]REESDW A.Plastic Flow in the Elliptical Bulge Test[J]. International Journal of Mechanical Sciences,1995,37(4): 373—389.

Form ing Lim it of Alum inum Alloy 2A16

GUO Chan,LANG Li-hui,YANG Xi-ying,LIU Kang-ning,ZHANGWen-shang
(School of Mechanical Engineering and Automation,Beihang University,Beijing 100191,China)

This research aimed to learn the changing law of formability of aluminum alloy under warm/hot environment.In this research,the FLD test by amethod combined of rigid punch bulging and hydraulic bulging was conducted, then the predictionmodel of forming limitwas established using the least squaremethod.The results showed that the fracture points were on or near the top of the specimens,the grids remained small under the room temperature while they became bigger and longer under 210℃ and 300℃,indicating the temperature had huge influence on the formability of aluminum alloy 2A16 that the curve of forming limitwas shifted upward with the increase of temperature.The compound bulgingmethod for test had high reliability and accuracy which revealed that aluminum alloy 2A16 had greater formability under high temperatures.The prediction model well described the relationship between the limit stain and the temperature, and FLD can be quickly gained using this predictionmodel.

aluminum alloy;forming limit;elliptic hydraulic bulging;prediction model

10.3969/j.issn.1674-6457.2015.04.016

TG115

:A

:1674-6457(2015)04-0076-04

2015-05-28

国家自然科学基金资助项目(51175024)

郭禅(1989—),男,湖北人,硕士研究生,主要研究方向为板材充液热成形。

郎利辉(1970—),男,河南人,教授,博士生导师,主要研究方向为液压成形、粉末热等静压等塑性成形技术,以及数值模拟、并行工程、CAD/CAM/CAE/CAPP。