设计同等位相异值遗传算法解决一维多峰函数早收敛问题

姚志敏

(广东培正学院 计算机科学与工程系，广州 510830)

遗传算法是解决多峰优化和多模态问题的重要工具，使用遗传算法解决优化问题既存在一定的不确定性，又具有一定的稳定性［1］。但不足的是遗传算法在多峰值函数优化求解过程中往往出现早熟收敛，使群体过早的失去多样性，收敛于局部最优点。曾经出现过许多的改进方法，包括对群体的分类和参数设计，对选择算子、交叉算子和变异算子的改进，试图避免搜索方向收敛于局部最优点，偏离全局最优解的问题。

从遗传算法产生新个体的能力来看，交叉运算是产生新个体的主要方法，它决定了算法的全局搜索能力，而变异运算是产生新个体的辅助方法，但它决定了遗传算法寻找新的搜索方向能力，应当是解决遗传算法早熟收敛重点研究对象。

笔者在遗传算法研究中发现，在种群进化的某一代中，种群中所有位串的某一个等位基因产生相同值，是产生早熟收敛的重要原因。如群体 S:(1001111010101010，1010101001010011，0001010011101010，1010111010111001，… ，0010101010111001)中，第二列值全为0。任何交换算子都是等位交换基因值，群体中任意选择两个个体交换计算后，产生的两个新个体第二列的值依然会保持为0。把具有这种性质的种群称为等位同值群体，在进化中由于模板原理的作用很容易产生等位同值群体，这是造成遗传算法早熟收敛的重要原因。

变异算子可以改变等位同值群体为等位异值群体，由于变异算子并不针对位串的某一位，变异概率pm取值很小，进化中要经过很多代才能确保某位的值发生变异，如上述群体中有位串第二位的值发生变异。若pm取值大，则会破坏已形成的模板规则，使算法不能稳定收敛到结果。

基于以上分析，在算法中注意改变等位同值群体为等位异值群体，是避免遗传算法早熟收敛有效方法。

1 BDGA 算法描述［2］

通过定义等位异值变异算子进行有向导的变异计算，将每一位基因值的差异性在不同代遗传中加以保留，其实质是对某代遗传群体，若某同位基因值全部相同，则主动强制变异使其产生修正，以避免在进化中，有某位基因值缺少差异而导致不能继续进化，从而较好的解决GA 早熟问题。

1.1 编码方式

由于二进制编码方式编码、解码操作简单，而且交叉、变异操作便于实现，故采用二进制编码方式。

1.2 概念定义

令Xn(n 为串的长度)为样板空间，S 表示进化群体，= 1，2，…，L，L，M 为正整数，L ≤2n且M ≤L;，其中

定义1 等位同值群体。

定义2 等位异值群体。

若群体S 不是等位同值群体，则称S 为等位异值群体。

定义3 简单群体［1－3］。

在每一代群体中，每个个体之间的位串结构互不相同。数学描述如下:

遗传算法中的变异算子主要是在保持了群体多样性的基础之上，提高算法的局部搜索能力，但是简单遗传算法中提到的变异操作都是基于变异概率，针对单个个体的突变，这样虽然可以产生新的个体，维持种群的多样性，但是这种操作方式并没有从整个种群(即所有个体)的角度来进行突变，进而维持种群的多样性，基于此，提出等位异值变异算子。

定义4 等位异值变异。

在进化的任一代中，若群体S 是等位同值群体，k 为同值位，进行如下变异操作:以概率pm选择S中的串，使群体S 变成等位异值群体，称此变异为等位异值变异。

下面举例说明，假定群体S1 规模为M=5;串长n =15，并进一步假定在第t 代，群体由下面的串组成。

从上面可以看出:位串在4 号基因位上的值都为1，故S1 为等位同值群体，4 是同值位。在这一代中，交叉算子的作用并不能够使得4 号基因位的值产生变化，按照通常的变异操作，位串在基因位4 产生变异的概率很小，进化中S1 往往保持等位同值群体的性质，使进化陷入了局部最优解而过早的收敛。

为了能够使进化过程突破局部搜索，避免算法的提前收敛，按照给定的变异概率强制其中的某个位串，如X3在同值位4 上发生突变(1 变0)，使S1 成为等位异值群体。这样的变异操作其实是从列的角度进行的变异操作，而通常的变异操作是从行的角度来考虑的。

1.3 BDGA 算法设计［4－5］

下文中提到的变量说明如下。

种群数量:m;迭代次数:k;交叉概率:pc;变异概率:pm;自变量个数:n ;第i 变量编码长度:;第i 变量上下界:;种群中个体串长度L

步骤1——初始化:读取种群的参数信息(m，k，pc，pm，n，li，ai，bi)，初始化种群S，使种群以上述参数提供的信息随机产生一系列二进制串。记S(其中:“xijk”代表0 或者

步骤2——迭代演化:在满足迭代条件下(即迭代次数≤k)，重复执行(1)～(6)。

(1)将m 个长度为L 的二进制串按照个体适应度值由大到小进行排序;

(2)检查新群体是否符合简单群体，若不符合，对种群进行简单化处理，使得种群为简单群体;

(3)查S 是否为等位异值群体，若不是，即对S 中的串Xi=存在某一位xijk或几位，有或者m;那么以概率pm(pm可以取0.1 ～0.2)选择S 中的串xij，使得:

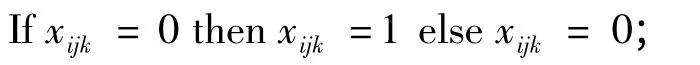
这样生成新串，使群体为等位异值群体;

(4)以交叉概率pc(实际操作中可取pc=0.8)执行交叉操作;将S 中的m 个串随机组成对，采用一点交叉法，随机选择交叉位，对其中的× pc对进行交叉操作;

(5)根据精英保留策略执行选择操作;

(6)返回到(1)继续执行，直到满足最大迭代次数k。

步骤3——结果输出:输出第k 代种群。

2 实证分析［6 －7］

结合简单群体策略和精英保留算法，对多峰连续函数优化问题进行了大量实证研究(实证计算所选4 个函数是经典的GA 测试函数［2］)，获得了很好的结果，对遗传算法的应用具有重要参考价值。

一维(多峰)函数

1)多个极值点、等距、等高f1。

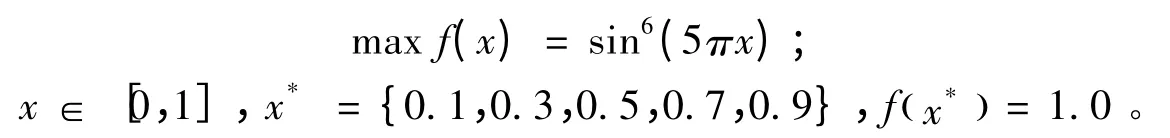
该函数图像如图1 所示。

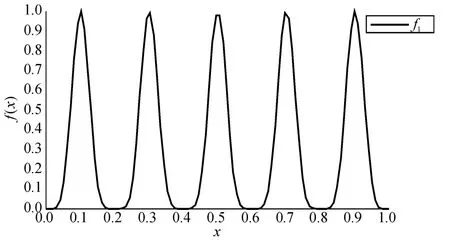
图1 f1 曲线

表1 给出了BDGA 算法对于此函数的计算参数及其结果。

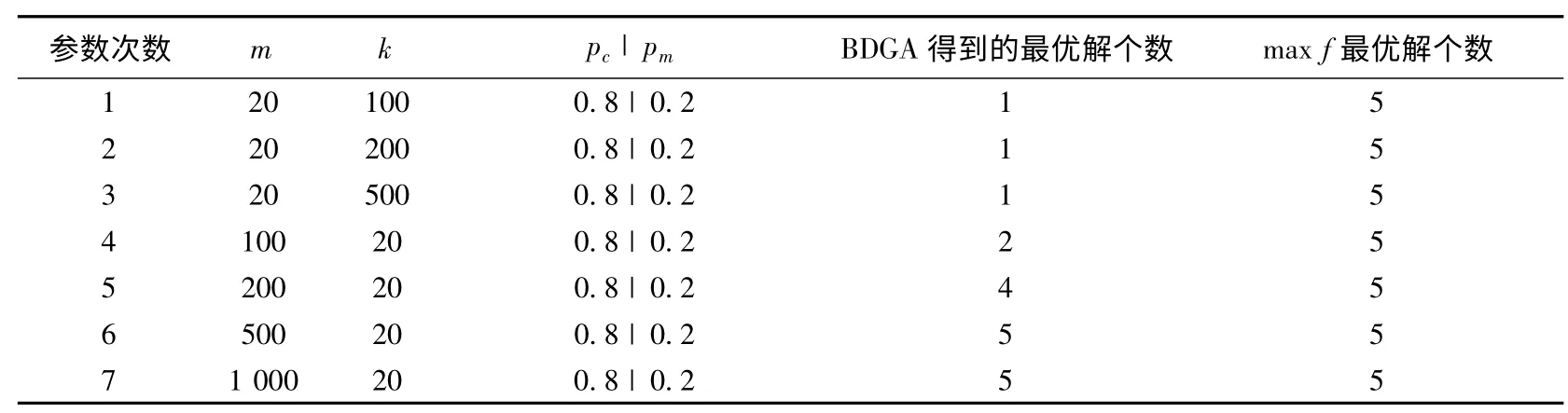
表1 BDGA 算法计算参数及结果

图2 显示了第4 ～7 次计算过程中适应度均值变化情况，从图中可以看出，该算法的收敛效率非常高。

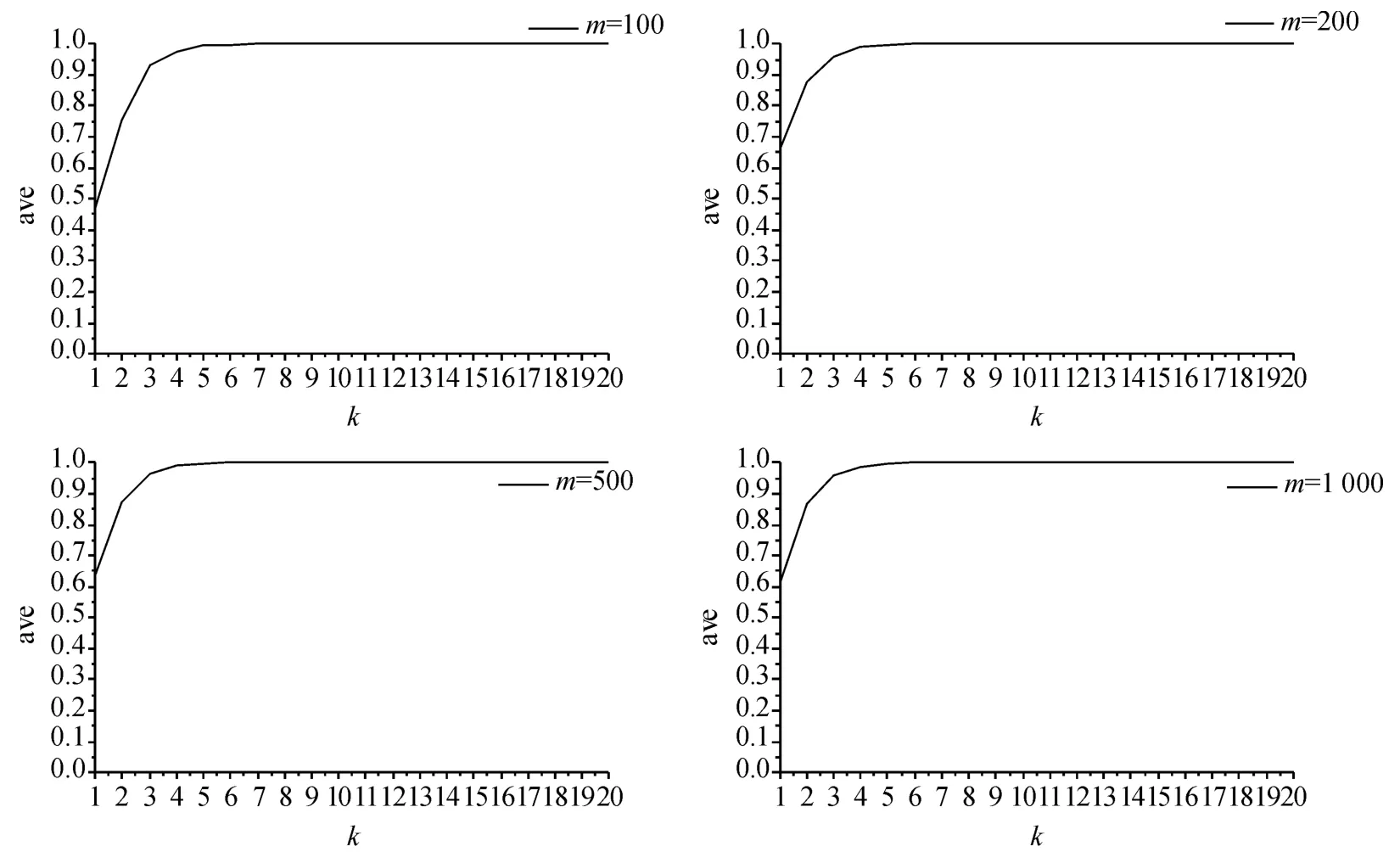
图2 各代适应度均值的变化曲线

由于篇幅有限，在此选取第7 次计算结果文件部分内容显示如图3 所示。

图3 第7 次计算结果文件片段

2)多个极大值点，等距、非等高f2。

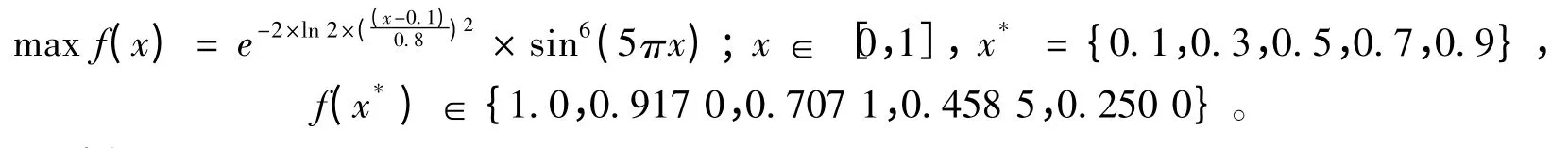
函数曲线如图4 所示。

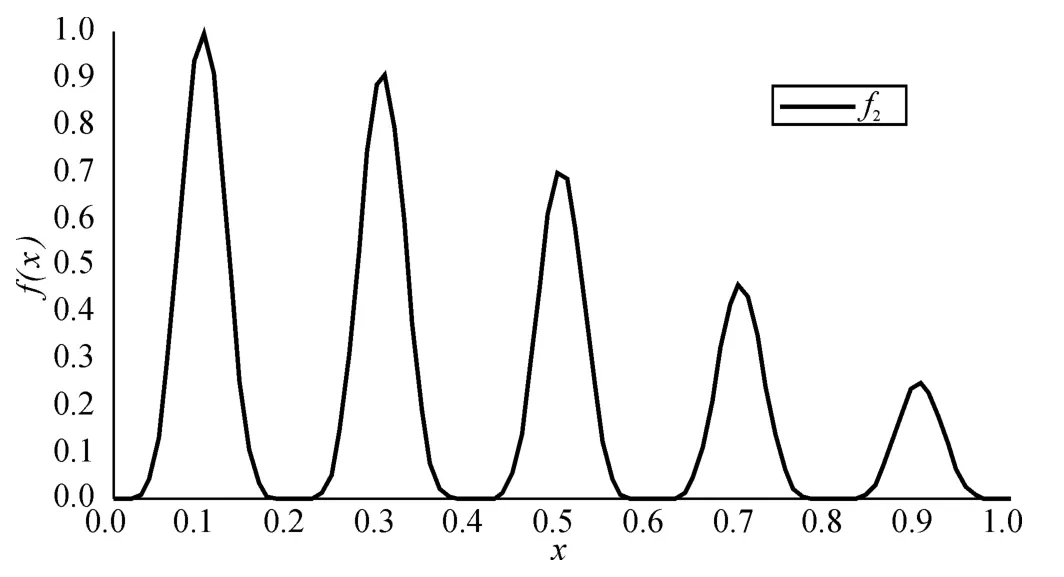
图4 f2 曲线

表2 给出了BDGA 算法对于此函数的计算参数及其结果。

表2 BDGA 算法计算参数及结果

3)多个极大值点，等高，非等距f3。

此函数曲线如图5 所示。

图5 f3 曲线

表3 给出了BDGA 算法对于此函数的计算参数及其结果。

4)多个极大值点，非等高，非等距f4

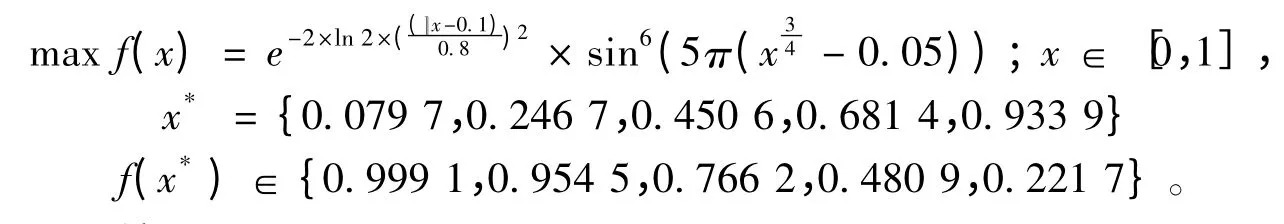
此函数曲线如图6 所示。

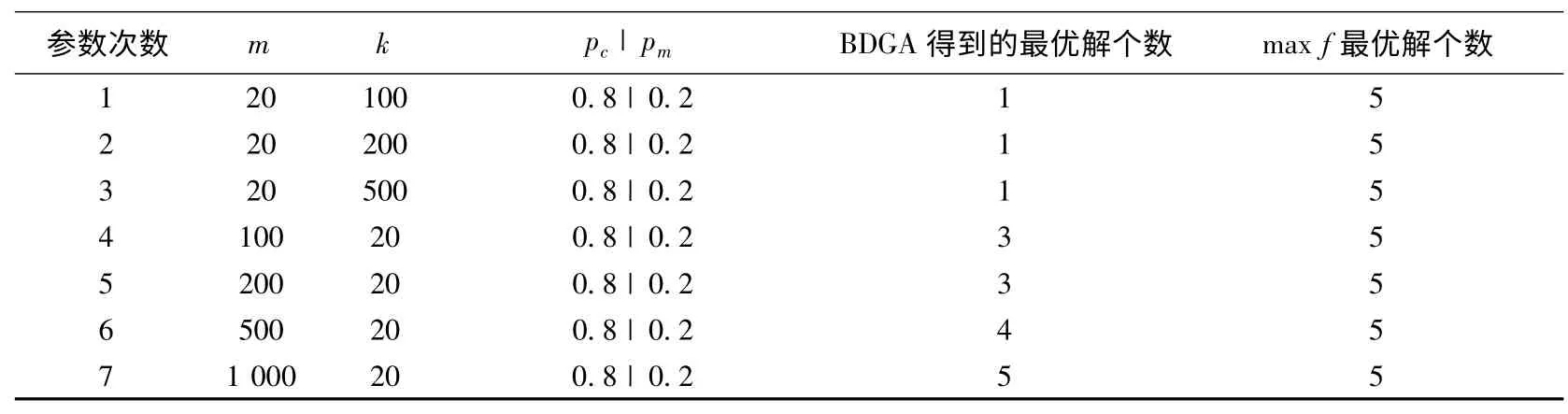
表3 BDGA 算法计算参数及结果

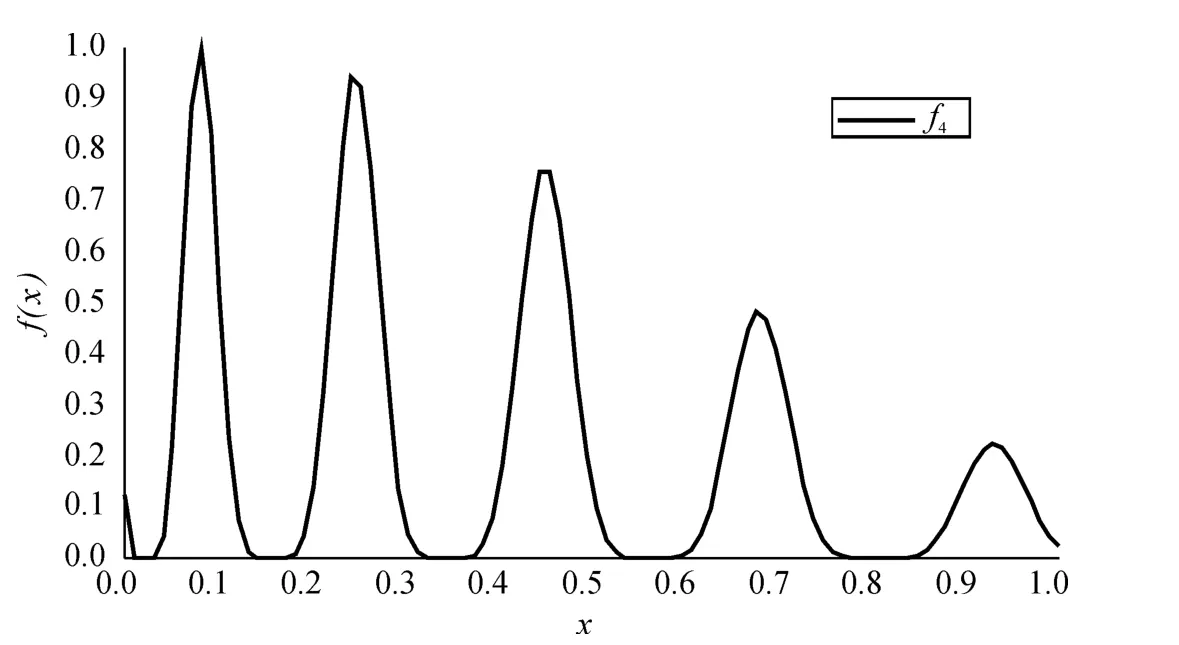
图6 f4 曲线

表4 给出了BDGA 算法对于此函数的计算参数及其结果。

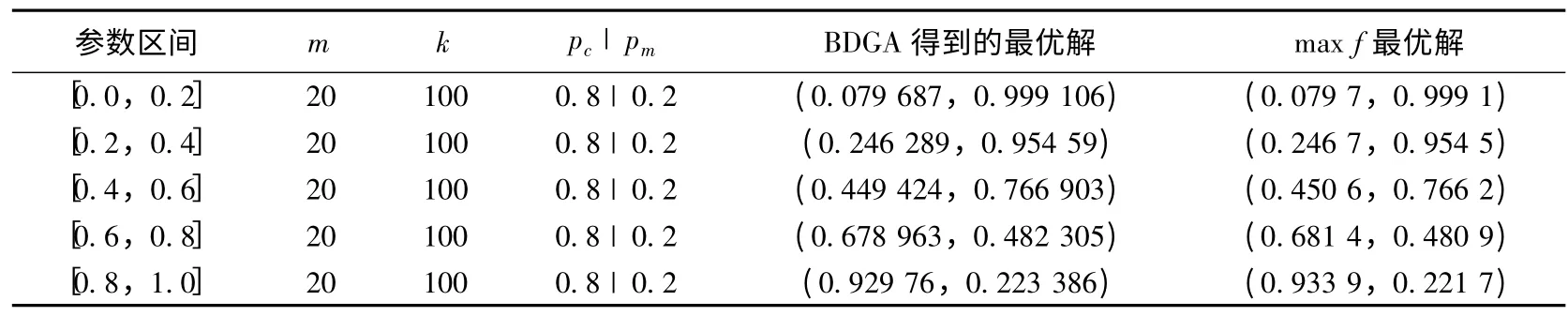
表4 BDGA 算法计算参数及结果

3 结语

研究遗传算法的遗传算子具体操作及其对多峰连续性函数的优化求解，提出了等位同值群体和等位异值变异的概念，将每一位基因值的差异性在不同代遗传中加以保留，其实质是对位串编码的一种修正过程，目的是避免在进化中，有群体缺少差异而导致不能继续进化。

运用等位异值变异遗传算法求一维多峰函数优化问题，数值试验表明改进算法在求解这些问题中的高效与稳定性。对于不同特性的复杂一维测试函数容易局部收敛问题，该算法能够很好的突破局部收敛，从而获得更好的解。

总之，该算法很好的防止了早熟收敛，显示了良好的优化性能，表明此改进算法是有效的，该思想对遗传算法的进一步研究显然有重要参考价值。

作为一种高效并行的全局搜索方法，遗传算法虽有不足，但仍以其特有的算法特点使其在许多实际问题中越来越广泛被应用，随计算机速度的不断增强，遗传算法的研究进展将变得更大、更快。

［1］岳嵚，冯珊.遗传算法的计算性能的统计分析［J］.计算机学报，2010，32(12):2389－2392.

［2］李敏强，寇纪淞，林丹，等.遗传算法的基本理论与应用［M］.北京:科学出版社，2002:179－206.

［3］Minqiang Li，Jisong Kou.Crowding with nearest neighbors replacement for multiple species niching and building blocks preservation in binary multimodal functions optimization［J］.Journal of Heuristics ，2008，14(3):243－270.

［4］Nedim Tutkun.Optimization of multimodal continuous functions using a new crossover for the real－coded genetic algorithms［J］.Expert Systems with Applications，2009(36):8172－8177.

［5］覃柏英. 非线性规划的遗传算法在多峰函数优化中的应用［J］. 广西工学院学报，2013，24(2):25－31.

［6］王利琴，董永峰，顾军华. 改进的精英遗传算法及其在特征选择中的应用［J］. 计算机工程与设计，2014，35(5):1792－1796.

［7］赵婕. 基于VB 的遗传算法在多峰函数全局优化中的应用［J］. 太原大学学报，2014，15(1):128－131.