Dipolar Matter Wave Soliton Modulated by the Optical Lattice

CHEN Gui-hua

(College of Electronic Engineering，Dongguan University of Technology，Dongguan 523808，China)

1 Introduction

Atoms or molecules，which have large magnetic or electric dipoles，namely，dipolar particles，can be oriented by an external field and interact with each other via a long-range dipole-dipole interaction(DDI)［1-2］. The DDI accounts for a number of remarkable phenomena in ultracold Bose gases［3-4］，such as various pattern-formation scenarios［5-7］，fractional domain walls［8］，d-wave collapse［9］，specific possibilities for precision measurements［10-11］，stabilization of the dipolar Bose-Einstein condensates(BECs)by optical lattices［12］，the Einstein-de Haas effect［13］，etc. Dipolar BECs with an attractive or repulsive DDI，which can be controlled by external fields，are generally described by the Gross-Pitaevskii equation(GPE)with nonlocal nonlinearities. Unlike the short-range isotropic interaction between the atoms induced by s-wave scattering，the long-range DDI between dipolar particles exhibits nonlocal and anisotropic characteristics. These features are important for the formation of unidimensional or multidimensional solitons in discrete or continuous systems［14-18］，pattern formation［5，19］，dynamical collapses［9］，and quantum information processes［20］in BECs. Moreover，nonlocality also plays important roles in many other branches of physics，such as the heating and ionization of plasmas［21］and nematic liquid crystals with long-range molecular interactions［22］. All of these make BECs with dipole-dipole interactions an active research subject and useful in potential applications.

In this work，we consider dipolar condensates trapped in a one-dimensional(1D)optical lattice. The orientation of the dipoles is directed by a rotatable uniform external field，and has an intersection angle with the elongation of the 1D lattice，which gives rise to a uniform intersection angle θ. This angle determines the strength of the DDI among condensates，which means that the strength of the nonlocal nonlinearity can be tuned via θ. In contract，the strength of the local nonlinearity is controlled by a magnetic or optical field via the Feshbach resonance［23］. The objective of this work is to study the effect of the trap potential and defect on the formation of dipolar matter-wave solitons in the lattice. In Sect. 2，we give a theoretical description of our model. Numerical studies of formation of the solitons are presented in Sect. 3. The conclusions of this work are given in Sect. 4.

2 The Model

The DDI between two dipole moments located at positions r1and r2is generally given as in Ref.［24］as follows

where d1，2represents the dipole moments of the atoms at positions r1，2satisfying r12=| r12|≡| r1－r2| .=r12/r12，and Cdd= 1/4πε0and μ0/4π corresponding to the cases of the electric and magnetic dipole moments，respectively.

In our model，electric dipole moments are considered. All the dipole moments are induced with the same intensity and oriented in the same direction(as shown in Fig. 1). It results in d1·d2= d2and(d1·)(d2·)= d2cos2θ，where d is the magnitude of the electric dipole moment. The three-dimensional(3D)GPE，which includes both contact and dipole-dipole interactions，reads［25-28］

Figure 1 Dipolar condensates are trapped in a pipe-shaped potential well，whose transverse diameter is indicated by ε.The red arrows point out the direction of the dipole moment and the cosine curve shows a periodically modulated optical field

where U(r)is an arbitrary trap potential contributed by the optical lattice，and asis the s-wave scattering length of the atoms. The condensate is selfrepulsive when as＞0 and self-attractive when as＜0 ，which can be controlled by Feshbach resonance. And we scale the units to fix d2Cdd= 1 . In order to reduce the dimension of the system，an appropriate pipe-shaped potential well(or a cigar shaped potential)is introduced，which is illuminated by a periodically modulated optical field. Under this circumstance，Eq. 2 can be reduced by the underlying 1D nonlocally nonlinear Schrödinger equation in scaled form［14］:

where V(x)=－V0cos(2kxx)，the corresponding 1D form of U(r)，which is the linear potential contributed by the optical lattice，with kxbeing the period of the lattice. σ represents the local interaction(repulsive in the case of σ ＞0 ). To focus on the effect dominated by the DDI，we will drop the local nonlinearity by setting σ =0(in the experiment this can be done by means of the Feshbach resonance［29］). The integrand of Eq. 3，which accounts for the DDIs in the pipe，is regularized by the transverse diameter ε，which is an approximation sufficient for producing 1D solitons. In the following simulations，we fix ε ≡1 .

In the following sections，we carry out numerical studies to investigate the effect of the trap potential and defect on the formation of dipolar matter-wave solitons in the lattice based on Eq. 3.

3 Numerical Results

In our simulations，solitons are characterized by the total norm，i.e. the number of atoms in a condensate(or the total power in the context of optics)，which is defined as

Stationary solutions to Eq. 3 with chemical potential μ are sought in the conventional form ψ(x，t)=u(x)exp(－iμt)with a real function u(x). The numerical process is carried out by the imaginary-time propagation(ITP)method［30-31］. Here，we apply the periodic boundary condition as our numerical boundary condition.To focus on the effects of the trap potential and the defect，we fix the angle θ to be zero. Not only fundamental solitons but also odd solitons are found. Typical examples of two kinds of soliton solutions are shown in Fig. 2.Direct simulations are adopted to examine the stability of these solutions. The evolutions of the solitons with V0=1.0 is shown in Fig. 2(b)and Fig. 2(d). Both the fundamental solitons and odd solitons can exist stably in the middle of the lattice. The shape of both types of solitons changes with the amplitude of trap potential V0［As shown in Fig. 2(a)and Fig. 2(c)］. A deeper potential leads to a sharper profile of the solitons.

Figure 2 The profiles and evolutions of fundamental and odd solitons

To show the stability of the solitons，numerical simulation is carried out to address the relation between the chemical potential μ and the amplitude of the trap potential V0. Chemical potential of the system deceases almost linearly as the amplitude of the trap potential increases，and larger condensate(total norm P)results in a smaller chemical potential［see in Fig.(3)］. It means that the increase of both the atom number of the system and the amplitude of the trap potential can stabilize the solitons.

As mentioned above，the shape of the soliton changes with the amplitude of trap potential V0. In order to show the relation quantitatively，we define the full width at half maximum(FWHM)and the average width(AW)of the solitons as

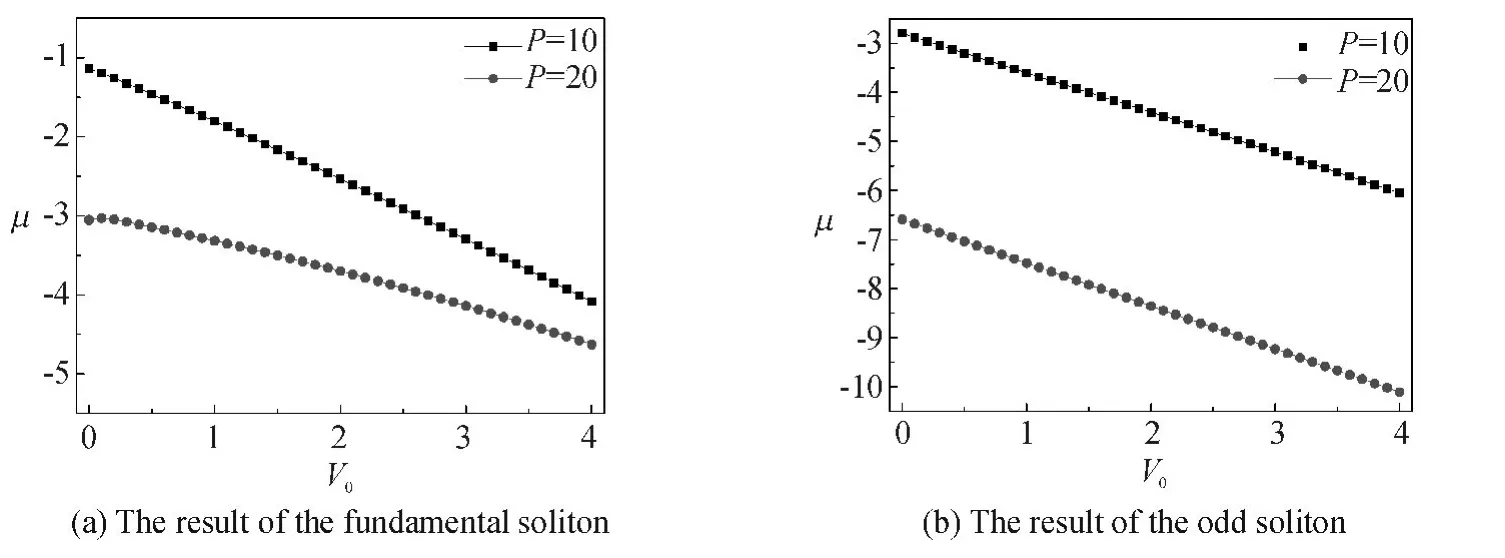
Figure 3 The relation between the chem ical potential μ and the amplitude of the trap potential V0

where u(x)is the stationary solution of Eq. 3，and Lxis the length of the lattice in a period. The relations between FWHM and the amplitude of the trap potential V0are shown in Fig. 4(a)and 4(c)，while the relations between AW and V0are displayed in Fig. 4(b)and 4(d). All of these results indicate that the width of both the fundamental soliton and odd soliton decreases rapidly as the amplitude of the trap potential increases，and tends to a constant width when the amplitude exceeds a certain threshold.

Figure 4 The relations between FWHM/AW and V0 in two kinds of solitons

We also consider the case in which a defect is introduced in the middle of the lattice. We choose the form of the defect as

where Vd0is the amplitude of the defect. We find that solitons can also exist stably in the system with defect. Fig.5(a)shows two typical examples of solitons in the conditions Vd0= 1.0 and 2.0 ，in which the trap potential is fixed to V0= 1.0 . Solitons are dispersed from the middle of the lattice by the defect when Vd0is large enough.There exists a threshold amplitude of the defect Vdc，above which solitons are dispersed from the middle. In order to identify this threshold，relation curves of the chemical potential μ，average width(AW)，and barycenter(Xmc)depending upon Vd0are worked out in Fig.5(b)，5(c)，and 5(d)，respectively. The barycenter Xmcof the soliton is defined as

Figure 5 The effect of defect on the fundamental solitons

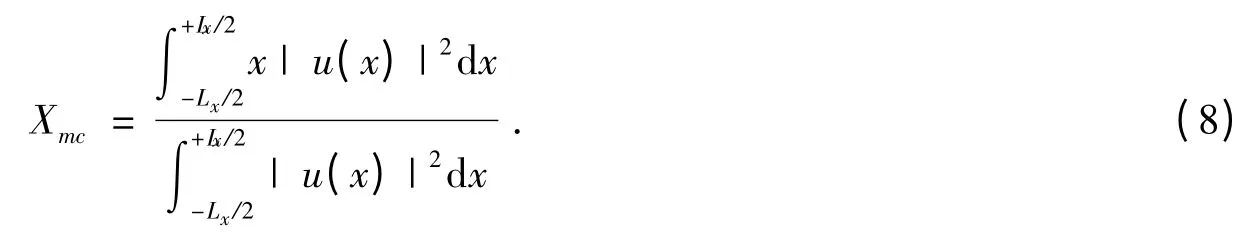
In these figures，we can distinguish obviously that Vdc= 2.7 as V0= 1.0 ，and Vdc= 3.6 when V0= 2.0 . However，the barycenter Xmcis unaffected by V0，as Fig. 5(f)indicated，where the barycenter of the soliton locates at the middle of the lattice when Vd＜Vdc，and dispersed to X ～3 when Vdexceeds Vdcno matter which value V0takes. The influence of V0on Vdcand Xmcis shown in Fig. 6. The result clearly points out that there is no relation between Xmcand V0. And when V0increases，Vdcascends at a decreasing rate.

Figure 6 The influence of V0 on Vdc and Xm c

4 Conclusion

The objective of this work is to study the effect of the trap potential and defect on the formation of dipolar matter-wave solitons in a 1D optical lattice. The numerical simulation is carried out by the imaginary-time propagation method. Not only fundamental solitons，but also odd solitons can exist stably in the middle of the lattice，and their shapes change with the amplitude of trap potential. The width of both the fundamental soliton and odd soliton decreases rapidly as the amplitude of the trap potential increases，and tends to be a constant when the amplitude exceeds a certain threshold. The chemical potential of the matter-wave soliton is calculated and the relation of the chemical potential with the amplitude of the trap potential is figured out. The increase of both the atom number of the system and the amplitude of the trap potential can stabilize solitons. The influence of a defect on fundamental soliton is also considered. When the defect is introduced in the middle of the lattice，fundamental soliton is dispersed from the center as the amplitude of the defect is large enough. The threshold amplitude of the defect to disperse the soliton is obtained. It is found that the threshold is related to the amplitude of the trap potential. With the increasing of the trap potential V0，the threshold ascends at a decreasing rate.

［1］Lahaye T，Menotti C，Santos L，et al. The Physics of Dipolar Bosonic Quantum Gases［J］. Reports on Progress in Physics，2009，72(12):126401.

［2］Baranov M. Theoretical Progress in Many-Body Physics with Ultracold Dipolar Gases［J］. Physics Reports，2008，464:71 –111.

［3］Griesmaier A，Werner J，Hensler S. Bose-Einstein condensation of chromium［J］. Physical Review Letters，2005，94:160401.

［4］Kawaguchi Y，Saito H，Ueda M. Einstein-de Haas Effect in Dipolar Bose-Einstein Condensates［J］. Physical Review Letters，2006，96:080405.

［5］Saito H，Kawaguchi Y，Ueda M. Ferrofluidity in a Two-Component Dipolar Bose-Einstein Condensate［J］. Physical Review Letters，2009，102:230403.

［6］Maluckov A，Gligoriс＇G，Hadžievski L，et al. Stable Periodic Density Waves in Dipolar Bose-Einstein Condensates Trapped in Optical Lattices［J］. Physical Review Letters，2012，108:140402.

［7］Łakomy K，Nath R，Santos L. Faraday Patterns in Coupled One Dimensional Dipolar Condensates［J］. Physical Review A，2012，86:023620.

［8］Wikberg E，Larson J，Bergholtz E，et al. Fractional Domain Walls From On-Site Softening in Dipolar Bosons［J］. Physical Review A，2012，85:033607.

［9］Lahaye T，Metz J，Fröhlich B，et al. d-Wave Collapse and Explosion of a Dipolar Bose-Einstein Condensate［J］. Physical Review Letters，2008，101:080401.

［10］Vengalattore M，Leslie S，Guzman J，et al. Spontaneously Modulated Spin Textures in a Dipolar Spinor Bose - Einstein Condensate［J］.Physical Review Letters，2008，100:170403.

［11］Fattori M，Roati G，Deissler B，et al. Magnetic Dipolar Interaction in a Bose-Einstein Condensate Atomic Interferometer［J］. Physical Review Letters，2008，101:190405.

［12］Müller S，Billy J，Henn E，et al. Stability of a Dipolar Bose-Einstein Condensate in a One-Dimensional Lattice［J］. Physical Review A，2011，84:053601.

［13］Gawryluk K，Bongs K，Brewczyk M. How to Observe Dipolar Effects in Spinor Bose-Einstein Condensates［J］. Physical Review Letters，2011，106:140403.

［14］Li Y，Liu J，Pang W，et al. Symmetry Breaking in Dipolar Matter-Wave Solitons in Dual-Core Couplers［J］. Physical Review A，2013，87:013604.

［15］Gligoriс＇G，Maluckov A，Stepiс＇M，et al. Two Dimensional Discrete Solitons in Dipolar Bose-Einstein Condensates［J］. Physical Review A，2010，81:013633.

［16］Pedri P，Santos L. Two-Dimensional Bright Solitons in Dipolar Bose-Einstein Condensate［J］. Physical Review Letters，2005，95:200404.

［17］Tikhonenkov I，Malomed B，Vardi A. Anisotropic Solitons in Dipolar Bose-Einstein Condensates［J］. Physical Review Letters，2008，100:090406.

［18］Sakaguchi H，Malomed B. Suppression of Quantum Collapse in an Anisotropic Gas of Dipolar Bosons［J］. Physical Review A，2011，84:033616.

［19］Richter R，Barashenkov I. Two-Dimensional Solitons on the Surface of Magnetic Fluids［J］. Physical Review Letters，2005，94:184503.

［20］Saffman M，Walker T，lmer K. Quantum Information with Rydberg Atoms［J］. Reviews of Modern Physics，2010，82:2313.

［21］Litvak A，Mironov V，Fraiman G，et al. Thermal Selfinteraction of Wave Beams in a Plasma with Nonlocal Nonlinearity［J］. Soviet Journal of Plasma Physics，1975，1:60.

［22］Peccianti M，Conti C，Assanto G，et al. Routing of Anisotropic Spatial Solitons and Modulational Instability in Liquid Crystals［J］. Nature，2004，432:733.

［23］Inouye S，Andrews M，Stenger J，et al. Observation of Feshbach Resonances in a Bose-Einstein Condensate［J］. Nature，1998，392:151.

［24］Kawaguchi Y，Ueda M. Spinor Bose-Einstein Condensates［J］. Physics Reports，2012，520:253.

［25］Morsch O，Oberthaler M. Dynamics of Bose-Einstein Condensates in Optical Lattices［J］. Reviews of Modern Physics，2006，78:179.

［26］Muruganandam P，Adhikari S. Numerical and Variational Solutions of the Dipolar Gross-Pitaevskii Qquation in Reduced Dimensions［J］. Laser Physics，2012，22:813 –820.

［27］Salasnich L，Parola A，Reatto L. Effective Wave Equations for the Dynamics of Cigar-Shaped and Disk-Shaped Bose Condensates［J］. Physical Review A，2002，65:043614.

［28］Gligoriс＇G，Maluckov A，Hadžievski L，et al. Bright Solitons in the One-Dimensional Discrete Gross-Pitaevskii Equation with Dipole-Dipole Interactions［J］. Physical Review A，2008，78:063615.

［29］Lahaye T，Koch T，Froehlich B，et al. Strong Dipolar Effects in a Quantum Ferrofluid［J］. Nature，2007，448:672 –675.

［30］Chiofalo M，Succi S，Tosi M. Ground State of Trapped Interacting Bose-Einstein Condensates by an Explicit Imaginary-Time Algorithm［J］.Physical Review E，2000，62:7438.

［31］Li Y，Pang W，Chen Y，et al. Defect-Mediated Discrete Solitons in Optically Induced Photorefractive Lattices［J］. Physical Review A，2009，80:043824.